随机梯度下降算法 入门介绍（最通俗易懂）

1.什么是梯度

首先给出高数课程中梯度的定义：

如果对上面的定义没有理解也没有关系，用通俗的语言来说，梯度实际上就是一个向量，向量中的各个元素表示多元函数在某一个点对于其中一个自变量的偏导数。

例如，给出一个函数：f(x)=ln(x²+y²+z²)，求出该函数在点(1,2,-2)处的梯度，计算过程如下：

1. 计算在该点处函数f(x)对于变量x、y、z的偏导数。计算出的结果分别为2/9，4/9和-4/9。
2. 对偏导数进行拼接，所以该函数在该点的梯度为(2/9，4/9，-4/9）。

2.什么是梯度下降算法

梯度下降算法是一种对损失函数进行优化来得到使得损失函数值最小的机器学习模型的一种算法。也就是说，梯度下降算法是一种用来在机器学习中求解最佳模型的算法。

这么说可能还不是特别好理解，我们从简单的开始，先介绍梯度下降算法的退化版“斜率下降算法”。

假设一个函数的图像如下图所示，在无法直接到达最低点的情况下，如何计算出函数的最小值？

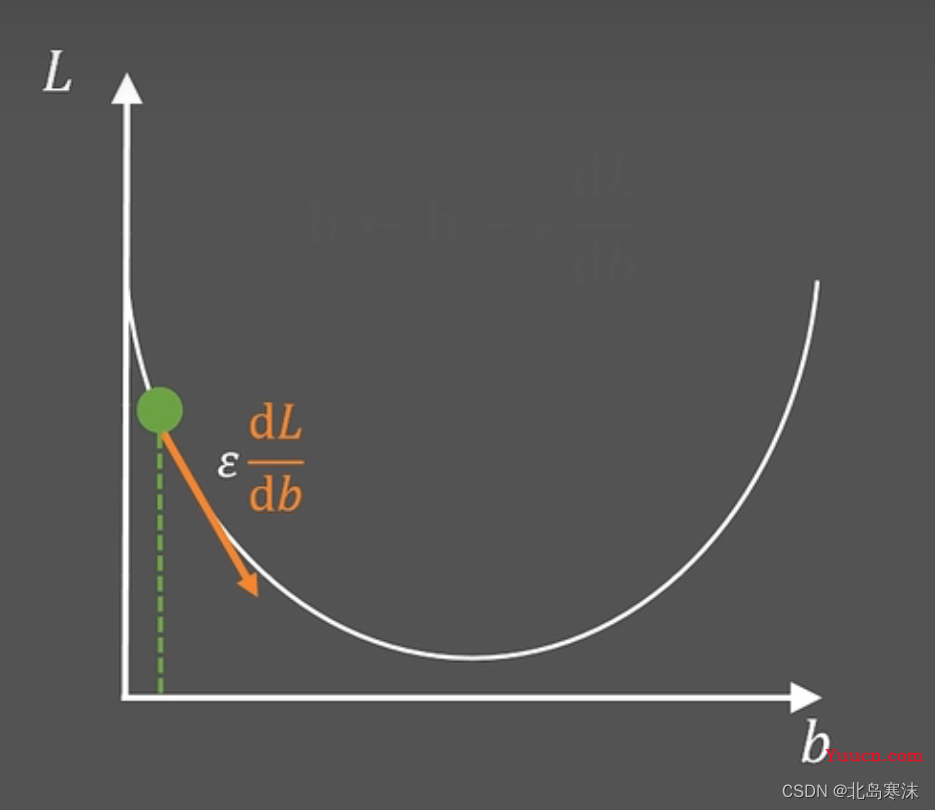
首先需要考虑前进的方向。

假设这样一种情形。当你在一次爬山过程中突然起了大雾，此时想下山的你已经看不清下山的路应该往什么方向走，只能看清眼前很近距离内的路，你应该怎么办才能尽可能地走到山脚？

这时你可以采取这样一种措施：观察眼前的路，如果是下坡路就顺着向下走，走一段距离后再进行一次相同的判断。这样循环往复，你最有可能顺着下坡路成功下山。如果走到一个地方后没有下坡路而是平路了，那么此时你就可以认为自己已经到山脚了。

如果你能够理解上面下山的过程，那么你就明白了梯度下降算法的本质原理。损失函数相当于一座山，而损失函数的最小值相当于山脚，也就是山高度最低的地方，求出损失函数的最小值的过程就相当于从山上的某个地方开始找到下山的路。

假设我们的起点在上图中绿色点标记处，为了能向下走，我们需要判断下坡的方向。而在函数图像中，可以通过斜率判断下坡的方向，因为斜率为负数的方向函数值会减小，也就是我们要走的方向，所以本题中首先需要确定：为了找到最小值，我们需要向右走，也就是增大b值。

我们确定了前进的方向之后，那就得判断再下一次判断之前，我们要在这个方向走多远。

同样可以这么考虑：下坡路越陡，我们越有把握认为这条路可以走到山脚，因此可以一次性沿着这条路走得更远；相对应的，如果下坡路很平缓，我们就会对这条路是否是通往山脚产生一定的怀疑，因此在下一次判断之前，并不会沿着这条路走太远。

在函数上也是这样体现：如果该点下降方向的斜率绝对值大，那么我们一次就会移动得多一点；如果该点下降方向的斜率绝对值小，那么我们一次就会移动少一点。

为了方便控制下坡的速度，我们还需要引入学习率这个变量。

学习率可以这样理解：学习率大，相当于我们是大跨步下山的；学习率小，相当于我们是一步一步挪下山的。

学习率不是一个自动生成的值，需要手动进行设置。类似于下山的人需要自行决定是大步走还是小步走。

通过上面的分析，我们可以得出更新坐标b的公式：

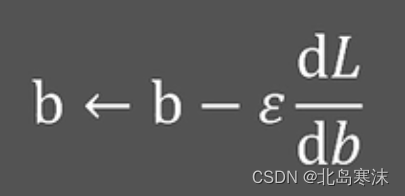
对上面的公式进行几点解释：

• 普适性：无论当前点斜率是正数还是负数，上面的公式都成立。
• 步长控制：步长由当前点的斜率和学习率共同确定。

上面的算法过程，就可以认为是梯度下降算法的退化版“斜率下降算法”。梯度下降算法的过程与“斜率下降算法”完全类似，只不过对于每一个维度（也就是函数中的每一个自变量）都进行一次上面的过程。

相当于下山的过程中，你不仅要考虑向前还是向后是下坡路，同时还要考虑向左还是向右是下坡路，因为最后你走的方向可能是左前方、右后方等而不是直接向着一个单一方向。

上述所述的情况都是针对一个样本点而言对其损失函数进行梯度下降求解，但是实际应用中并非使用损失函数，而是求解使得损失函数在各个样本点的梯度平均值函数值最小的模型参数。损失函数在各个样本点的梯度平均值函数被称为风险函数。

3.什么是随机梯度下降算法

上面我们已经说过，传统梯度下降算法（也称为批量梯度下降算法）中每一次进行判断时都需要计算损失函数在各个样本点的梯度平均值，由此可以得出：

当样本点个数很多时，梯度下降算法逐一的计算过程会耗费大量时间。

同时，这么多的计算结果，如果需要全部保存下来，那么占用的存储空间也是很大的。

因此，对批量梯度下降算法进行改进就得到了随机梯度下降算法。

随机梯度下降算法和批量梯度下降算法的区别在于：随机梯度算法每次只使用少数几个样本点（每次不重复）的梯度的平均值就更新一次模型；而批量梯度下降算法需要使用所有样本点的梯度的平均值更新模型。

因此，随机梯度下降算法的效率明显提高，目前已经得到了广泛应用。