文章目录
- 一、旅行商问题(Traveling Saleman Problem,TSP)
-
- 1.旅行商问题的定义
- 2.旅行商问题求解的计算量
- 二、TSP问题的建模
-
- 1.总体Hamilton量
H
H
H - 2.约束条件
- 3.目标函数
- 1.总体Hamilton量
- 总结
一、旅行商问题(Traveling Saleman Problem,TSP)
1.旅行商问题的定义
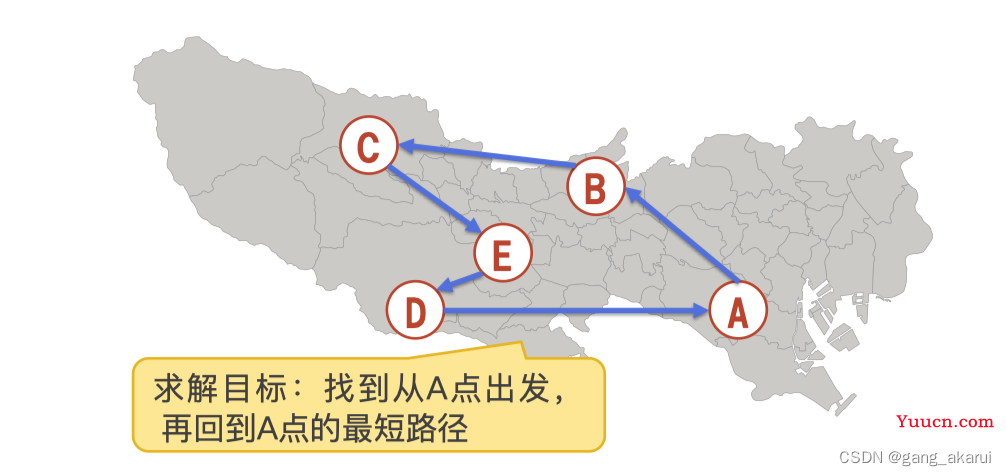
旅行商问题,是一个经典的组合优化问题,而且是著名NP问题之一。如下图所示
,可以想象,有A,B,C,D,E 五个地点,我们想找到一条路径,从地点A出发,经过剩余四个地点,然后回到地点A,从所有可能路径中找到距离最短的一条路径。本章借用了文献[*1]的图表。
2.旅行商问题求解的计算量
最简单的求解方式就是,如下图所示把所有的求解路径全部计算一遍,然后算出每条路径的长度,求出最短路径。
如下图所示,所有的枚举路径总共有24条,我们可以很快找到最短路径。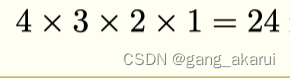

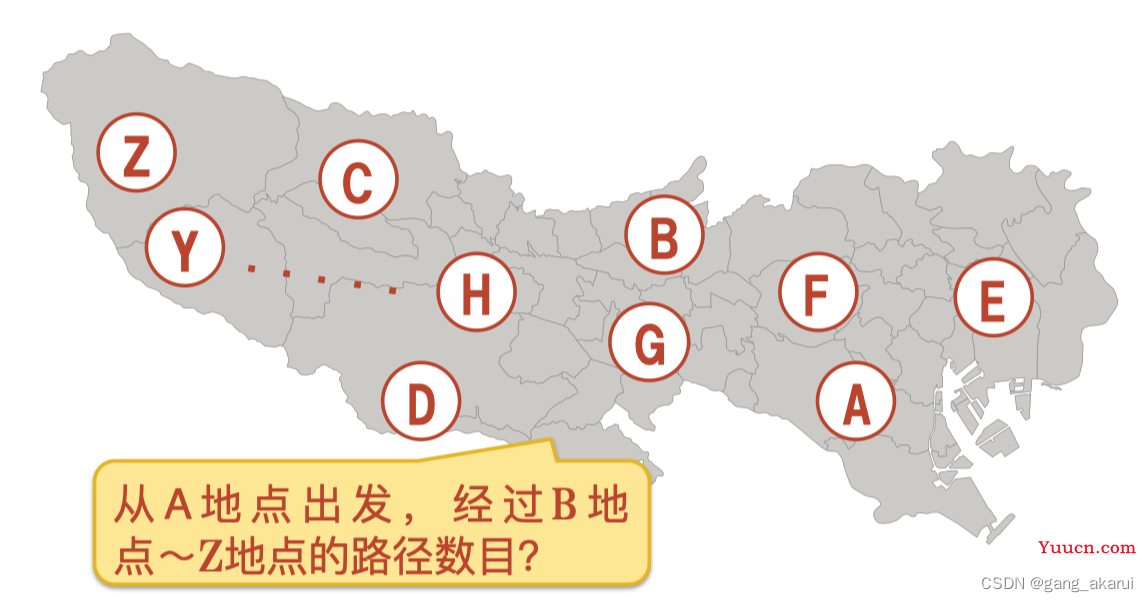
如果下面A~Z的情况,这个计算量,日本的第一超级计算机富岳,每秒的计算速度约为44.2京次(京是10的16次方,即万兆)。一年的秒数是3600×24×365=3153.6万秒。有兴趣的可以计算一下要算多少年。

二、TSP问题的建模
1.总体Hamilton量
H
H
H
该问题输入有两个,这里借用了文章[*2]的图表:
- 地点数目:
N
N
N - 地点之间的距离:
l
i
,
j
(
i
=
1
,
・・・
,
N
)
l_{i,j}(i = 1,・・・, N)
li,j(i=1,・・・,N)
约束条件:
- 每个时间步只能访问一个地点。
- 每个地点都访问过一次。
整体的Hamilton量
H
H
H如下:


目标变量
x
i
,
j
x_{i,j}
xi,j的两个下标的意思如下图👇所示,绿色的圆圈代表在某个时间步访问了某个第地点,所以我们的目标变量就可以用0或1表示了,0代表未访问,1代表访问。
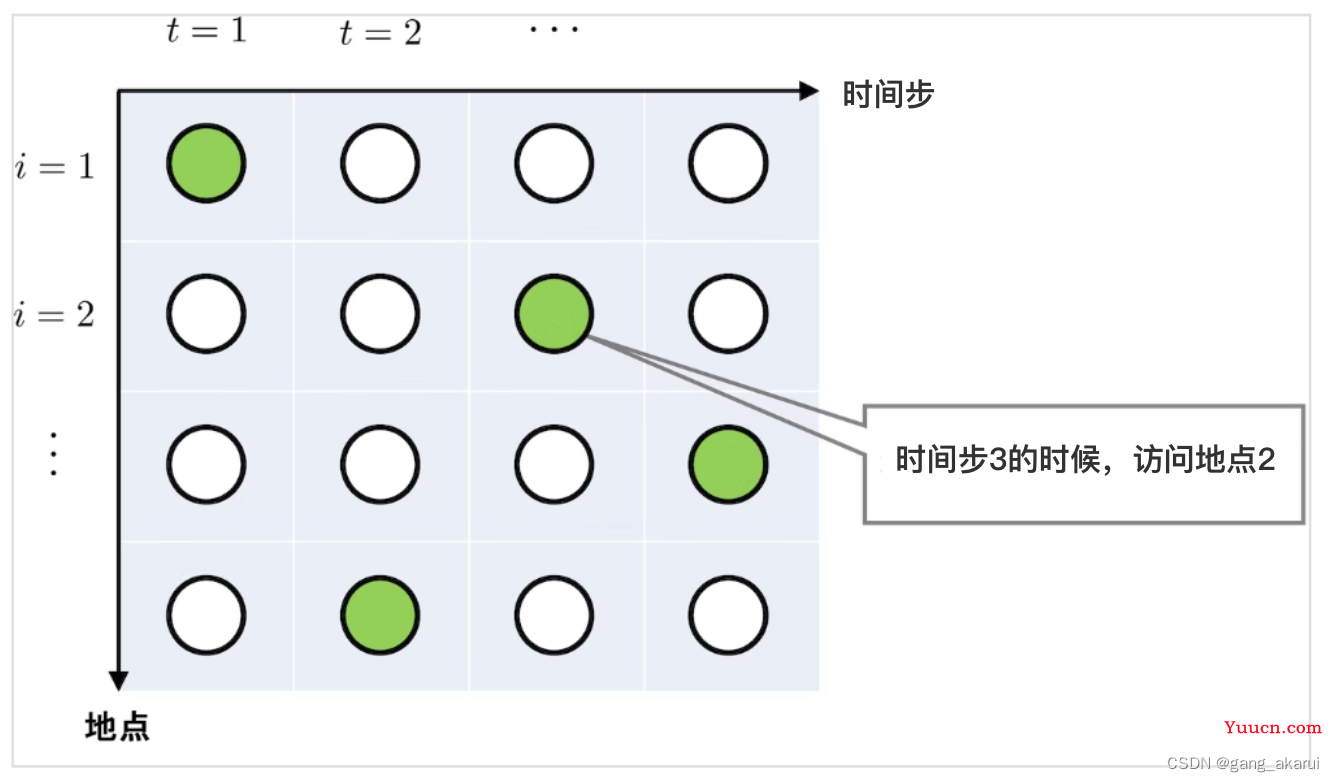
2.约束条件
约束条件比较简单,先从约束条件解释,这里有2个约束可以解释如下:
- 每个时间步只能访问一个地点。
=> 上图矩阵里的每列元素之和必须为1。也就是每列中只有一个元素为1。 - 每个地点都访问过一次。
=> 上图矩阵里的每行元素之和必须为1。也就是每行中只有一个元素为1。
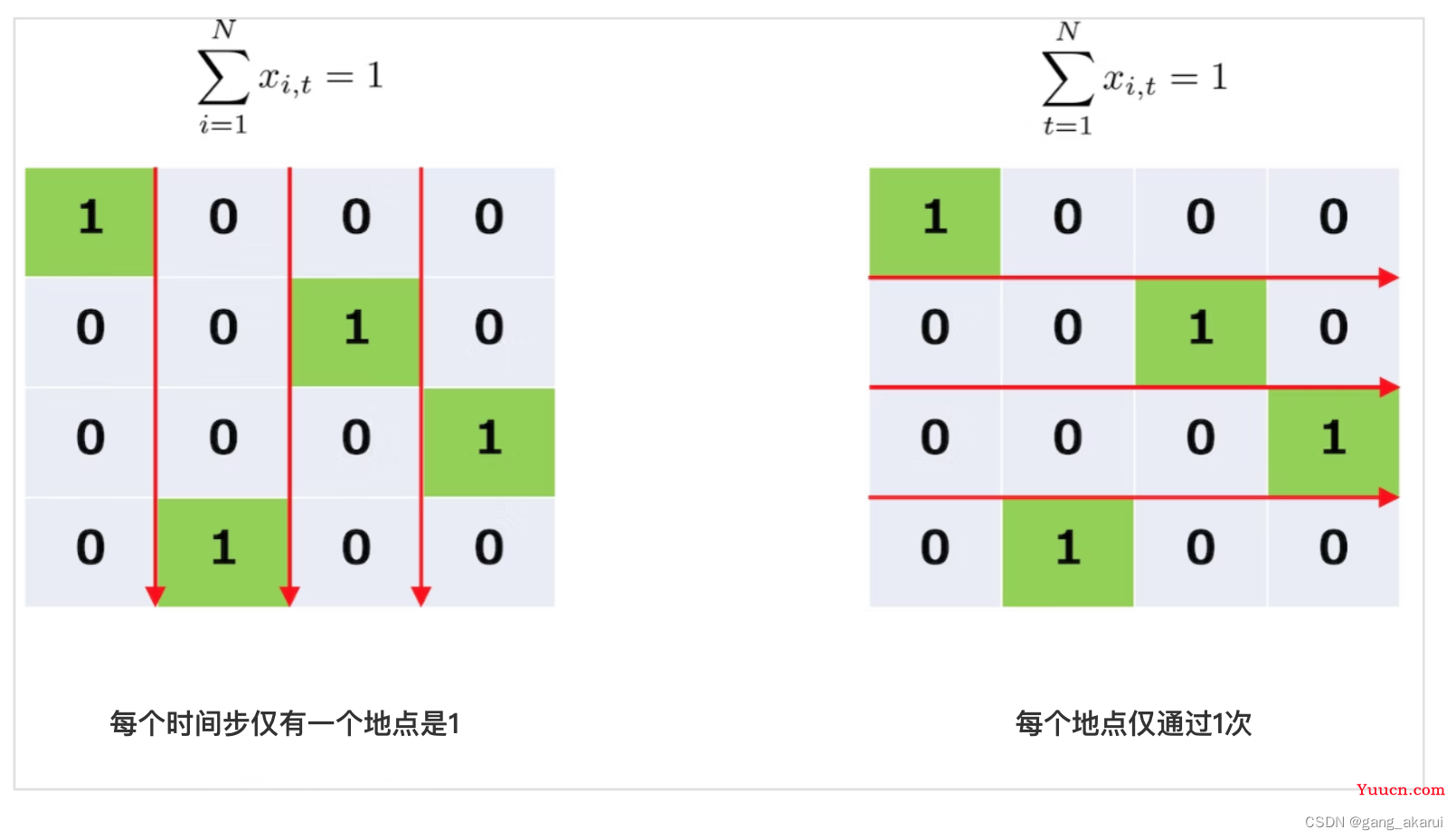
具体表达式如下:
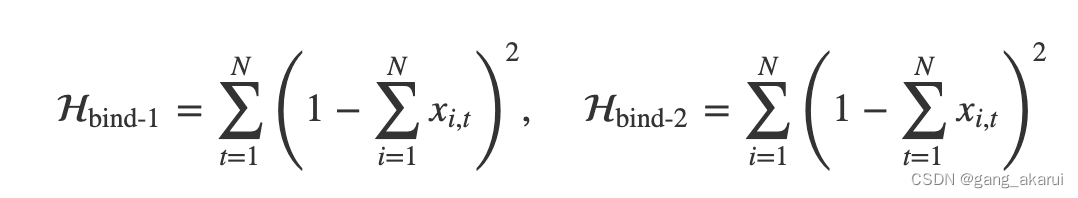
3.目标函数
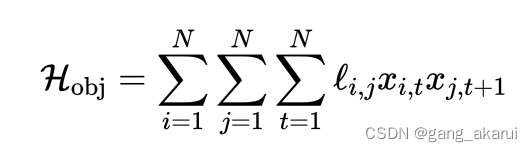
解析:
-
x
i
,
t
x
j
,
t
+
1
x_{i,t}x_{j,t+1}
xi,txj,t+1:
这里的目标函数,最难理解的是
x
i
,
t
x
j
,
t
+
1
x_{i,t}x_{j,t+1}
xi,txj,t+1。可以理解为【
t
t
t时间步访问地点
i
i
i,
t
+
1
t+1
t+1时间步访问地点
j
j
j时,
x
i
,
t
x
j
,
t
+
1
x_{i,t}x_{j,t+1}
xi,txj,t+1=1;其他的情况,
x
i
,
t
x
j
,
t
+
1
x_{i,t}x_{j,t+1}
xi,txj,t+1=0】。 -
∑
i
=
1
N
∑
j
=
1
N
∑
t
=
1
N
\sum_{i=1}^N \sum_{j=1}^N \sum_{t=1}^N
∑i=1N∑j=1N∑t=1N:
该表达式代表了,【
t
t
t时间步访问地点
i
i
i,
t
+
1
t+1
t+1时间步访问地点
j
j
j时,地点
i
i
i和
j
j
j之间的距离
ℓ
i
,
j
\ell_{i, j}
ℓi,j之和】。所以,这个目标函数就代表了,从初始地点,经过所有地点后,回到初始地点的距离总和。
总结
旅行商问题,是比较有实际意义的应用问题,大家能体会到怎么把现实问题抽象出binary变量,然后怎么把制约条件表达出来。因为,上面的建模有两种编程实现方式,为了控制篇幅,下一篇献上Python代码。
在阅读参考文献时,经常会发现资料里的一些小错误,大家以后阅读资料时也要小心啊。
- 参考文献:
[*1] : https://www.nttdata.com/jp/ja/-/media/nttdatajapan/files/news/services_info/2021/012800/012800-01.pdf
[*2] : https://qiita.com/yufuji25/items/0425567b800443a679f7