目录
BP神经网络(Back propagation)反向传播神经网络,也被叫做多层感知机。
输入字段节点个数如何确定
BP神经网络的特点:
隐藏层个数如何确定
BP神经网络如何传递信息
BP神经网络如何修正权重值及常数值
梯度下降法:
我的主页:晴天qt01的博客_CSDN博客-数据分析师领域博主
目前进度:第四部分【机器学习算法】
BP神经网络(Back propagation)反向传播神经网络,也被叫做多层感知机。
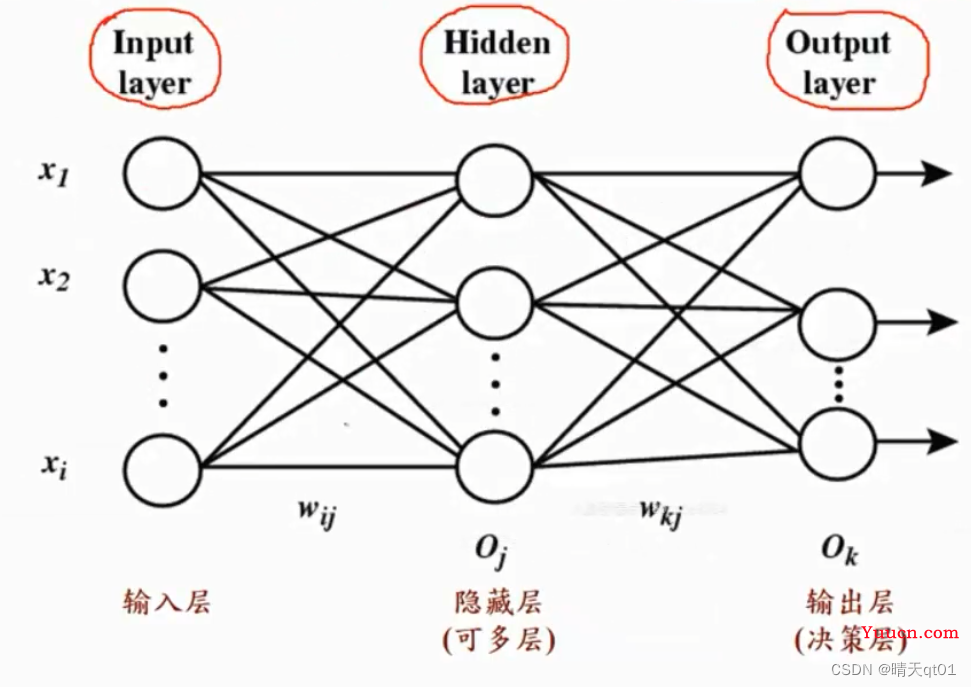
每个圆圈是神经元,每条线被叫做神经键。
隐藏层的神经元越多,处理能力越强,隐藏层也可以多层。
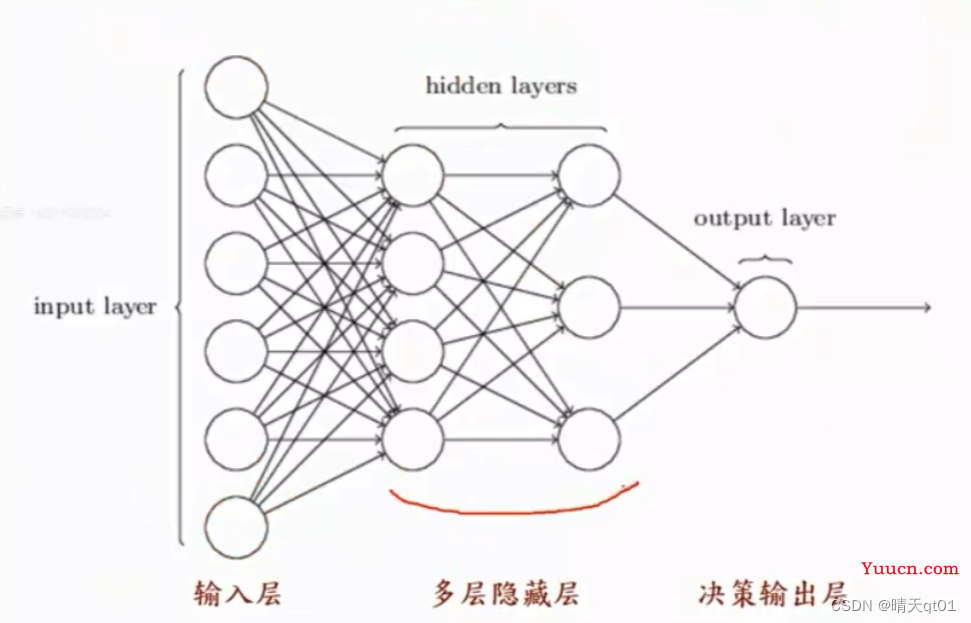
之后深度学习会具体说明层数多好还是层数少单层个数多好。深度学习中深度的意思其实就是隐藏层多层的意思,比如现在有10个神经元,把它们都集中挤在同一层总,那么它的效果经过研究表明,其实没有2层5个神经元的效果好的。
但是很少能做到很多层因为,隐藏层越多,要求你的参数(字段,特征)量越多,数据量也要越多。否则就会出现过拟合情况。
所以我们一般用一层或两层。不要隐藏层,也是可以。案例如下图,这种情况一般做的是二元分类问题,或者是回归预测问题。它就可以没有隐藏层。没有隐藏层的神经网络,其实就是一个比较简单只能处理二分类的问题。
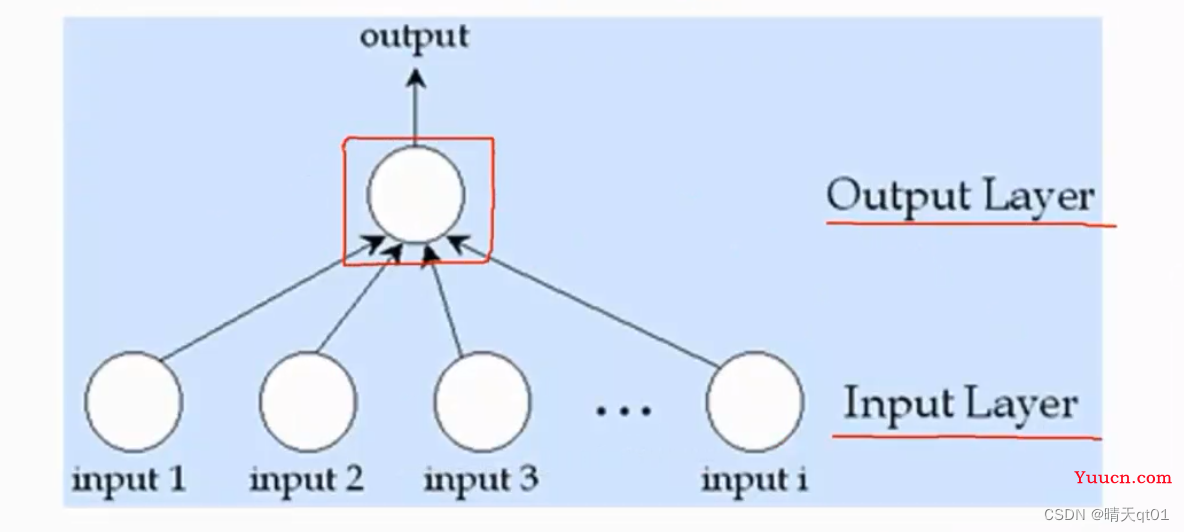
如果我们添加了隐藏层,那么我们就可以处理比较复杂的二分类问题。
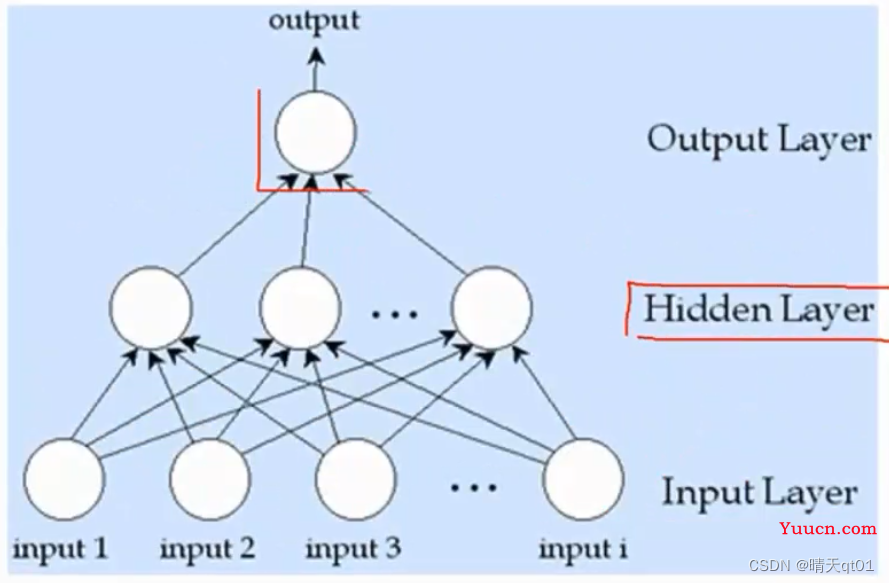
如果我们的输出层有多个节点(神经元),那么我们就可以处理多分类的问题了
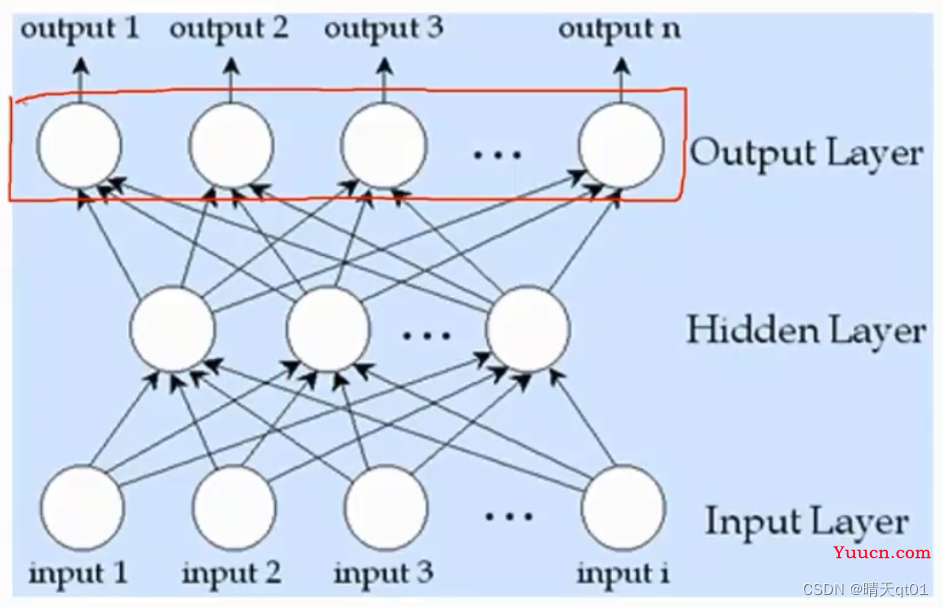
根据不同的方式去架构BP神经网络,那么就可以解决不同的问题。下面我们来举几个案例。
输入字段节点个数如何确定
案例1:杂志喜好预测范例:
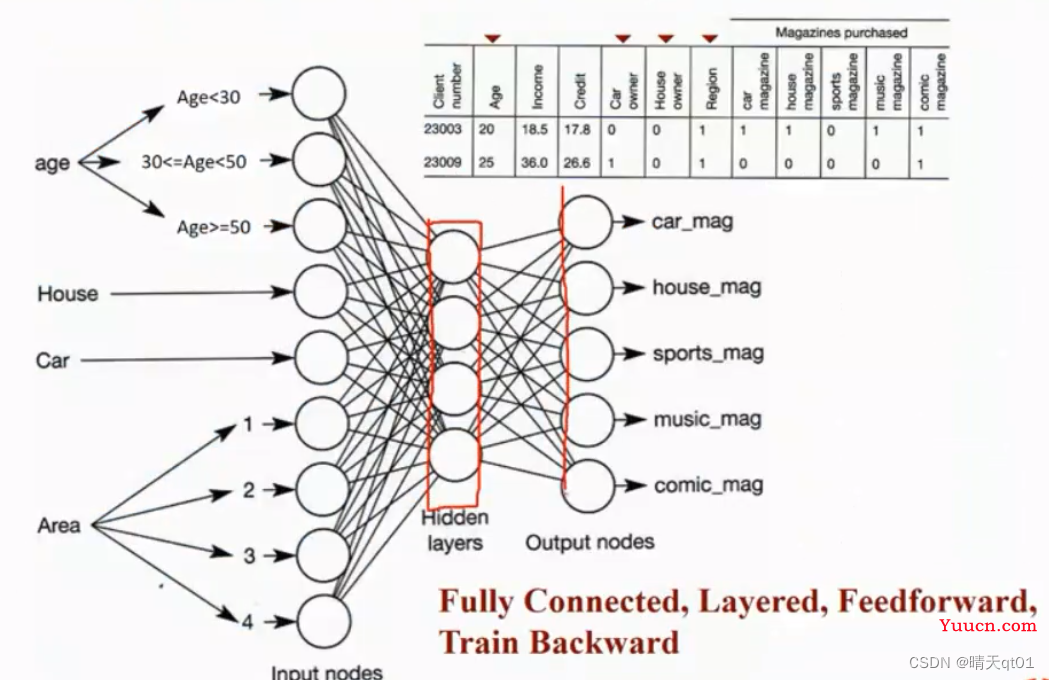
我们可以发现它有5个节点,那么它做的就是分5类的问题。因为这个杂志社希望得到人们5个杂志的喜好。所以输出节点就设置了5个。
我们之前说多分类问题要使用softmax,但是这题就不用softmax,因为人们对杂志的偏好,不一定是只能偏好一类,而是可以同时喜欢多种杂志。而softmax会导致最后的结果累积求和为1,总和不一定要为1。这里我们就直接使用sigmoid function其实就可以了。
我们使用某个功能一定要了解它背后的底层原理,再去使用。
这里一共输入层4个字段,因为神经网络只能接受数值型的输入,使用我们要对分类变量进行编码。
年龄要进行离散化。这里处理方法一般是摊平处理,也就是one hot encoding编码模式,也就是在3个神经元里小于30岁对应1,0,0,大于30小于50对应0,1,0,最后一个范围对应0,0,1。只有一个神经元里有数值1.
因为我们输出结果是0-1之间,所以我们也会希望输入字段是0—1之间。也就是要进行数据预处理。尽量保证输入字段0-1
AREA也是一样,如果句子在area2那就输入0100.
我们就是要根据字段(特征)是数值型还是分类型,安排输入字段。
BP神经网络的特点:
Fully connected:全连接
Layered:3个层次
Feedforword:数据是由左往右处理,从输入层到隐藏层到输出层。
Train Backward:训练权重值时,从后往前进行权重优化。等会有案例
案例2:

第一行是我们要进行辨识的数字,第二行是我们对图片预处理,进行分割,然后进行数值识别。
我们假设数值照片长宽是固定值28*28.因为我们输入字段的神经元是固定的。所以进来的图片也得是固定大小。
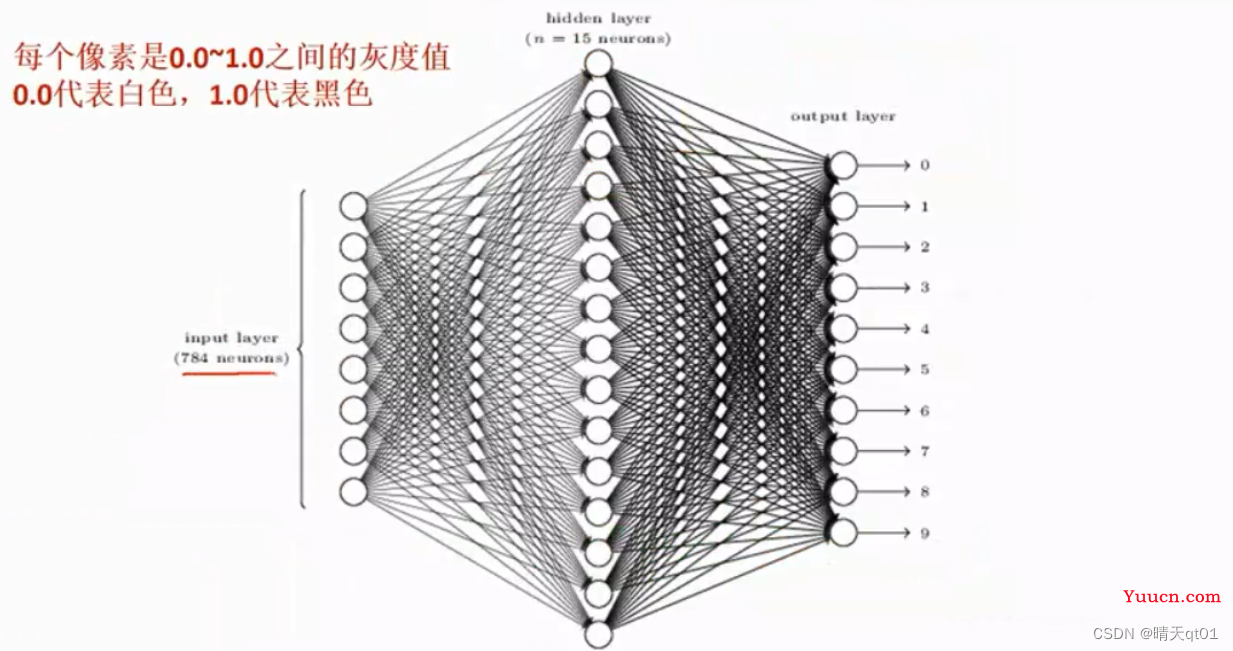
输出层个数就是像素的个数。28*28=784,这里输入字段是每个像素的灰度值。我们颜色有灰度:一般是0~255,黑色就是0,白色就是255.那么我们对输入字段进行处理,因为我们普遍希望认为0是白色。,1-灰度除以255得到0~1的灰度值,此时0就代表白色,1代表黑色。不用1减的话0就是黑色,1就是白色
隐藏层用了15个节点。
输出层我们需要它辨识出0~9其中一个数字。这时我们就需要它的概率值累计求和为1,也就是其中只能有一个数字被选中。这时就不能用函数sigmoid function,而是采用softmax function
隐藏层个数如何确定
隐藏层的使用个数是需要揣摩的超参数。如果隐藏层越多,说明机器能力越强,但是也容易出现过拟合的情况,如果隐藏层太少,机器有会出现智能不足的情况。所以隐藏层要使用多少个,需要认真揣摩。如果数量过多的过拟合情况就相当于,他只是把这些情况记忆下来,得到结果。就不像我们需要的机器学习了,他的泛化效果(测试效果)就会差
再同等准确率的情况下,这边建议选择隐藏层较少的模型。
我们一般有一个公式输入层的节点个数乘以输出层节点个数开根号。然后对这个数字向下取。同等准确率,层数越少越好。
比如案例1的杂志喜好预测,输出层有9,输出层有5,数值大概6.几。那么我们就采用以6开始向下调整。我们查看654的能力,发现准确率差不多。那么我会采用4的结果,如果采用的是3的发现能力比4要差不少,那就说明,智能不足,于是最终确定下来为4.这个要一个一个尝试。
案例2,748*10开更好,我们采用的却是15,就是因为它泛化能力最强。
总结:建立BP网络步骤如下
1.建立网络架构:
输入层的表示方法(数值型,类别型,尽量0-1)
选择隐藏层数,和个数。要考虑到泛化能力问题
2.选择训练数据
得到一组的最佳的权重值,让我们得到的输出向量与目标向量的误差最小包含界限值西塔,或者叫偏置项
3.训练结果:解读训练结果和预测结果。
BP神经网络如何传递信息
先对数据进行训练。得到feedforward的结果
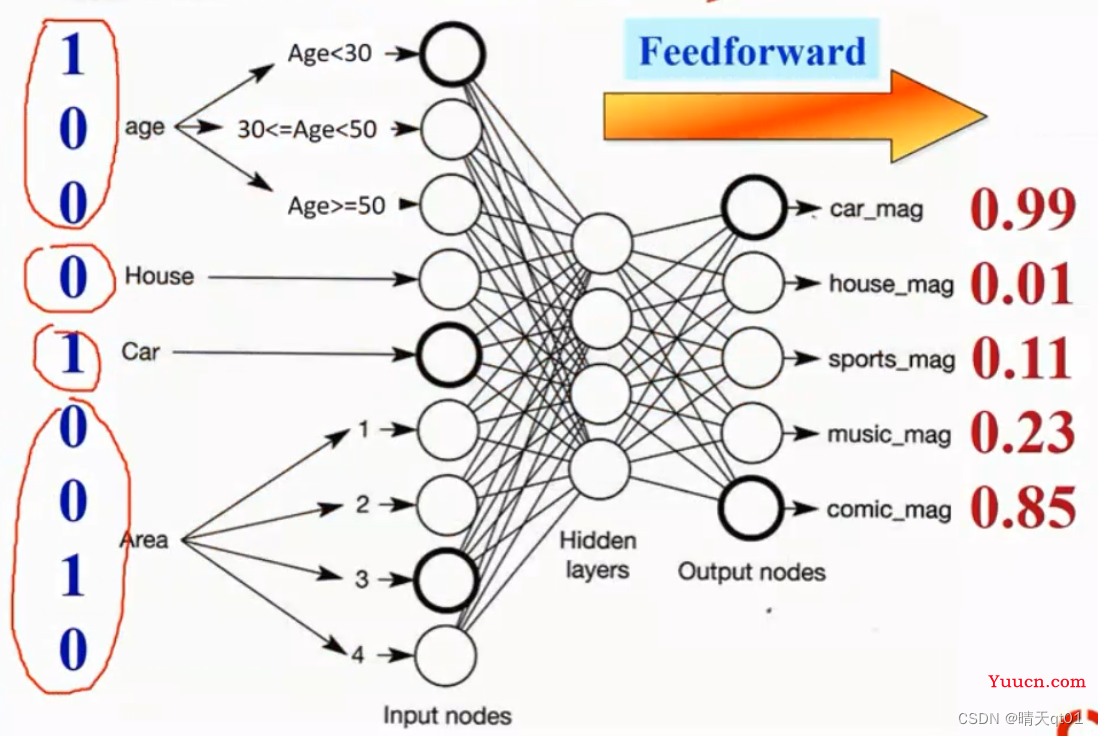
所以我们就说它对汽车和漫画杂志感兴趣。
那如果我们希望得到最佳的权重值,我们就得先了解神经元的构造。也就是最基础的感知机的构造,里面的内容是什么。因为其实输入层到隐藏层是组合求和的过程,,主要的隐藏层和输出层的内容
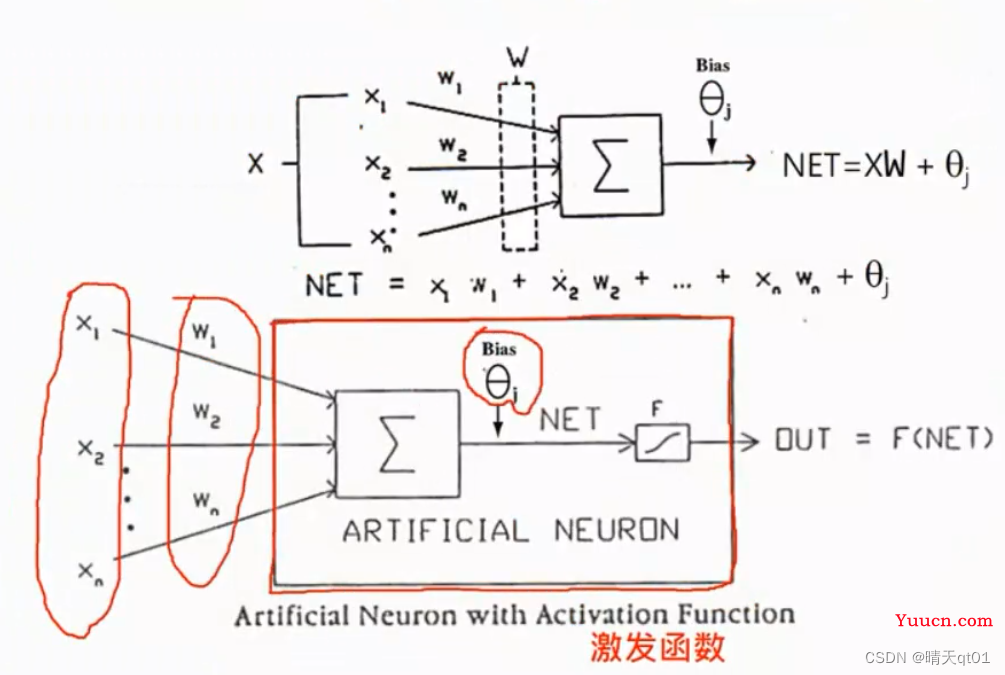
第一步把输入字段放进去的过程是组合函数,然后用激活函数输出。
就是神经元的数值乘以它的权重,然后加上bias的值,然后通过激活函数(activation function)得到函数
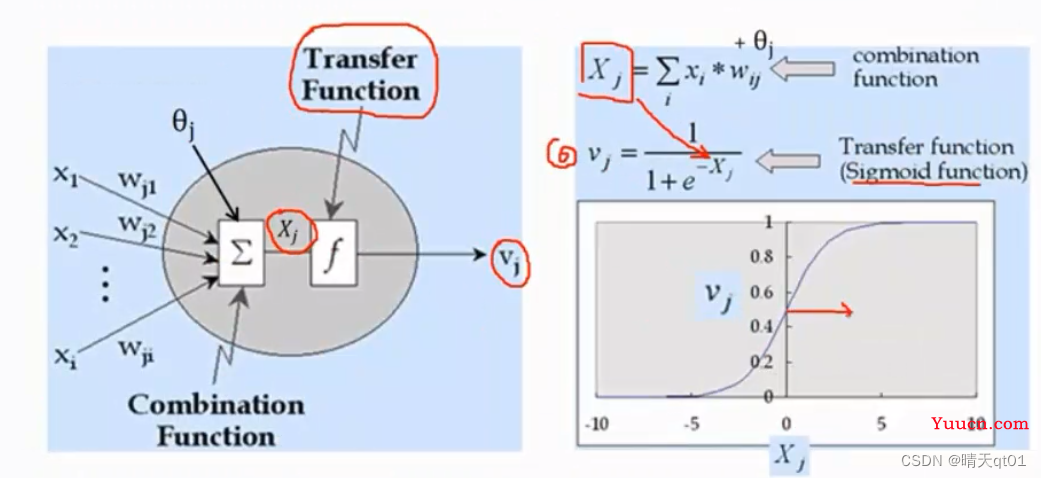
其中的activation function激活函数也可以被叫做TransferFinction转变函数。
这里的激活函数就是sigmoid function
BP神经网络手算案例:
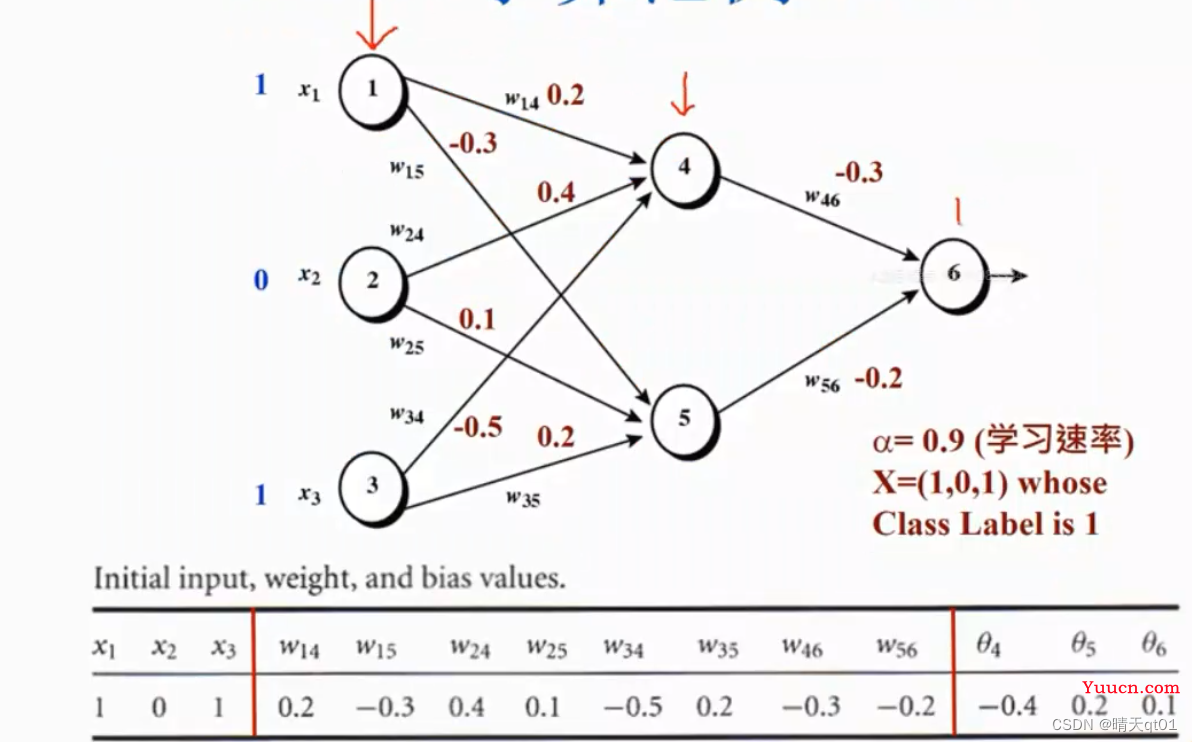
这是一个bp神经网络,里面有3个层次,输入层3个,输出层1个,隐藏层2个。而且是全线连接。
权重值刚开始是根据一笔输入记录随机产生。然后3个层次完全连接
偏置值Bias也就是里面的西塔 也是随机产生:在-1到1之间随机产生
然后我们输入记录输入进去
神经元1:1 神经元2:0 神经元3:1
然后这个1会传输下去到2个隐藏层节点,同理0和1也是一样。到这里输入层就完全结束。隐藏层,前半段开始。
手算介绍:
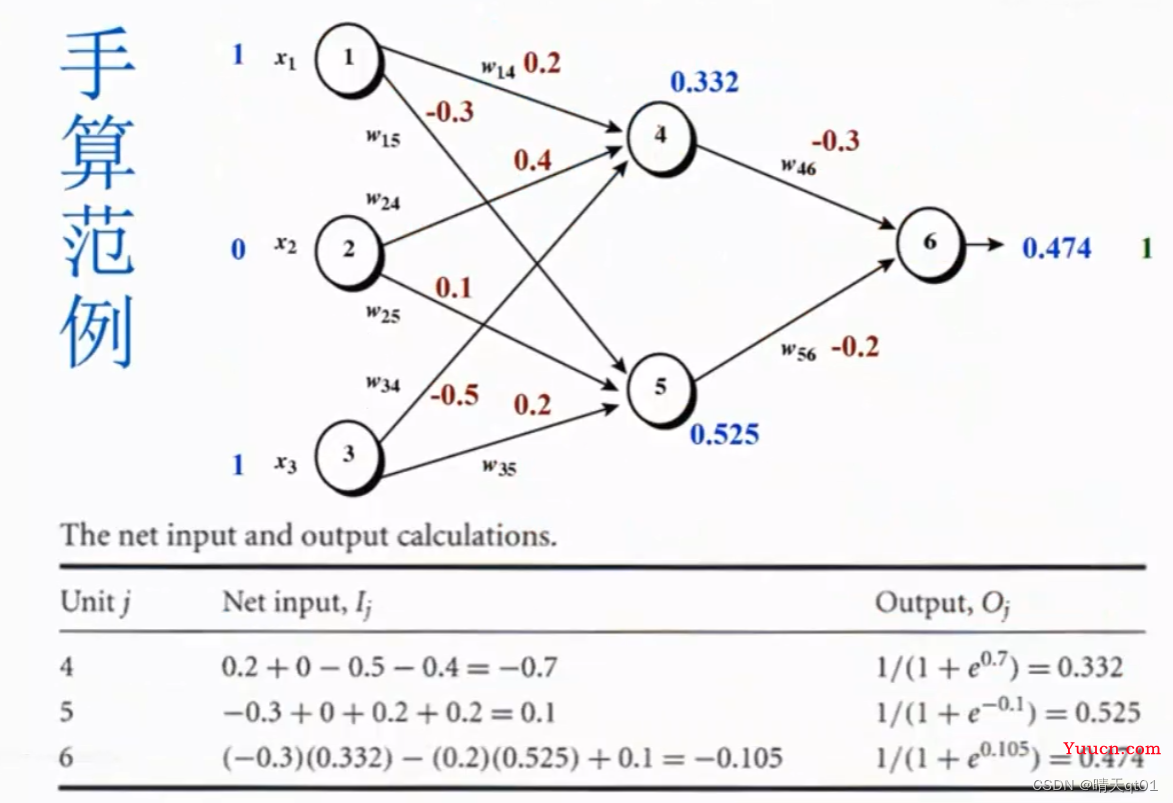
我们随机出权重,然后按路线计算隐藏层数值和输出结果,如上表。,
比如4号节点,就可以通过上表的组合函数计算3个神经元的数值得到0.332,以此类推
得到0.474的结果,但是我们的目标实际结果是1,使用权重值和bias所以不是很理想,为什么不是很理想呢?因为我们都随机产生的权重和bias的值,这也是我们能预期到的结果。现在我们就要进行backward training。
BP神经网络如何修正权重值及常数值
逆向权重和偏执项的修正(backward training):
那么我们现在就bakeward training逆向权重和偏执项的修正。
它会去修复隐藏层到输出层的组合函数,和激活函数。
这个修正好之后,然后再去修正输入层与隐藏层的内容。
我们在逐步从右向左修正误差的过程中,后面的误差是会影响到前面的误差。把误差由后往前传递反向传递。
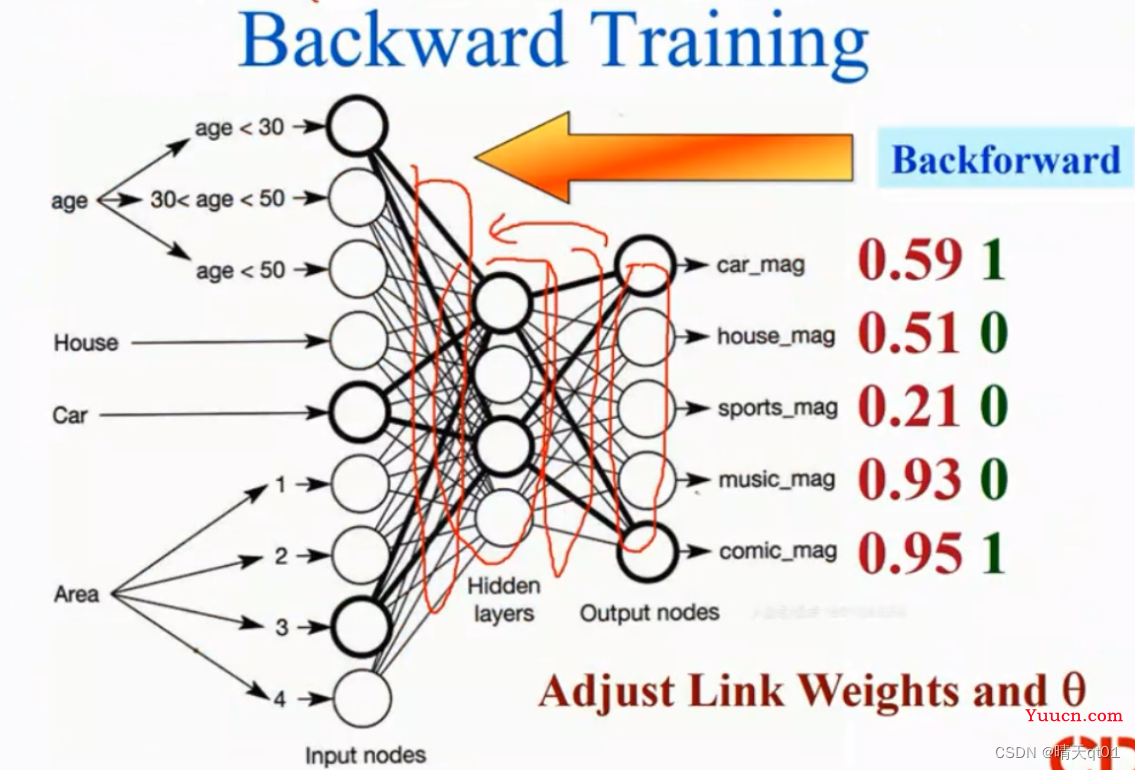
比如这个杂志,我们将数据放进去,发现预测结果误差很大,我们需要的结果是1,0, 0, 0 ,1,预测结果是0.59 ,0.51 ,0.21 ,0.93 ,.095
这个时候就需要backward training
误差如何计算呢。把每个值与目标值的差平方,累加求和。就比如上图就应该是(1-0.59)2+(0-0.51)2……=误差
下图就是error function
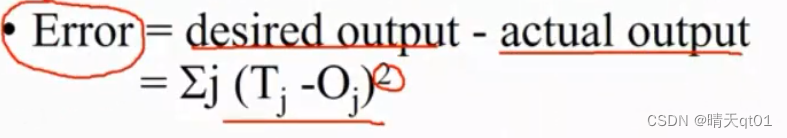
也就是我们先feedforword从左往右生成权重和bias的值,然后比较输出层和标准结果再求出误差值,误差值作为我们的评分依据,我们要将它降为最低。
我们要将这个误差进行一个偏微分,就会出现极值,我们利用公式,使误差方程式得到极小值(只能是极小值,不能是最小值),就可以进行修正。微分过程我们就不细讲了,比较繁琐。需要材料的可以私聊我。
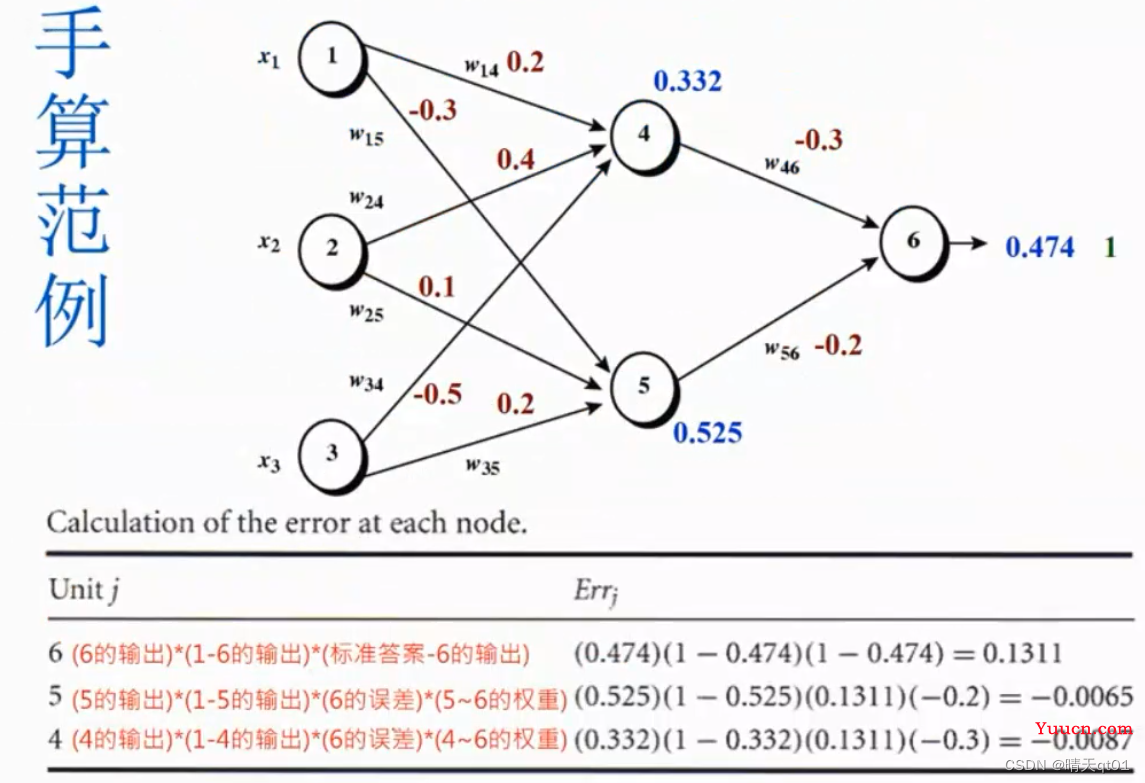
这边直接给出微分结果。这些是偏微分的结果。
比如6号节点的误差,用它的输出值乘以误差值的平方就是,我们这次计算出来的偏离误差多少,。
同一层的修正微分公式都是差不多。
一般同一层的误差公式都是类似的。
这样我们就可以得到我们各节点的节点误差,那么我们就可以利用节点误差来修正权重值误差。
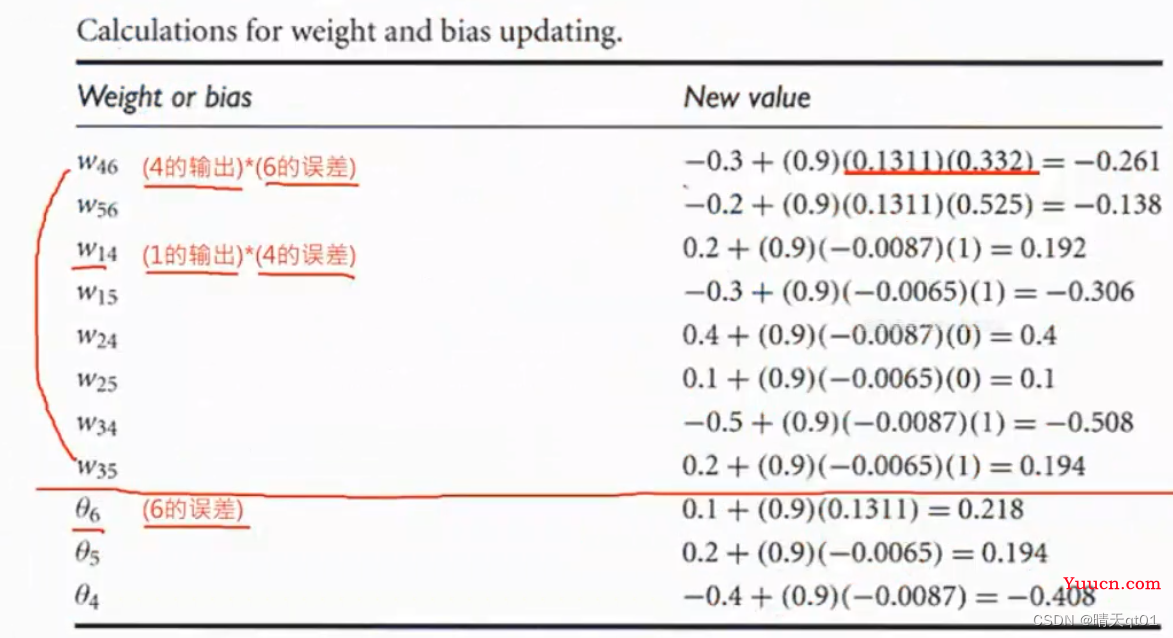
上图就w46就是节点4和节点6的连接键位,它的值通过之前4的误差和6的误差进行计算修正。后面的数值就是该权重应该调整的值。
这里也是微分的结果,之后对数学感兴趣的可以向我要资料。公式前面的0.9代表的就是学习速率,由我们主动设置,后面深度学习会说明如何设置动态的学习速率。
我们这个时候拿我们现在这个修正好的结果去跑回归会发现,其实很难做到一步到位,选择输入字段101的结果不是立马就变为1或者0.99了,更大可能是由0.43变为0.5多。我们要一直进行跑逆向权重和bias的修正就可以收敛到比较好的结果。这个修正不是一步到位的,可能进行500次,结果可能输出的就变成0.93,所以去跑神经网络是很耗费时间的。
为什么要进行多次跑修正呢,这个是为了这种情况不发生,比如我现在的权重值是0.3,最佳值是0.25,但是你学习效率设置很大。那么修改之后系统认为需要前进0.1,权重就变成了0.2,第二次修改又会变为0.3.来回反复,永远达不到最优。
学习速率Leaning rate的设置就起到了很大的作用。如果学习效率设置的高,可能逼近的速度快,但是不能得到比较好的最佳值,如果比较少,可能会得到比较好的最佳值,但是它会花更多的时间。
传统的神经网络都是我们主动设置leaning rate 。
但是在深度学习里面,就会使用动态的leaning rate 刚开始大,后面可能就小了。传统的BP神经网络都需要主动去设置学习速率。目前的深度学习就可以做到动态调整学习速率。刚开始学习速率高,后面学习速率低。
梯度下降法:
为什么我们不能一步到位,而是不断调整呢,因为我们使用的这个方法是梯度下降法:因为我们的逆向权重和偏执项的修正是通过一次微分求斜率,斜率的正负决定了权重要增加还是降低,但是不能得到,但是有时候实际的误差函数不是怎么漂亮的,它是有两个谷底的,例如下图右,我们第一次得到的权重值,如果权重误差在左,就只能下降到左边的低谷,而在右边,就能下降到右边的低谷,所以我们就把BP神经网络求出的最佳值,叫做区域最佳值。
后面我们可能进行一些方法的调整,容易得到全域最佳解,不过一般都是区域最优解。