0 前言

在曝光融合（Exposure Fusion）算法问世之前，多曝光序列合成用于显示的HDR需要两个步骤，第一步是将多张不同曝光的低动态范围图像合成为HDR（例如Debevec提出的加权融合方法），通常HDR为12bit或者16bit；第二步是通过tonemapping对高动态范围HDR进行压缩以支持低动态范围显示设备（例如Durand提出的基于双边滤波的tonemapping算法），一般会压缩至8bit。

曝光融合算法的优势在于不需要标定相机响应曲线，并且跳过tonemapping步骤，直接合成用于显示的高动态范围图像。

1 算法细节

1.1 Naive

1.1.1 主要思想

对于多曝光图像序列，取每一张图像中最有价值的部分用于合成。例如，曝光时间长的图像中暗区细节丰富同时噪声水平低，那么暗区就是有价值的部分。显然，需要一个指标来衡量每张图像中哪些像素有价值，然后通过计算每张图每个像素的价值指标当作对应的权重，最终通过加权融合的方式得到HDR。

1.1.2 权重计算

从对比度、饱和度和亮度三个维度对像素的价值进行评估：

对比度
这里的对比度指的是图像的梯度，对于边缘和纹理等重要的信息分配很大的权重。具体地，对图像的灰度图执行拉普拉斯滤波，结果取绝对值作为对比度指标 $C(I_k)$ 。
$C(I_k)=|\triangle_{gray}(I_k)|$
饱和度
RGB三通道之间差异大的可视为饱和度高的区域，反之，对于过曝或者欠曝区域RGB三通道的值趋于一致，饱和度较低。因此，可将RGB三个通道之间的标准差作为饱和度指标。
$S_{k,i,j}=\sqrt{\frac{(I_{k,i,j}^{B}-M_{k,i,j})^2+(I_{k,i,j}^{G}-M_{k,i,j})^2+(I_{k,i,j}^{R}-M_{k,i,j})^2}{3}}$ $M_{k,i,j}=\frac{I_{k,i,j}^{B}+I_{k,i,j}^{G}+I_{k,i,j}^{R}}{3}$
亮度
对于归一化至0~1范围的图像，将取值在0.5左右的像素视为曝光良好，应该分配很大的权重；接近0和1的分别为欠曝和过曝应该分配很小的权重。像素值与其对应权重的关系符合均值为0.5的高斯分布：
$E_{k.i,j}=e^{-\frac{(I_{k,i,j}^{B}-0.5)^2}{2\sigma^2}} \cdot e^{-\frac{(I_{k,i,j}^{G}-0.5)^2}{2\sigma^2}} \cdot e^{-\frac{(I_{k,i,j}^{R}-0.5)^2}{2\sigma^2}}$

获取以上3个指标后，就能计算每个像素对应的权重：
$W_{i,j,k}=(C_{i,j,k})^{w_c}\cdot (S_{i,j,k})^{w_s}\cdot (E_{i,j,k})^{w_e}$ 默认 $w_c=w_s=w_e=1$ ；另外，为了保证多张图像在同一位置的权重和为1，需要在图像数量维度上对权重进行归一化：
$\hat{W}_{{ij,k}}=\frac{{W}_{{ij,k}}}{\sum_{k^{\prime}=1}^{N}{W}_{{ij,k^{\prime}}}}$

1.1.3 融合

根据计算的权重对原始图像进行加权求和，即可得到融合后的图像：
$H_{ij}=\sum_{k=1}^{N}\hat{W}_{{ij,k}}\cdot I_{ij,k}$

这样粗糙融合的结果存在一个问题，在权重尖锐过渡的区域，由于每张图像的曝光时间不同，绝对强度也不同，导致融合后灰度跳变太大，图像中呈现很多黑色和白色斑点，与噪声形态类似。

权重尖锐过渡区会出现问题，那么可以让其平滑一点，提到平滑自然而然就想到了高斯滤波。作者对权重图做高斯滤波后再进行合成，虽然斑点问题得到了缓解，但是在边缘处会出现光晕现象。

既然光晕是由于边缘处的权重被平滑所导致的，可以考虑使用保边滤波代替高斯滤波。

1.2 Multi-resolution

由于naive版本的融合方式不能完全解决黑白斑点的问题，并且会引入光晕这样的新问题。因此，作者提出了使用拉普拉斯金字塔融合的方式，其流程如下图所示：

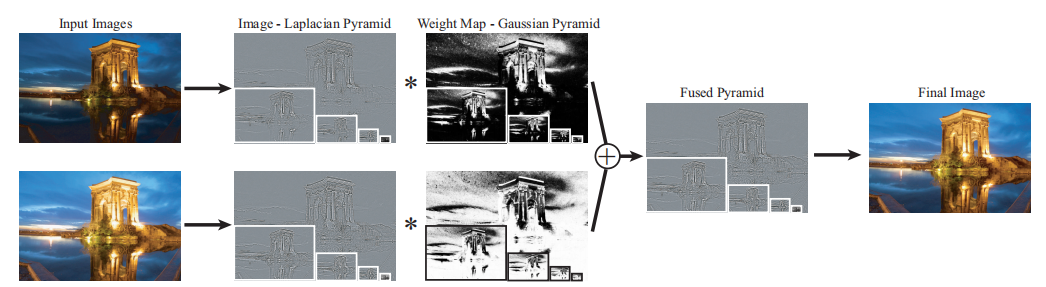
简单来说，就是从不同曝光的原始图像中分解出拉普拉斯金字塔，对应的权重图中分解出高斯金字塔，然后分别在每个尺度下进行融合，得到融合后的拉普拉斯金字塔。最后，从拉普拉斯金字塔的顶层开始向上采样，叠加同尺度的拉普拉斯细节，再向上采样和叠加细节，递归至最高分辨率，得到最终的结果。（此处有一个点需要注意，拉普拉斯金字塔的顶层就是原始图像高斯金字塔的顶层）

为什么拉普拉斯金字塔融合效果好？
将平坦区和尖锐过渡区（如边缘）分开融合，平坦区融合使用的是经过多次高斯滤波和下采样后的权重图，仅在比较大的边缘纹理处变化剧烈；由于拉普拉斯金字塔中只保留了边缘等高频信息，因此在拉普拉斯金字塔上对尖锐过渡区进行融合不会影响平坦区。

2 实验

import os
import sys
import glob
import numpy as np
import cv2
import argparse
def show_image(message, src):
    cv2.namedWindow(message, 0)
    cv2.imshow(message, src)
    cv2.waitKey(0)
    cv2.destroyAllWindows()
def gauss_curve(src, mean, sigma):
    dst = np.exp(-(src - mean)**2 / (2 * sigma**2))
    return dst
class ExposureFusion(object):
    def __init__(self, sequence, best_exposedness=0.5, sigma=0.2, eps=1e-12, exponents=(1.0, 1.0, 1.0), layers=7):
        self.sequence = sequence  # [N, H, W, 3], (0..1), float32
        self.img_num = sequence.shape[0]
        self.best_exposedness = best_exposedness
        self.sigma = sigma
        self.eps = eps
        self.exponents = exponents
        self.layers = layers
    @staticmethod
    def cal_contrast(src):
        gray = cv2.cvtColor(src, cv2.COLOR_BGR2GRAY)
        laplace_kernel = np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]], dtype=np.float32)
        contrast = cv2.filter2D(gray, -1, laplace_kernel, borderType=cv2.BORDER_REPLICATE)
        return np.abs(contrast)
    @staticmethod
    def cal_saturation(src):
        mean = np.mean(src, axis=-1)
        channels = [(src[:, :, c] - mean)**2 for c in range(3)]
        saturation = np.sqrt(np.mean(channels, axis=0))
        return saturation
    @staticmethod
    def cal_exposedness(src, best_exposedness, sigma):
        exposedness = [gauss_curve(src[:, :, c], best_exposedness, sigma) for c in range(3)]
        exposedness = np.prod(exposedness, axis=0)
        return exposedness
    def cal_weight_map(self):
        weights = []
        for idx in range(self.sequence.shape[0]):
            contrast = self.cal_contrast(self.sequence[idx])
            saturation = self.cal_saturation(self.sequence[idx])
            exposedness = self.cal_exposedness(self.sequence[idx], self.best_exposedness, self.sigma)
            weight = np.power(contrast, self.exponents[0]) * np.power(saturation, self.exponents[1]) * np.power(exposedness, self.exponents[2])
            # Gauss Blur
            # weight = cv2.GaussianBlur(weight, (21, 21), 2.1)
            weights.append(weight)
        weights = np.stack(weights, 0) + self.eps
        # normalize
        weights = weights / np.expand_dims(np.sum(weights, axis=0), axis=0)
        return weights
    def naive_fusion(self):
        weights = self.cal_weight_map()  # [N, H, W]
        weights = np.stack([weights, weights, weights], axis=-1)  # [N, H, W, 3]
        naive_fusion = np.sum(weights * self.sequence * 255, axis=0)
        naive_fusion = np.clip(naive_fusion, 0, 255).astype(np.uint8)
        return naive_fusion
    def build_gaussian_pyramid(self, high_res):
        gaussian_pyramid = [high_res]
        for idx in range(1, self.layers):
            gaussian_pyramid.append(cv2.GaussianBlur(gaussian_pyramid[-1], (5, 5), 0.83)[::2, ::2])
        return gaussian_pyramid
    def build_laplace_pyramid(self, gaussian_pyramid):
        laplace_pyramid = [gaussian_pyramid[-1]]
        for idx in range(1, self.layers):
            size = (gaussian_pyramid[self.layers - idx - 1].shape[1], gaussian_pyramid[self.layers - idx - 1].shape[0])
            upsampled = cv2.resize(gaussian_pyramid[self.layers - idx], size, interpolation=cv2.INTER_LINEAR)
            laplace_pyramid.append(gaussian_pyramid[self.layers - idx - 1] - upsampled)
        laplace_pyramid.reverse()
        return laplace_pyramid
    def multi_resolution_fusion(self):
        weights = self.cal_weight_map()  # [N, H, W]
        weights = np.stack([weights, weights, weights], axis=-1)  # [N, H, W, 3]
        image_gaussian_pyramid = [self.build_gaussian_pyramid(self.sequence[i] * 255) for i in range(self.img_num)]
        image_laplace_pyramid = [self.build_laplace_pyramid(image_gaussian_pyramid[i]) for i in range(self.img_num)]
        weights_gaussian_pyramid = [self.build_gaussian_pyramid(weights[i]) for i in range(self.img_num)]
        fused_laplace_pyramid = [np.sum([image_laplace_pyramid[n][l] *
                                         weights_gaussian_pyramid[n][l] for n in range(self.img_num)], axis=0) for l in range(self.layers)]
        result = fused_laplace_pyramid[-1]
        for k in range(1, self.layers):
            size = (fused_laplace_pyramid[self.layers - k - 1].shape[1], fused_laplace_pyramid[self.layers - k - 1].shape[0])
            upsampled = cv2.resize(result, size, interpolation=cv2.INTER_LINEAR)
            result = upsampled + fused_laplace_pyramid[self.layers - k - 1]
        result = np.clip(result, 0, 255).astype(np.uint8)
        return result
if __name__ == '__main__':
    root_path = sys.argv[1]
    sequence_path = [os.path.join(root_path, fname) for fname in os.listdir(root_path)]
    sequence = np.stack([cv2.imread(path) for path in sequence_path], axis=0)
    mef = ExposureFusion(sequence.astype(np.float32) / 255.0)
    naive_fusion_result = mef.naive_fusion()
    multi_res_fusion = mef.multi_resolution_fusion()
    show_image('muti-resolution', multi_res_fusion)

3 参考

Mertens T, Kautz J, Van Reeth F. Exposure fusion[C]//15th Pacific Conference on Computer Graphics and Applications (PG’07). IEEE, 2007: 382-390.
https://zhuanlan.zhihu.com/p/455674916

标签 Fusion, OS, Sur

【HDR】曝光融合（Exposure Fusion）

文章目录