问题背景
基于伪标记和一致性正则化的各种方法在半监督学习中取得了巨大的成功。然而,作者认为现有的方法可能无法更有效地利用未标记数据,因为它们要么使用预定义/固定阈值,要么使用临时阈值调整方案,导致性能较差,收敛速度较慢。
FlexMatch 证明了不同的类应该有不同的局部(特定于类的)阈值。虽然局部阈值考虑了不同类的学习困难,但它们仍然从预定义的固定全局阈值映射。
在每个类只有1个标记样本的“two-moon”数据集上,以前的方法获得的决策边界在低密度假设下失败。那么,自然会产生两个问题:1)是否有必要根据模型的学习状态来确定阈值?2)如何自适应调整阈值以获得最佳训练效率?
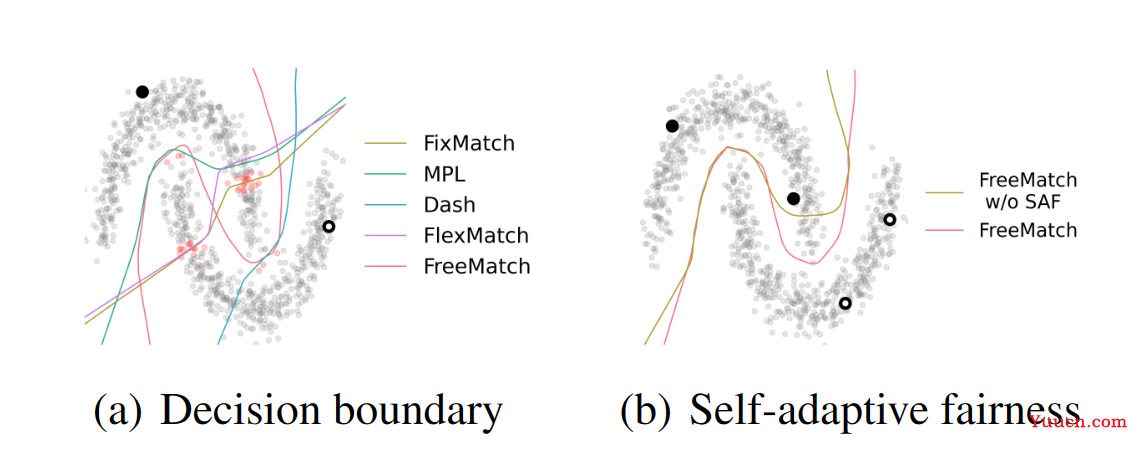
在本文中,作者首先利用一个激励性的例子来证明,不同的数据集和类应该根据模型的学习状态确定它们的全局(特定于数据集)和局部(特定于类)阈值。直观地说,我们需要一个较低的全局阈值来利用更多的未标记数据,并在早期训练阶段加速收敛。随着预测置信度的增加,需要更高的全局阈值来过滤错误的伪标签,以减轻确认偏差。此外,根据模型对其预测的置信度,在每个类上定义一个局部阈值。
作者提出FreeMatch根据每个类的学习状态以自适应方式调整阈值。具体来说,FreeMatch使用自适应阈值(SAT)技术,通过未标记数据置信度的指数移动平均(EMA)来估计全局(特定于数据集)和局部阈值(特定于类)。为了更有效地处理几乎没有监督的设置,进一步提出了一个类公平目标,以鼓励模型在所有类中产生公平(即多样化)的预测。FreeMatch的总体训练目标是最大化模型输入和输出之间的互信息,在未标记的数据上产生自信和多样化的预测。基准测试结果验证了其有效性。
贡献
通过一个激励的例子,讨论了为什么阈值应该反映模型的学习状态,并为设计阈值调整方案提供了一些直观的指导。
提出了一种新的方法FreeMatch,它由自适应阈值(SAT)和自适应类公平正则化(SAF)组成。SAT是一种阈值调整方案,无需手动设置阈值,SAF鼓励多样化的预测。
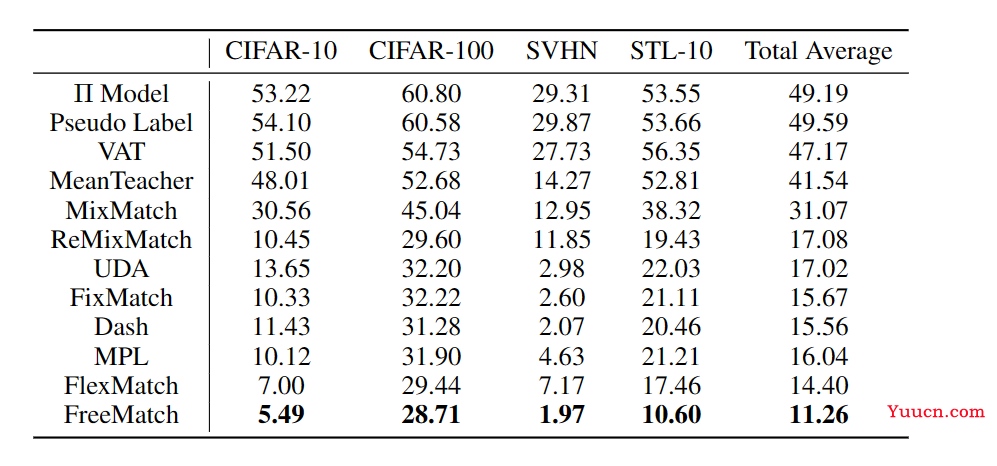
大量的结果证明了FreeMatch在各种SSL基准测试上的优越性能,特别是在标签数量非常有限的情况下(例如,在CIFAR-10上,每个类有一个标记样本的错误减少了5.78%)。
激励例子
将介绍一个二进制分类示例来激励我们的阈值调整方案。尽管简化了实际模型和训练过程,但分析导致了一些有趣的含义,并提供了关于如何设置阈值的见解。
目的是证明自适应性和增加的粒度在SSL的置信阈值的必要性。考虑了一个二元分类问题,其中真实分布是两个高斯的均匀混合(即,标签Y有同样可能是正的(+1)或负的(−1))。输入X具有以下条件分布:
假设μ2 > μ1而不失一般性。假设我们的分类器输出置信度分数:
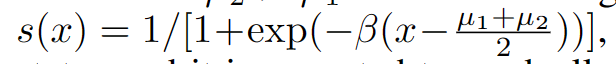
其中β是一个正参数,反映了模型的学习状态,并且随着模型变得更加自信,它在训练过程中会逐渐增长。
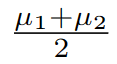
实际上是贝叶斯最优线性决策边界。考虑使用固定阈值τ∈(1/2,1)来生成伪标签的场景。如果s(x) > τ,则为样本x分配伪标签+1;如果s(x) < 1−τ,则为样本x分配伪标签−1。如果1−τ≤s(x)≤τ,则伪标签为0(屏蔽)。
然后推导出下面的定理来说明自适应阈值的必要性:定理2.1。对于上述二元分类问题,伪标签Yp的概率分布如下:
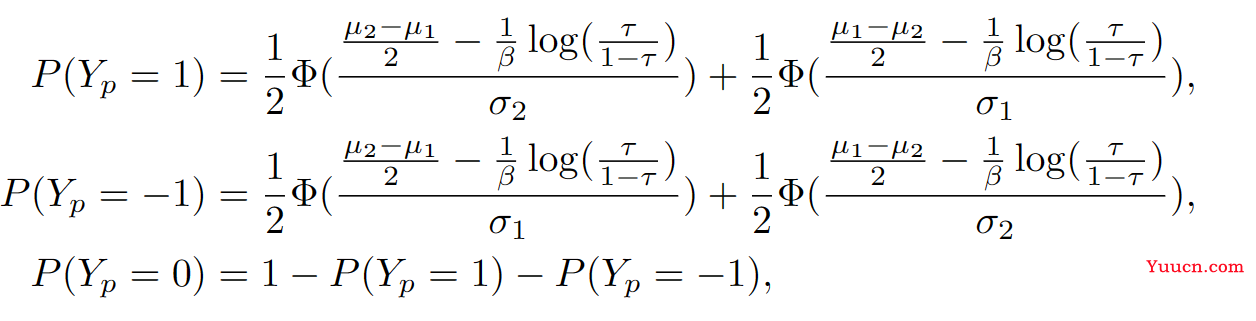
其中Φ为标准正态分布的累积分布函数。随着μ2 - μ1的减小,P (Yp = 0)增大。
定理2.1的含义或解释如下:
简单地说,未标记数据利用率(采样率)1−P (Yp = 0)直接由阈值τ控制。随着置信度阈值τ变大,未标记数据利用率变低。在训练早期,由于β仍然很小,采用高阈值可能导致采样率低,收敛速度慢。
更有趣的是,当σ1 不等于σ2时,P (Yp = 1) 不等于 P (Yp =−1)。事实上,τ越大,伪标签就越不平衡。旨在解决平衡分类问题的意义上来说,这可能是不可取的。不平衡的伪标签会扭曲决策边界,导致所谓的伪标签偏倚。一个简单的补救办法是使用特定于类别的阈值τ2和1−τ1来分配伪标签。
采样率1 -P (Yp = 0)随着μ2 - μ1的减小而减小。换句话说,两个类越相似,未标记的样本越有可能被掩盖。随着两个类别越来越相似,在特征空间中混合的样本越多,模型对其预测的信心就越低,因此需要一个适度的阈值来平衡采样率。否则,我们可能没有足够的样本来训练模型来分类已经很难分类的类。
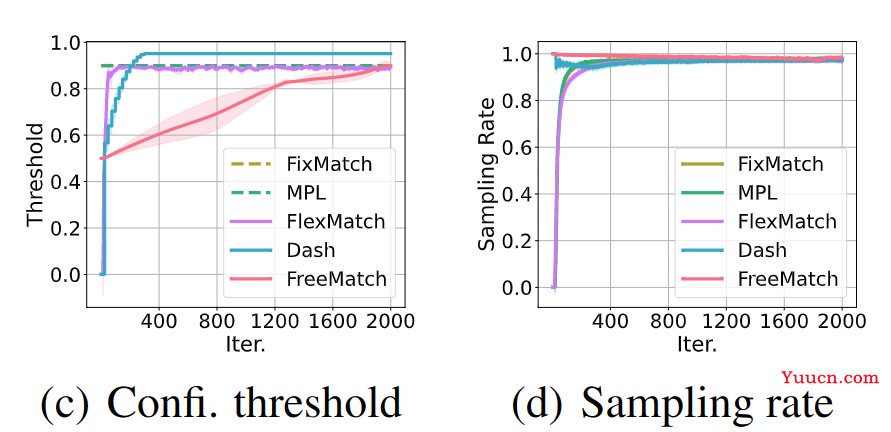
定理2.1提供的直观结果是,在早期训练阶段,τ应该较低,以鼓励不同的伪标签,提高未标记数据的利用率和加快收敛。然而,随着训练的继续和β变大,持续的低阈值将导致不可接受的确认偏差。理想情况下,阈值τ应随β一起增加,以始终保持稳定的采样率。由于不同的类具有不同的类内多样性水平(不同的σ),并且有些类比其他类更难分类(μ2 -μ1较小),因此需要一个细粒度的类特定阈值来鼓励向不同的类公平分配伪标签。挑战是如何设计一个阈值调整方案,考虑到所有的影响,这是本文的主要贡献。通过绘制图1(c)和图1(d)中训练期间的平均阈值趋势和边缘伪标签概率(即采样率)来演示我们的算法。总之,我们应该通过模型的预测来估计学习状态,从而确定全局(特定于数据集的)和局部(特定于类的)阈值。然后,我们详细介绍FreeMatch。
方法FREEMATCH
自适应阈值
作者主张确定SSL阈值的关键是阈值应该反映学习状态。学习效果可以通过校准良好的模型的预测置信度来估计。因此,提出自适应阈值(SAT),通过在训练期间利用模型预测自动定义和自适应调整每个类的置信度阈值。SAT首先估计一个全局阈值作为模型置信度的EMA。然后,SAT通过局部特定类别的阈值调制全局阈值,这些阈值估计为模型中每个类别的概率EMA。当训练开始时,阈值较低,可以接受更多可能正确的样本进入训练。随着模型自信度的增加,阈值自适应增加,过滤掉可能不正确的样本,以减少确认偏差。因此,如图2所示,将SAT定义为τt(c),表示第t次迭代时c类的阈值
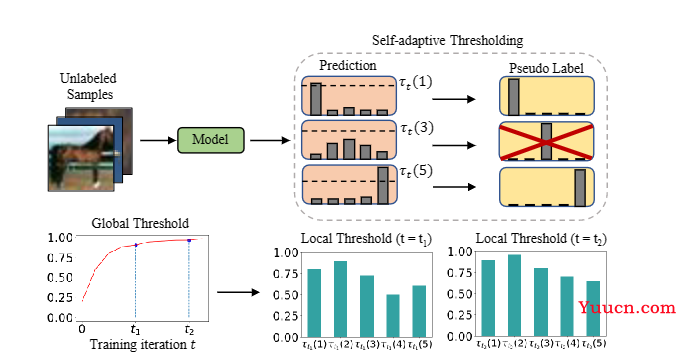
自适应全局阈值 根据以下两个原则设计全局阈值。首先,SAT中的全局阈值应该与模型对无标签数据的置信度有关,反映整体学习状况。此外,在训练过程中,全局阈值应稳定增加,以确保不正确的伪标签被丢弃。将全局阈值τt设为来自未标记数据的模型的平均置信度,其中t表示第t个时间步长(迭代)。然而,由于未标记数据量大,在每一个时间步甚至每个训练周期计算所有未标记数据的置信度都很耗时。相反,我们将全局置信度估计为每个训练时间步置信度的指数移动平均(EMA)。我们将τt初始化为1C,其中C表示类的数量。全局阈值τt定义并调整为:
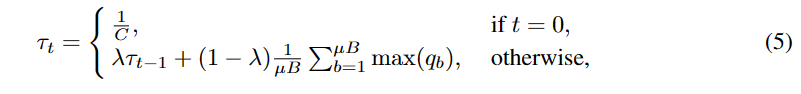
其中λ∈(0,1)是EMA的动量衰减。
自适应局部阈值 局部阈值旨在以特定于类的方式调整全局阈值,以考虑类内的多样性和可能的类邻接性。我们计算模型对每个类c的预测的期望,以估计特定于类的学习状态:
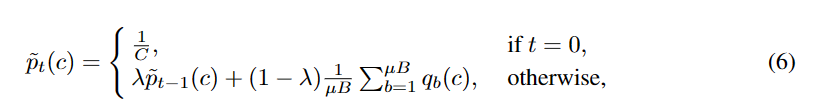
是包含all′pt(c)的列表。综合全局阈值和局部阈值,得到最终自适应阈值τt(c)为:
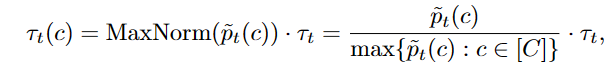
其中MaxNorm是最大归一化
最后,第t次迭代的无监督训练目标Lu为:
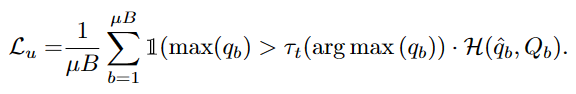
自适应公平
将提到的类公平目标纳入FreeMatch,以鼓励模型对每个类做出不同的预测,从而产生有意义的自适应阈值,特别是在标记数据很少的设置下。与(Arazo等人,2020)中使用统一先验不同,我们使用公式6中模型预测的EMA = pt作为未标记数据上预测分布期望的估计。我们优化了在小批量上p = EμB [pm(y|Ω(ub))]的交叉熵,作为H(Eu [pm(y|u)]的估计。考虑到由于潜在的伪标签分布可能不均匀,提出以自适应的方式调节公平性目标,即通过伪标签的直方图分布对概率的期望进行归一化,以抵消不平衡的负面影响,如:
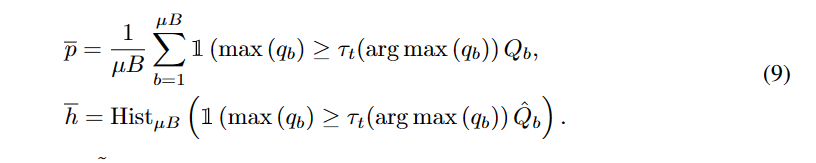
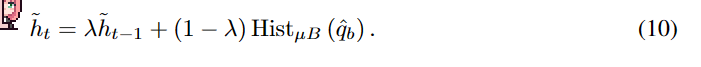
第t次迭代的自适应公平性(SAF) Lf公式为:
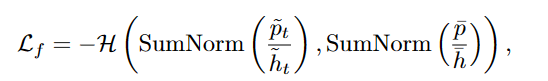
式中SumNorm =(·)/∑(·)。通过直方图分布归一化后,SAF鼓励每个小批的输出概率的期望接近模型的边缘类分布。它有助于模型产生不同的预测,特别是对于几乎没有监督的设置(Sohn et al., 2020),因此收敛更快,泛化更好。
FreeMatch在第t次迭代时的总体目标是:
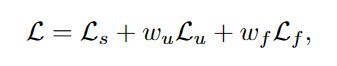
实验:
伪代码如下:
