TransE 及其实现

1. What is TransE?

TransE (Translating Embedding), an energy-based model for learning low-dimensional embeddings of entities.

核心思想：将 relationship 视为一个在 embedding space 的 translation。如果 (h, l, t) 存在，那么 $h+l\approx t$。

Motivation：一是在 Knowledge Base 中，层次化的关系是非常常见的，translation 是一种很自然的用来表示它们的变换；二是近期一些从 text 中学习 word embedding 的研究发现，一些不同类型的实体之间的 1-to-1 的 relationship 可以被 model 表示为在 embedding space 中的一种 translation。

2. Learning TransE

TransE 的训练算法如下：

2.1 输入参数

• training set $S$：用于训练的三元组的集合，entity 的集合为 $E$，rel. 的集合为 $L$
• margin $\gamma$：损失函数中的间隔，这个在原 paper 中描述很模糊
• 每个 entity 或 rel. 的 embedding dim $k$

2.2 训练过程

初始化：对每一个 entity 和 rel. 的 embedding vector 用 xavier_uniform 分布来初始化，然后对它们实施 L1 or L2 正则化。

loop：

• 在 entity embedding 被更新前进行一次归一化，这是通过人为增加 embedding 的 norm 来防止 loss 在训练过程中极小化。
• sample 出一个 mini-batch 的正样本集合
  S
  b
  a
  t
  c
  h
  S_{batch}
  Sbatch​
• 将
  T
  b
  a
  t
  c
  h
  T_{batch}
  Tbatch​ 初始化为空集，它表示本次 loop 用于训练 model 的数据集
• for
  (
  h
  ,
  l
  ,
  t
  )
  ∈
  S
  b
  a
  t
  c
  h
  (h,l,t) \in S_{batch}
  (h,l,t)∈Sbatch​ do:
  • 根据 (h, l, t) 构造出一个错误的三元组
    (
    h
    ′
    ,
    l
    ,
    t
    ′
    )
    (h', l, t')
    (h′,l,t′)
  • 将 positive sample $(h,l,t)$ 和 negative sample
    (
    h
    ′
    ,
    l
    ,
    t
    ′
    )
    (h',l,t')
    (h′,l,t′) 加入到
    T
    b
    a
    t
    c
    h
    T_{batch}
    Tbatch​ 中
• 计算
  T
  b
  a
  t
  c
  h
  T_{batch}
  Tbatch​ 每一对 positive sample 和 negative sample 的 loss，然后累加起来用于更新 embedding matrix。每一对的 loss 计算方式为：
  l
  o
  s
  s
  =
  [
  γ
  +
  d
  (
  h
  +
  l
  ,
  t
  )
  −
  d
  (
  h
  ′
  +
  l
  ,
  t
  ′
  )
  ]
  +
  loss = [\gamma + d(h+l,t) - d(h'+l,t')]_+
  loss=[γ+d(h+l,t)−d(h′+l,t′)]+​

这个过程中，triplet 的 energy 就是指的 $d(h+l,t)$，它衡量了 $h+l$ 与 $t$ 的距离，可以采用 L1 或 L2 norm，即 $||h+r-t||$ 具体计算方式可见代码实现。

loss 的计算中，
[
x
]
+
=
max
⁡
(
,
x
)
[x]_+ = \max(0,x)
[x]+​=max(0,x)。

关于 margin $\gamma$ 的含义， 它相当于是一个正确 triple 与错误 triple 之前的间隔修正，margin 越大，则两个 triple 之前被修正的间隔就越大，则对于 embedding 的修正就越严格。我们看
l
o
s
s
=
[
γ
+
d
(
h
+
l
,
t
)
−
d
(
h
′
+
l
,
t
′
)
]
+
loss = [\gamma + d(h+l,t) - d(h'+l,t')]_+
loss=[γ+d(h+l,t)−d(h′+l,t′)]+​，我们希望是 $d(h+l,t)$ 越小越好，
d
(
h
′
+
l
,
t
′
)
d(h'+l,t')
d(h′+l,t′) 越大越好，假设 $d(h+l,t)$ 处于理想情况下等于 0，那么由于 $\gamma$ 的存在，
d
(
h
′
+
l
,
t
′
)
d(h'+l,t')
d(h′+l,t′) 如果不是很大的话，仍然会产生 loss，只有当
d
(
h
′
+
l
,
t
′
)
d(h'+l,t')
d(h′+l,t′) 大于 $\gamma$ 时才会让 loss = 0，所以 $\gamma$ 越大，对 embedding 的修正就越严格。

错误三元组的构造方法：将 $(h,l,t)$ 中的头实体、关系和尾实体其中之一随机替换为其他实体或关系来得到。

2.3 评价指标

链接预测是用来预测三元组 (h,r,t) 中缺失实体 h, t 或 r 的任务，对于每一个缺失的实体，模型将被要求用所有的知识图谱中的实体作为候选项进行计算，并进行排名，而不是单纯给出一个最优的预测结果。

1. Mean rank - 正确三元组在测试样本中的得分排名，越小越好

首先对于每个 testing triple，以预测 tail entity 为例，我们将 $(h,r,t)$ 中的 t 用 KG 中的每个 entity 来代替，然后通过
f
r
(
h
,
t
)
f_r(h,t)
fr​(h,t) 来计算分数，这样就可以得到一系列的分数，然后将这些分数排列。我们知道 f 函数值越小越好，那么在前面的排列中，排地越靠前越好。重点来了，我们去看每个 testing triple 中正确答案（也就是真实的 t）在上述序列中排多少位，比如
t
1
t_1
t1​ 排 100，
t
2
t_2
t2​ 排 200，
t
3
t_3
t3​ 排 60 …，之后对这些排名求平均，就得到 mean rank 值了。

2. Hits@10 - 得分排名前 n 名的三元组中，正确三元组的占比，越大越好

还是按照上述进行 f 函数值排列，然后看每个 testing triple 正确答案是否排在序列的前十，如果在的话就计数 +1，最终 (排在前十的个数) / (总个数) 就等于 Hits@10。

在原论文中，由于这个 model 比较老了，其 baseline 也没啥参考性，就不做研究了，具体的实验可参考论文。

3. TransE 优缺点

优点：与以往模型相比，TransE 模型参数较少，计算复杂度低，却能直接建立实体和关系之间的复杂语义联系，在 WordNet 和 Freebase 等 dataset 上较以往模型的 performance 有了显著提升，特别是在大规模稀疏 KG 上，TransE 的性能尤其惊人。

缺点：在处理复杂关系（1-N、N-1 和 N-N）时，性能显著降低，这与 TransE 的模型假设有密切关系。假设有 (美国，总统，奥巴马）和（美国，总统，布什），这里的“总统”关系是典型的 1-N 的复杂关系，如果用 TransE 对其进行学习，则会有：

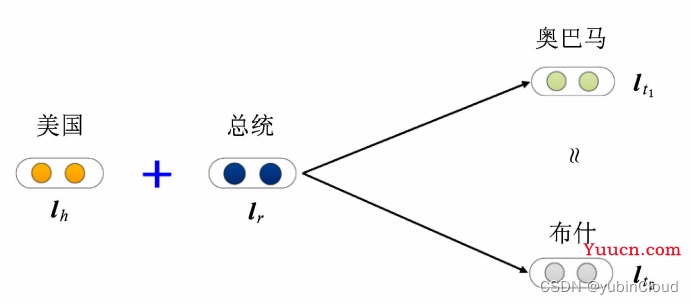
那么这将会使奥巴马和布什的 vector 变得相同。所以由于这些复杂关系的存在，导致 TransE 学习得到的实体表示区分性较低。

4. TransE 实现

这里选择用 pytorch 来实现 TransE 模型。

4.1 __init__ 函数

其参数有：

• ent_num：entity 的数量
• rel_num：relationship 的数量
• dim：每个 embedding vector 的维度
• norm：在计算 $d(h+l,t)$ 时是使用 L1 norm 还是 L2 norm，即
  d
  (
  h
  +
  l
  ,
  t
  )
  =
  ∣
  ∣
  h
  +
  l
  −
  t
  ∣
  ∣
  L
  1
   
  o
  r
   
  L
  2
  d(h+l,t)=||h+l-t||_{L1 \ or \ L2}
  d(h+l,t)=∣∣h+l−t∣∣L1 or L2​
• margin：损失函数中的间隔，是个 hyper-parameter
• $\alpha$：损失函数计算中的正则化项参数

class TransE(nn.Module):
    def __init__(self, ent_num, rel_num, device, dim=100, norm=1, margin=2.0, alpha=0.01):
        super(TransE, self).__init__()
        self.ent_num = ent_num
        self.rel_num = rel_num
        self.device = device
        self.dim = dim
        self.norm = norm # 使用L1范数还是L2范数
        self.margin = margin
        self.alpha = alpha
        # 初始化实体和关系表示向量
        self.ent_embeddings = nn.Embedding(self.ent_num, self.dim)
        torch.nn.init.xavier_uniform_(self.ent_embeddings.weight.data)
        self.ent_embeddings.weight.data = F.normalize(self.ent_embeddings.weight.data, 2, 1)
        self.rel_embeddings = nn.Embedding(self.rel_num, self.dim)
        torch.nn.init.xavier_uniform_(self.rel_embeddings.weight.data)
        self.rel_embeddings.weight.data = F.normalize(self.rel_embeddings.weight.data, 2, 1)
        # 损失函数
        self.criterion = nn.MarginRankingLoss(margin=self.margin)

初始化 embedding matrix 时，直接用 nn.Embedding 来完成，参数分别是 entity 的数量和每个 embedding vector 的维数，这样得到的就是一个 ent_num * dim 大小的 Embedding Matrix。

torch.nn.init.xavier_uniform_ 是一个服从均匀分布的 Glorot 初始化器，在这里做的就是对 Embedding Matrix 中每个位置填充一个 xavier_uniform 初始化的值，这些值从均匀分布 $U(-a,a)$ 中采样得到，这里的 $a$ 是：

a
=
g
a
i
n
×
6
f
a
n
_
i
n
+
f
a
n
_
o
u
t
a = gain \times \sqrt{\frac{6}{fan\_in + fan\_out}}
a=gain×fan_in+fan_out6​​

在这里，对于 Embedding 这样的二维矩阵来说，fan_in 和 fan_out 就是矩阵的长和宽，gain 默认为 1。其完整具体行为可参考 pytorch 初始化器文档。

F.normalize(self.ent_embeddings.weight.data, 2, 1) 这一步就是对 ent_embeddings 的每一个值除以 dim = 1 上的 2 范数值，注意 ent_embeddings.weight.data 的 size 是 (ent_num, embs_dim)。具体来说就是这一步把每行都除以该行下所有元素平方和的开方，也就是 $l\leftarrow l/||l||$。

损失函数这里先跳过，之后计算损失的步骤一同来看。

4.2 从 ent_idx 到 ent_embs

由于 network 的输入是 ent_idx，因此需要将其根据 embedding matrix 转换成 ent_embs。我们通过 get_ent_resps 函数来完成，其实就是个静态查表的操作：

class TransE(nn.Module):
	...
	def get_ent_resps(self, ent_idx): #[batch]
        return self.ent_embeddings(ent_idx) # [batch, emb]

4.3 计算 energy $d(h+l,t)$

它衡量了 $h+l$ 与 $t$ 的距离，可以采用 L1 或 L2 norm 来算，具体采用哪个由 __init__ 函数中的 self.norm 来决定：

class TransE(nn.Module):
	...
	def distance(self, h_idx, r_idx, t_idx):
        h_embs = self.ent_embeddings(h_idx) # [batch, emb]
        r_embs = self.rel_embeddings(r_idx) # [batch, emb]
        t_embs = self.ent_embeddings(t_idx) # [batch, emb]
        scores = h_embs + r_embs - t_embs
		# norm 是计算 loss 时的正则化项
        norms = (torch.mean(h_embs.norm(p=self.norm, dim=1) - 1.0)
                 + torch.mean(r_embs ** 2) +
                 torch.mean(t_embs.norm(p=self.norm, dim=1) - 1.0)) / 3
        return scores.norm(p=self.norm, dim=1), norms

4.4 计算 loss

self.criterion 是通过实例化 MarginRankingLoss 得到的，这个类的初始化接收 margin 参数，实例化得到 self.criterion，其计算方式如下：

c
r
i
t
e
r
i
o
n
(
x
1
,
x
2
,
y
)
=
max
⁡
(
,
−
y
×
(
x
1
−
x
2
)
+
m
a
r
g
i
n
)
criterion(x_1,x_2,y) = \max(0, -y \times (x_1 - x_2) + margin)
criterion(x1​,x2​,y)=max(0,−y×(x1​−x2​)+margin)

借助于此，我们可以实现计算 loss 的代码：

class TransE(nn.Module):
	...
	def loss(self, positive_distances, negative_distances):
        target = torch.tensor([-1], dtype=torch.float, device=self.device)
        return self.criterion(positive_distances, negative_distances, target)

positive_distances 就是 $d(h+l,t)$，negative_distances 就是
d
(
h
′
+
l
,
t
′
)
d(h'+l, t')
d(h′+l,t′)，target = [-1]，代入 criterion 的计算公式就是我们计算 一对正样本和负样本的 loss 了。

4.5 forward

class TransE(nn.Module):
	...
	def forward(self, ph_idx, pr_idx, pt_idx, nh_idx, nr_idx, nt_idx):
        pos_distances, pos_norms = self.scoring(ph_idx, pr_idx, pt_idx)
        neg_distances, neg_norms = self.scoring(nh_idx, nr_idx, nt_idx)
        tmp_loss = self.loss(pos_distances, neg_distances)
        tmp_loss += self.alpha * pos_norms   # 正则化项
        tmp_loss += self.alpha * neg_norms   # 正则化项
        return tmp_loss, pos_distances, neg_distances

以上我们讲完了 TransE 模型的定义，接下来就是讲对 TransE 模型的训练了，只要理解了 TransE 模型的定义，其训练应该不是难事。