- 英文标题:Transferability in Deep Learning: A Survey
- 中文标题:深度学习中的可迁移性综述
- 论文下载链接:arxiv@2201.05867
序言
这篇综述整体来说还是比较详实的,迁移学习本身在人工智能中的应用是非常广泛的,因此很容易与其他方法相结合,原文第三大节关于适应性的部分是非常关键的,也是本笔注的重点内容,理论性极强,其他两部分相对要水一些,很多老生常谈的东西就不作记录了。个人感觉是比较适合有一定机器学习基础,然后希望巩固迁移学习相关知识的人进行阅读理解。
摘要
The success of deep learning algorithms generally depends on large-scale data, while humans appear to have inherent ability of knowledge transfer, by recognizing and applying relevant knowledge from previous learning experiences when encountering and solving unseen tasks. Such an ability to acquire and reuse knowledge is known as transferability in deep learning. It has formed the long-term quest towards making deep learning as data-efficient as human learning, and has been motivating fruitful design of more powerful deep learning algorithms. We present this survey to connect different isolated areas in deep learning with their relation to transferability, and to provide a unified and complete view to investigating transferability through the whole lifecycle of deep learning. The survey elaborates the fundamental goals and challenges in parallel with the core principles and methods, covering recent cornerstones in deep architectures, pre-training, task adaptation and domain adaptation. This highlights unanswered questions on the appropriate objectives for learning transferable knowledge and for adapting the knowledge to new tasks and domains, avoiding catastrophic forgetting and negative transfer. Finally, we implement a benchmark and an open-source library, enabling a fair evaluation of deep learning methods in terms of transferability.
文章目录
- 序言
-
- 摘要
- 1 导论 Introduction
-
- 1.1 术语 Terminology
- 1.2 概述 Overview
- 2 预训练 Pre-Training
-
- 2.1 预训练模型 Pre-Training Model
- 2.2 有监督的预训练模型 Supervised Pre-training Model
-
- 2.2.1 元学习 Meta Learning
- 2.2.2 因果学习 Casual Learning
- 2.3 无监督的预训练模型
-
- 2.3.1 生成学习 Generative Learning
- 2.3.2 对比学习 Contrastive Learning
- 2.4 注释 Remarks
- 3 适应性 Adaptation
-
- 3.1 任务适应性 Task Adaptation
-
- 3.1.1 灾难性遗忘 Catastrophic Forgetting
- 3.1.2 负迁移 Negative Transfer
- 3.1.3 参数功效 Parameter Efficiency
- 3.1.4 数据功效 Data Efficiency
- 3.1.5 注释 Remarks
- 3.2 领域适应性 Domain Adaptation
-
- 3.2.1 统计匹配 Statistics Matching
- 3.2.2 领域对立学习 Domain Adversarial Learning
- 3.2.3 假设对立学习 Hypothesis Adversarial Learning
- 3.2.4 领域翻译 Domain Translation
- 3.2.5 半监督学习 Semi-Supervised Learning
- 3.2.6 注释 Remarks
- 4 评估 Evaluation
-
- 4.1 数据集 Datasets
- 4.2 开源包 Library
- 4.3 基准 Benchmark
-
- 4.3.1 预训练 Pre-Training
- 4.3.2 任务适应性 Task Adaptation
- 4.3.3 领域适应性 Domain Adaptation
- 5 结论 Conclusion
- 参考文献
1 导论 Introduction
-
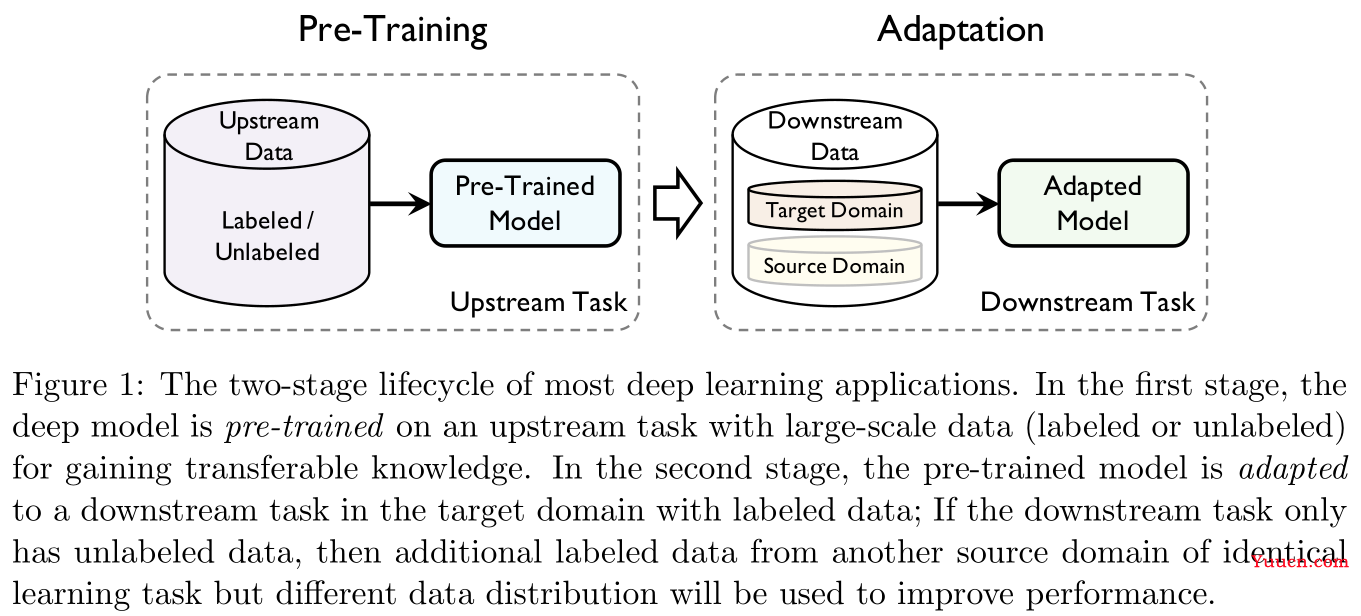
预训练本身就是一种迁移学习。
-
迁移学习分为两阶段:预训练(pre-training)与适应(adaptation)。前者关注一般的可迁移性(generic transferability),后者关注具体的可迁移性(specific transferability)。
1.1 术语 Terminology
| 数学标记 | 具体含义 |
|---|---|
X \mathcal X X |
输入空间 |
Y \mathcal Y Y |
输出空间 |
f f f |
f : X → Y f:\mathcal X\rightarrow \mathcal Y f:X→Y是需要学习的标注函数 |
l l l |
l : Y × Y → R + l:\mathcal{Y}\times \mathcal{Y}\rightarrow \R_+ l:Y×Y→R+是给定的损失函数 |
D \mathcal D D |
X \mathcal X X上的某个未知分布 |
D ^ \mathcal{\hat D} D |
独立同分布采样自 D \mathcal D D的样本 { x 1 , . . . , x n } \{{\bf x}_1,...,{\bf x}_n\} {x1,...,xn} |
P ( ⋅ ) P(\cdot) P(⋅) |
定义在 X \mathcal X X上的事件概率 |
E ( ⋅ ) \mathbb E(\cdot) E(⋅) |
随机变量数学期望 |
U \mathcal U U |
上游数据 |
S \mathcal S S |
下游数据的源领域 |
T \mathcal T T |
下游数据的目标领域 |
t ∗ t_{*} t∗ |
∗ * ∗领域的任务, ∗ * ∗可以取 T , S , U \mathcal{T,S,U} T,S,U |
H \mathcal H H |
假设空间(可以理解为模型集合) |
h h h |
假设空间中的一个假设(下文中如不作特殊说明,假设和模型含义相同) |
ψ \psi ψ |
特征生成器 |
θ \theta θ |
假设参数 |
x \bf x x |
模型输入 |
y \bf y y |
模型输出 |
z \bf z z |
隐层特征激活生成结果 |
D D D |
用于区分不同分布的辨识器 |
定义
1
1
1(可迁移性):给定源领域
S
\mathcal{S}
S的学习任务
t
S
t_{\mathcal{S}}
tS以及目标领域
T
\mathcal T
T的学习任务
t
T
t_{\mathcal{T}}
tT,可迁移性(transferability)指从
t
S
t_{\mathcal S}
tS中获取可迁移的知识,将获取到的知识在
t
T
t_{\mathcal T}
tT中进行重用并能够使得
t
T
t_{\mathcal T}
tT的泛化误差降低,其中
S
≠
T
\mathcal S\neq \mathcal T
S=T或
t
S
≠
t
T
t_{\mathcal S}\neq t_{\mathcal T}
tS=tT。
1.2 概述 Overview
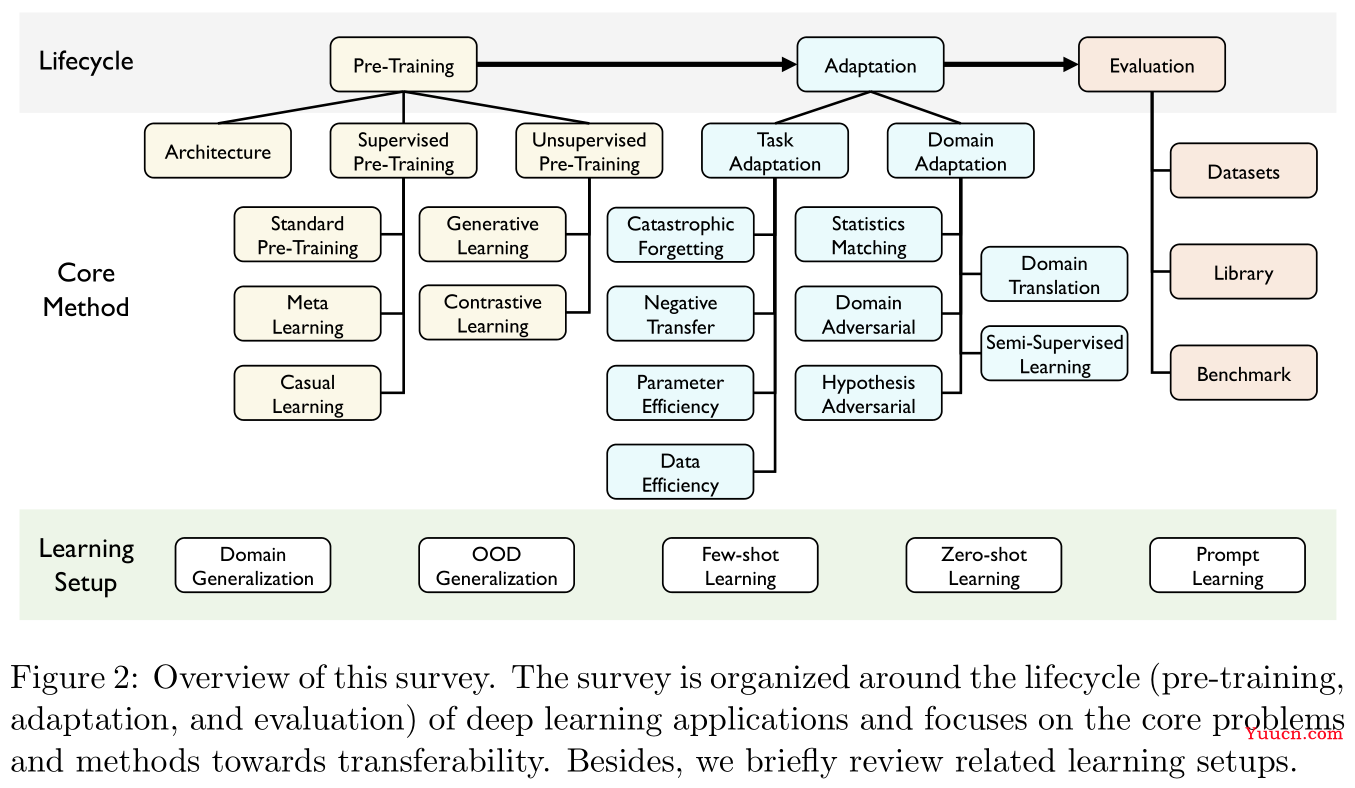
本文分三部分展开:
- 预训练(Pre-training):关于一些重要的迁移模型架构,有监督的预训练与无监督的预训练方法综述。这部分相对浅显,只对重点内容进行摘要记录。
- 适应性(Adaptation):重点在任务适应性(task adaptation)与领域适应性(domain adaptation),这部分理论性极强,尤其是领域适应性部分汇总了大量的定理与统计结果,感觉就不是同一个人写的。
- 评估(Evaluation):本文提出一个开源包用于迁移学习的通用算法以及评估,项目地址在GitHub@TLlib
2 预训练 Pre-Training
2.1 预训练模型 Pre-Training Model
-
一般来说,预训练任务学习的好坏直接影响预训练模型在下游任务中的应用性能。
-
一般来说,预训练会在非常大量的数据集上进行,因此如RNN和CNN这种做了局部连接假设的模型架构通常不会被作为预训练模型架构(因为数据足够多,不需要简化模型架构),目前主流的基本伤都是基于Transformer的大规模预训练模型。相较于RNN和CNN,Transformer对输入数据的结构几乎不作任何假定,即可以用于处理更广泛的数据类型。
-
预训练模型在迁移学习中的发展历程(如Figure 3所示):
-
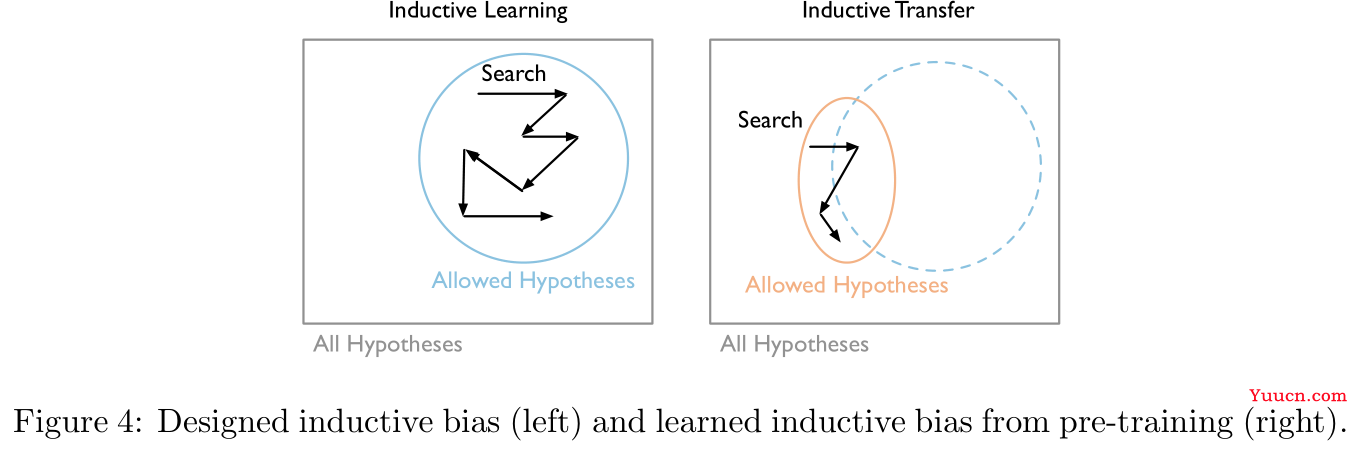
Figure 4中左图是直接训练时模型参数搜索的过程,右图是预训练迁移后的模型参数搜索过程,意思是说预训练的本质是缩小了模型参数的搜索范围(不过似乎也可以理解为是找到了一个更好的初始点):
2.2 有监督的预训练模型 Supervised Pre-training Model
-
有监督的预训练目的是在大规模标注数据上训练获得预训练模型,然后再迁移以增强下游任务(如Figure 5所示)。
-
标准的有监督的预训练在标注数据量重组的情况下是非常有用的,但是它有时候对于对立样本(adversarial examples)的存在是极其敏感的,这可能会影响迁移的鲁棒性。因此本部分将会着重介绍另外两种有监督的预训练方法。
2.2.1 元学习 Meta Learning
-
所谓元学习(meta-learning),通俗而言即学习如何学习,以提升迁移的效率。其核心在于将元知识(meta knowledge)
ϕ
\phi
ϕ与模型融合,元知识
ϕ
\phi
ϕ可以捕获不同学习任务的本质属性(intrinsic properties),又称为元训练(meta-training)。当需要解决一个新任务时,学习到的元知识救可以帮助目标模型参数
θ
\theta
θ快速适应到新任务中,这个过程称为元测试(meta-testing)。 -
如Figure 6所示,左图是为了模拟元测试过程中的快速适应条件,将元训练数据构造成一个由
n
n
n个学习任务组成的集合,每个任务分别对应一个学习任务
i
∈
[
n
]
i\in[n]
i∈[n],包含用于适应此任务的训练集
D
i
t
r
\mathcal{D}_i^{\rm tr}
Ditr和用于评估的测试集
D
i
t
s
\mathcal{D}_i^{\rm ts}
Dits,右图则是说明元训练的目标函数是一个二级优化问题:
ϕ
∗
=
argmax
ϕ
∑
i
=
1
n
log
P
(
θ
i
(
ϕ
)
∣
D
i
t
s
)
,
where
θ
i
(
ϕ
)
=
argmax
θ
log
P
(
θ
∣
D
i
t
r
,
ϕ
)
(1)
\phi^*=\text{argmax}_{\phi}\sum_{i=1}^n\log P(\theta_i(\phi)|\mathcal{D}_i^{\rm ts}),\quad\text{where }\theta_i(\phi)=\text{argmax}_{\theta}\log P(\theta|\mathcal{D}_i^{\rm tr},\phi)\tag{1}
ϕ∗=argmaxϕi=1∑nlogP(θi(ϕ)∣Dits),where θi(ϕ)=argmaxθlogP(θ∣Ditr,ϕ)(1)
这里内层优化用于更新模型参数
θ
\theta
θ,外层优化用于寻找更好的元知识用于迁移,元学习的关键就在于如何构建元知识的形式。
-
基于内存的元学习(memory-based meta-learning):
控制器将从训练数据
D
i
t
r
\mathcal{D}_i^{\rm tr}
Ditr中挖掘得到的知识写入内存,并从内存中读取知识以使用基础学习器
θ
\theta
θ在测试数据
D
i
t
r
\mathcal{D}_i^{\rm tr}
Ditr上进行预测,控制器的参数将不断更新。感觉上这个并不是什么很新奇的方法,本质上你在做项目时预先存好的一些预处理数据都可以视为是基于内存的元学习。如参考文献
[
150
]
[150]
[150]提出的内存增强神经网络(memory-augmented neural networks,MANN)将绑定样本表示类信息(bound sample representation-class label information)存储在外部内存中,以用于检索作为特征来进行预测。参考文献
[
121
]
[121]
[121]则是提出另一种内存机制,基础学习器用于提供关于当前任务的状态,元学习器则与外部内存交互以生成用于基础学习器的模型参数,以快速学习新任务。基于内存的元学习对于如少射分类(few-shot classification)以及强化学习的下游任务是比较有优势的,但是需要设计黑盒架构来合并内存机制,往往我们并不知道到底存储了什么东西,以及为什么存储的东西是有益于模型迁移的。
-
基于优化的元学习(optimization-based meta-learning):
这种方法考察的是将模型较好的初始化作为元知识。如参考文献
[
43
]
[43]
[43]中提出的模型不可知元学习(model-agnostic meta-learning,MAML)直接寻找一个最适合迁移微调的初始化,即只需要少量梯度下降迭代以及少量标注数据即可适应到新任务中。为了学习这样的一个初始化,对于每一个样本任务
i
∈
[
n
]
i\in[n]
i∈[n],模型
ϕ
\phi
ϕ首先其训练数据
D
i
t
r
\mathcal{D}_i^{\rm tr}
Ditr上进行一次步长为
α
\alpha
α的梯度下降迭代:
θ
i
=
ϕ
−
α
∇
ϕ
L
(
ϕ
,
D
i
t
r
)
(2)
\theta_i=\phi-\alpha\nabla_{\phi}L(\phi,\mathcal{D}_i^{\rm tr})\tag{2}
θi=ϕ−α∇ϕL(ϕ,Ditr)(2)这是在模仿从
ϕ
\phi
ϕ这个点开始对模型进行微调。作为元知识,
ϕ
\phi
ϕ应当具有良好的可迁移性,因此对于所有任务
i
∈
[
n
]
i\in[n]
i∈[n],经过微调的参数
θ
i
\theta_i
θi在测试集
D
i
t
s
\mathcal{D}_i^{\rm ts}
Dits上的表现应当很好:
min
ϕ
∑
i
=
1
n
L
(
θ
i
(
ϕ
)
,
D
i
t
s
)
=
∑
i
=
1
n
L
(
ϕ
−
−
α
∇
ϕ
L
(
ϕ
,
D
i
t
r
)
,
D
i
t
s
)
(3)
\min_{\phi}\sum_{i=1}^nL(\theta_i(\phi),\mathcal{D}_i^{\rm ts})=\sum_{i=1}^nL(\phi--\alpha\nabla_{\phi}L(\phi,\mathcal{D}_i^{\rm tr}),\mathcal{D}_i^{\rm ts})\tag{3}
ϕmini=1∑nL(θi(ϕ),Dits)=i=1∑nL(ϕ−−α∇ϕL(ϕ,Ditr),Dits)(3)注意道MAML的元知识维数太高,因此参考文献
[
167
]
[167]
[167]使用标准的预训练作为初始化来进行改进。另外,参考文献
[
137
,
145
,
196
]
[137,145,196]
[137,145,196]也对MAML进行了一定改进。 -
元学习的表现并不稳定,有时候会比标准的预训练方法更差。
2.2.2 因果学习 Casual Learning
因果学习(casual learning)旨在对分布外的(out-of-distribution,OOD)领域进行外推式的(extrapolated)迁移学习。其核心是使用某种因果机制(causal mechanisms)来捕获复杂真实世界的分布,当分布发生变化时,只有少数因果机制发生变化,而其余保持不变,这样即可得到更好的OOD推广。具体如Figure 7所示:
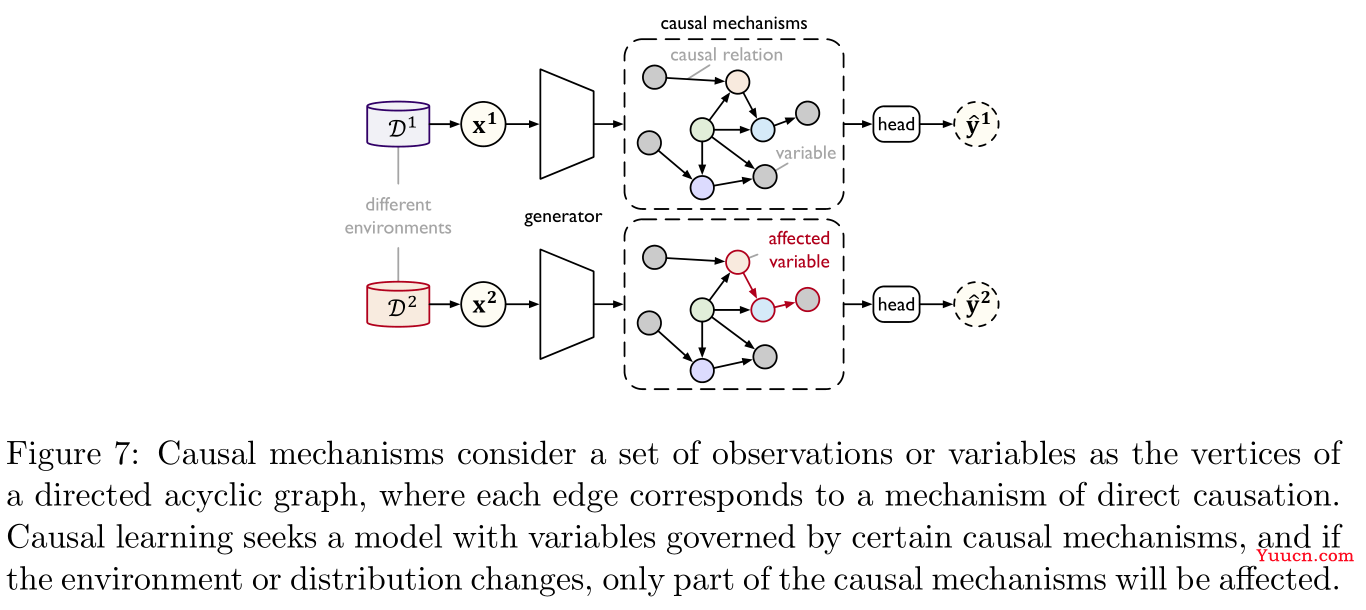
因果机制由一张有向无环图中的顶点作为变量表示,每一条边表示了某种因果关系,这样就可以在给定父节点分布的条件下,得到每个变量的联合分布的非纠缠因子分解(disentangled factorization)形式,此时分布上的一些小变化只会对非纠缠因子分解的局部或者以一种稀疏的方式进行影响。因果学习的关键问题是获取由独立因果机制控制的变量,下面是两种常用的方法:
-
模块化模型(modular model):参考文献
[
56
,
31
]
[56,31]
[56,31],简而言之就是使用LSTM或者GRU来作为因果机制的表示模块。 -
不变学习(invariant learning):参考文献
[
129
,
4
]
[129,4]
[129,4],这里介绍后一篇参考文献
[
4
]
[4]
[4]的方法,给定数据表示
ψ
:
X
→
Z
\psi:\mathcal{X\rightarrow Z}
ψ:X→Z,以及训练环境
E
t
r
\mathcal{E}^{\rm tr}
Etr,表示与输出的条件概率是不变的若有一个分类器
h
:
Z
→
Y
h:\mathcal{Z\rightarrow Y}
h:Z→Y同时对于所有环境都是最优的。着可以表示为下面带约束的优化问题:
minimize
ψ
:
X
→
Z
,
h
:
Z
→
Y
∑
e
∈
E
t
r
ϵ
e
(
h
∘
ψ
)
subject to
h
∈
argmin
h
ˉ
:
Z
→
Y
ϵ
e
(
h
∘
ψ
)
,
∀
e
∈
E
t
r
(4)
\begin{aligned} &\text{minimize}_{\psi:\mathcal{X\rightarrow Z},h:\mathcal{Z\rightarrow Y}}&&\sum_{e\in\mathcal{E}^{\rm tr}}\epsilon^{e}(h\circ\psi)\\ &\text{subject to}&&h\in\text{argmin}_{\bar h:\mathcal{Z\rightarrow Y}}\epsilon^{e}(h\circ\psi),\forall e\in\mathcal{E}^{\rm tr} \end{aligned}\tag{4}
minimizeψ:X→Z,h:Z→Ysubject toe∈Etr∑ϵe(h∘ψ)h∈argminhˉ:Z→Yϵe(h∘ψ),∀e∈Etr(4)
其中
ϵ
e
(
h
∘
ψ
)
\epsilon^{e}(h\circ\psi)
ϵe(h∘ψ)表示在环境
e
e
e中预测器
h
∘
ψ
h\circ \psi
h∘ψ的期望误差。
2.3 无监督的预训练模型
无监督预训练主要是指自监督学习(self-supervised learning),重点在于如何构建自监督学习任务用于预训练,方法主要可以分为生成学习(generative learning)与对比学习(contrastive learning)两大类。
2.3.1 生成学习 Generative Learning
-
如Figure 8所示,生成学习中采用一个编码器
f
θ
f_{\theta}
fθ将扰乱的输入
x
~
\bf \tilde x
x~映射到隐层表示
z
=
f
θ
(
x
~
)
{\bf z}=f_{\theta}({\bf \tilde x})
z=fθ(x~),一个解码器
g
θ
g_{\theta}
gθ将表示重构为一个估计输入
x
^
=
g
θ
(
z
)
{\bf \hat x}=g_{\theta}({\bf z})
x=gθ(z),模型通过最小化重构误差
L
g
e
n
(
x
^
,
x
)
L_{\rm gen}({\bf \hat x},{\bf x})
Lgen(x,x)进行训练。这样做的目的是为了赋予模型以生成数据分布的能力。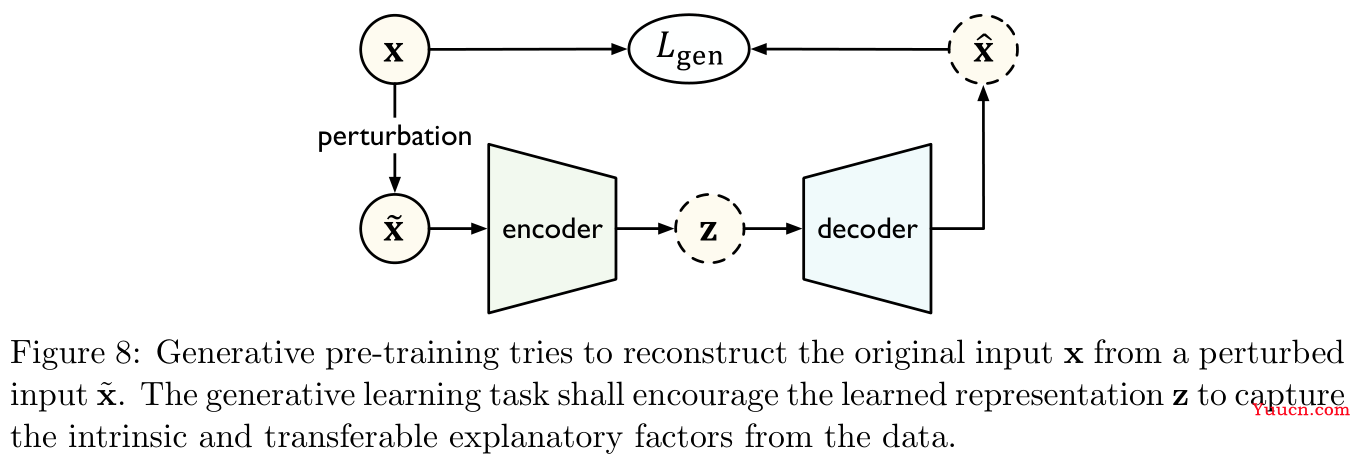
-
生成学习方法可以分为两类:自回归模型(auto-regressive)与自编码模型(auto-encoding)。
-
自回归模型:老生常谈,如Figure 9所示,典型的语言模型及其若干变体就属于自回归模型。
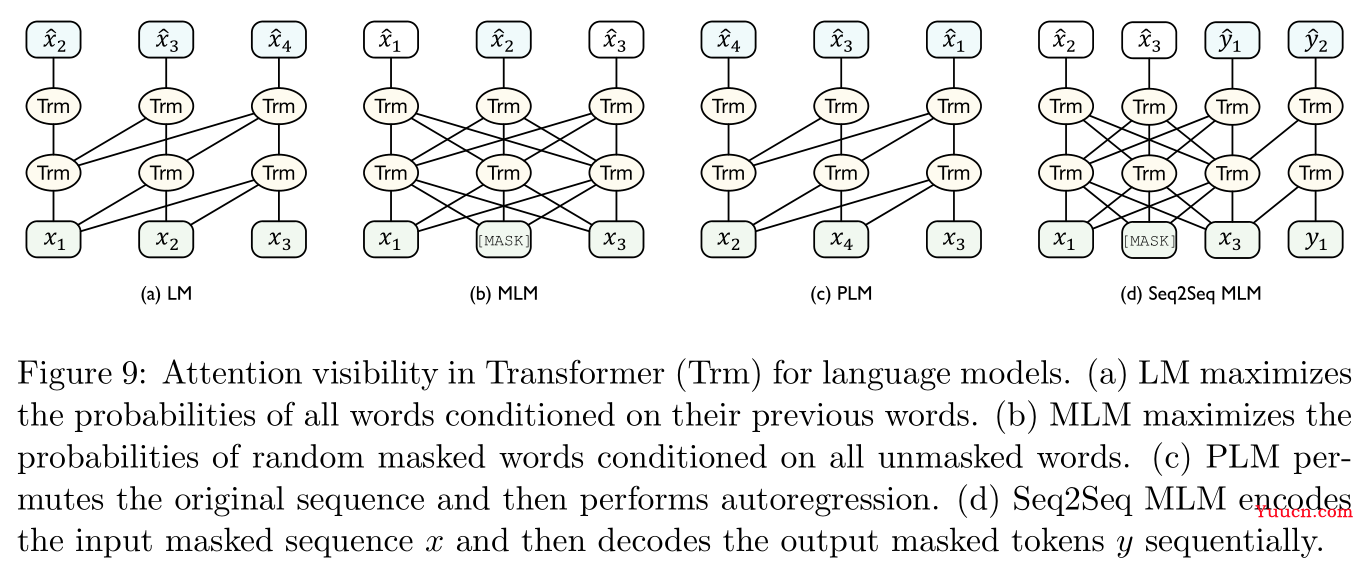
给定文本序列
x
1
:
T
=
[
x
1
,
.
.
,
x
T
]
{\bf x}_{1:T}=[x_1,..,x_T]
x1:T=[x1,..,xT],语言模型的训练目标是最大化每个分词的条件概率:
max
θ
∑
t
=
1
T
log
P
θ
(
x
t
∣
x
t
−
k
,
.
.
.
,
x
t
−
1
)
(5)
\max_{\theta}\sum_{t=1}^T\log P_{\theta}(x_t|x_{t-k},...,x_{t-1})\tag{5}
θmaxt=1∑TlogPθ(xt∣xt−k,...,xt−1)(5)
经典的GPT模型(参考文献
[
134
]
[134]
[134])即属于自回归模型。 -
自编码模型:思想是根据编码表示生成原始数据来近似数据分布,常见的BERT模型就属于自编码模型。
在Figure 9中的最后一张图中的掩盖语言模型(Masked Language Model,MLM,这个也是BERT模型训练中使用的机制),首先用
[
M
A
S
K
]
\rm [MASK]
[MASK]标记在输入语句
x
{\bf x}
x中随机掩盖掉一些分词
m
(
x
)
m({\bf x})
m(x),然后训练模型根据剩余的分词
x
\
m
(
x
)
{\bf x}_{\backslash m({\bf x})}
x\m(x)来预测这些掩盖掉分词:
max
θ
∑
x
∈
m
(
x
)
log
P
θ
(
x
∣
x
\
m
(
x
)
)
(6)
\max_{\theta}\sum_{x\in m({\bf x})}\log P_{\theta}(x|{\bf x}_{\backslash m({\bf x})})\tag{6}
θmaxx∈m(x)∑logPθ(x∣x\m(x))(6)
这种掩盖的思想是很常用的。 -
自回归自编码混合模型:
在Figure 9中的第三张图置换语言模型(permuted language model,PLM,参考文献
[
195
]
[195]
[195])首先随机地置换采样了语句序列地顺序,然后再在置换后的序列上进行自回归预测。其他的一些经典模型的训练也都采用了类似的方法(即既挖空,又改变顺序),比如T5模型(参考文献
[
136
]
[136]
[136]),RoBERTa(参考文献
[
109
]
[109]
[109]),ERNIE(参考文献
[
168
]
[168]
[168]),SpanBERT(参考文献
[
83
]
[83]
[83]),BART(参考文献
[
98
]
[98]
[98]),GPT-3(参考文献
[
18
]
[18]
[18]),多语言BERT(参考文献
[
132
]
[132]
[132]),XLM(参考文献
[
91
]
[91]
[91])。
-
2.3.2 对比学习 Contrastive Learning
-
如Figure 10所示,在对比学习中,有两个不同的视图(views),查询
x
q
{\bf x}^q
xq与键
x
k
{\bf x}^k
xk(由原始数据
x
{\bf x}
x构建得到),编码器将不同的视图映射到隐层表示,解码器则进一步将隐层表示映射到指标空间(metric space)。模型学习的目标是最小化同一个样本
x
{\bf x}
x的查询和键之间的距离。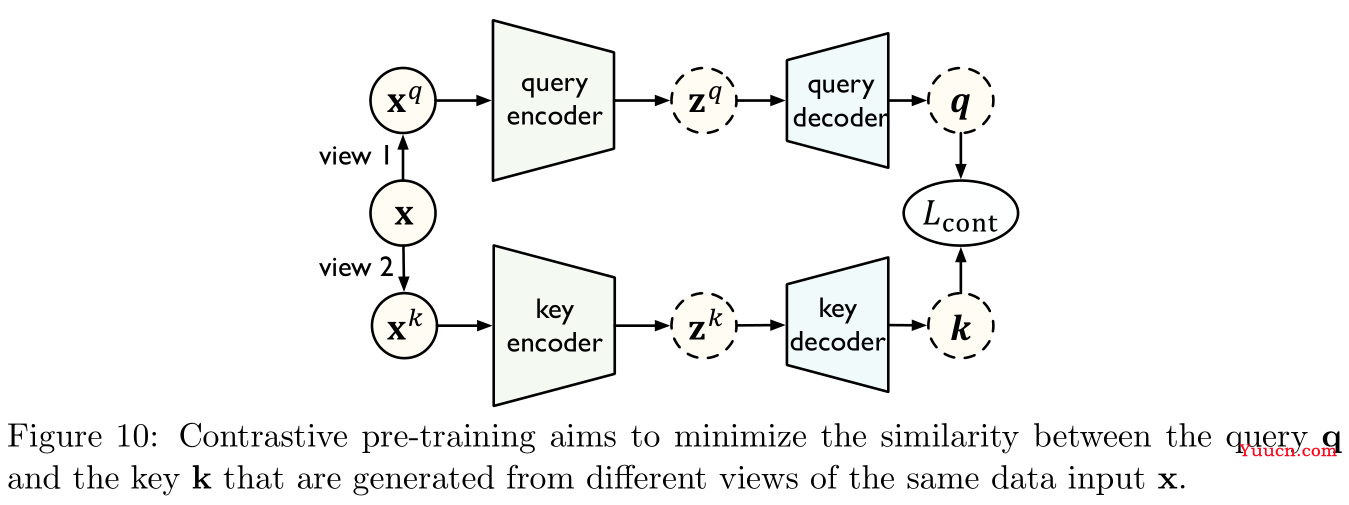
-
典型的对比学习方法:
-
互信息最大化(mutual information maximization):
以参考文献
[
70
]
[70]
[70]提出的深度信息最大化(Deep InfoMax)模型为例,它旨在从高级别的全局上下文以及低级别的局部特征之间的联系来学习得到可迁移的表示。具体而言,给定输入
x
{\bf x}
x,模型学习一个编码器
ψ
\psi
ψ来最大化
x
{\bf x}
x的输入输出之间的互信息,互信息可以通过训练一个区分器(discriminator)
D
D
D来区分它们联合分布与边际值(marginals)乘积来被估计与约束。通过使用噪声对比估计(noise-contrastive estimation,NCE)方法,模型的训练目标为:
max
ψ
E
x
∼
U
[
D
(
x
,
ψ
(
x
)
)
−
E
x
′
∼
U
~
(
log
∑
x
′
e
D
(
x
′
,
ψ
(
x
)
)
)
]
(7)
\max_{\psi}\mathbb{E}_{{\bf x}\sim\mathcal U}\left[D({\bf x},\psi({\bf x}))-\mathbb{E}_{{\bf x}'\sim\mathcal{\tilde U}}\left(\log\sum_{\bf x'}e^{D({\bf x}',\psi({\bf x}))}\right)\right]\tag{7}
ψmaxEx∼U[D(x,ψ(x))−Ex′∼U~(logx′∑eD(x′,ψ(x)))](7)
其中
x
\bf x
x是从上游任务的训练分布
U
\mathcal U
U中采样得到的输入样本,
x
′
\bf x'
x′是从另一个分布
U
~
=
U
\mathcal {\tilde U}=\mathcal U
U~=U中采样得到的样本,
D
D
D用于区分联合分布与边际值乘积。其余的一些相关工作包括参考文献
[
124
,
178
,
135
]
[124,178,135]
[124,178,135],最后一篇是处理零射问题的。 -
相关位置预测(relative position prediction):
这里主要讲的是下一句预测(next sentence prediction,NSP)任务,这个任务首次在BERT模型中使用,此后经典的ALBERT模型(参考文献
[
93
]
[93]
[93])也是使用的类似的预训练策略。 -
样例区分(instance discrimination):
这里介绍的是参考文献
[
191
]
[191]
[191]的InstDisc模型,旨在根据样例间的关系来学习可迁移的表示。具体而言,给定
n
n
n个样例,训练编码器
ψ
\psi
ψ用于区分不同的样例,即最小化同一样例的查询
q
\bf q
q与键
k
+
{\bf k}_+
k+之间的距离(这也称为整个样本),以及最大化不同样本之间的查询
q
\bf q
q与键
k
+
{\bf k}_+
k+之间的距离(这也称为负样本):
min
ψ
−
log
exp
(
q
⋅
k
+
/
τ
)
∑
j
=
K
exp
(
q
⋅
k
j
/
τ
)
(8)
\min_{\psi}-\log\frac{\exp({\bf q}\cdot{\bf k}_+/\tau)}{\sum_{j=0}^K\exp({\bf q}\cdot{\bf k}_j/\tau)}\tag{8}
ψmin−log∑j=0Kexp(q⋅kj/τ)exp(q⋅k+/τ)(8)
其中
τ
\tau
τ是一个超参数用于控制softmax值的偏移程度,
K
K
K是负样本的数量,其实这个就是负采样。如Figure 11所示,InstDisc模型使用了一个内存条(memory bank)来存储每个键最近更新的表示,由此增加了负样本的数量,可能会导致不一致的特征表示:
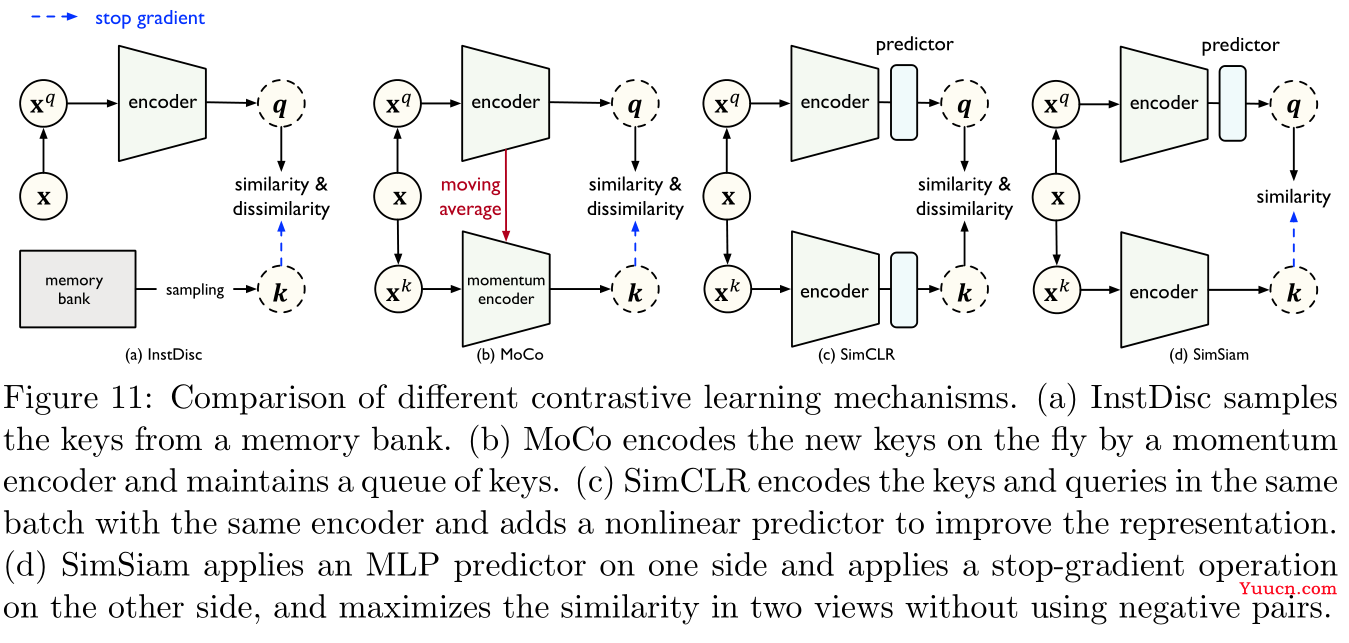
其他的一些相关研究包括参考文献
[
67
,
171
,
23
,
59
,
25
,
206
]
[67,171,23,59,25,206]
[67,171,23,59,25,206]
-
2.4 注释 Remarks
总结一下本小节所有方法的性能:
| 方法 | 模态延展性 | 任务延展性 | 数据功效 | 标注成本 |
|---|---|---|---|---|
| 标准预训练 | 优 | 中 | 优 | 差 |
| 元学习 | 优 | 差 | 差 | 差 |
| 因果学习 | 中 | 差 | 差 | 差 |
| 生成学习 | 中 | 优 | 优 | 优 |
| 对比学习 | 差 | 优 | 优 | 优 |
字段说明:
- 模态延展性(modality scalability):能否用于多模态数据,如文本、图片、音像。
- 任务延展性(task scalability):能否轻松的将预训练模型迁移到不同下游任务中。
- 数据功效(data efficiency):能否通过大规模预训练获得强有力的可迁移性。
- 标注成本(labeling cost):是否依赖手动数据标注。
3 适应性 Adaptation
3.1 任务适应性 Task Adaptation
所谓任务适应性(task adaptation),指给定一个预训练模型
h
θ
h_{\theta^0}
hθ0以及目标领域
T
^
=
{
x
i
,
y
i
}
i
=
1
m
\mathcal{\hat T}=\{{\bf x}_i,{\bf y}_i\}_{i=1}^m
T={xi,yi}i=1m(带标签的
m
m
m个样本对),我们的目的是据此在假设空间
H
\mathcal{H}
H中找到一个具体的假设
h
θ
:
X
→
Y
h_{\theta}:\mathcal X\rightarrow \mathcal Y
hθ:X→Y,使得风险
ϵ
T
(
h
θ
)
\epsilon_{\mathcal T}(h_{\theta})
ϵT(hθ)最小化。
一般而言,有两种方法将预训练模型适应到下游任务中:
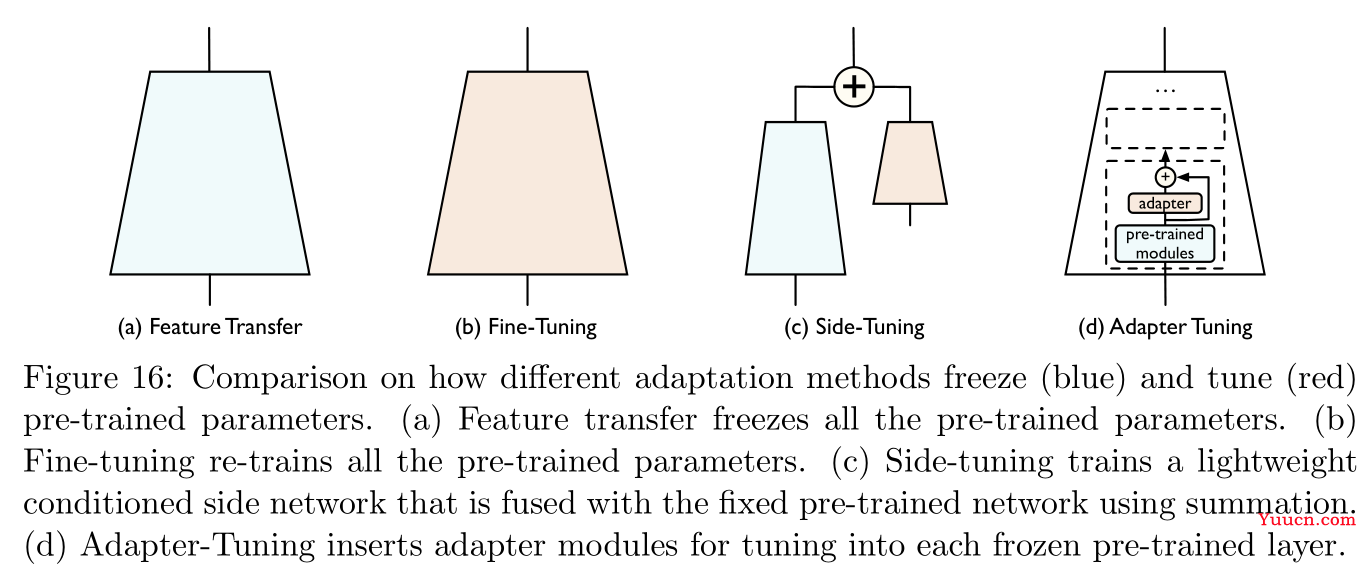
- 特征转换(feature transfer):此时预训练模型的网络层权重将被固定,只是再训练一个全连接网络用于输入特征转换。
- 微调(finetune):此时预训练模型的网络层权重相当于是模型训练的一个初始点,将继续在目标领域的样本对中继续训练优化其网络层权重。
特征转换操作便利、成本更小,但微调得到的模型性能通常会更好。
这里有一个概念叫作基准微调(vanilla finetune),即直接在目标数据上,根据经验风险最小化(empirical risk minimization)对预训练模型进行微调,但是这种方法将会受到灾难性遗忘(catastrophic forgetting)与负迁移(negative transfer)问题的困扰,Section 3.1.1与Section 3.1.2主要探讨的是如何缓解这两个问题。此外因为模型尺寸与训练数据量越来越庞大,Section 3.1.3与Section 3.1.4将探讨参数功效(parameter efficiency)与数据功效(data efficiency)的问题。
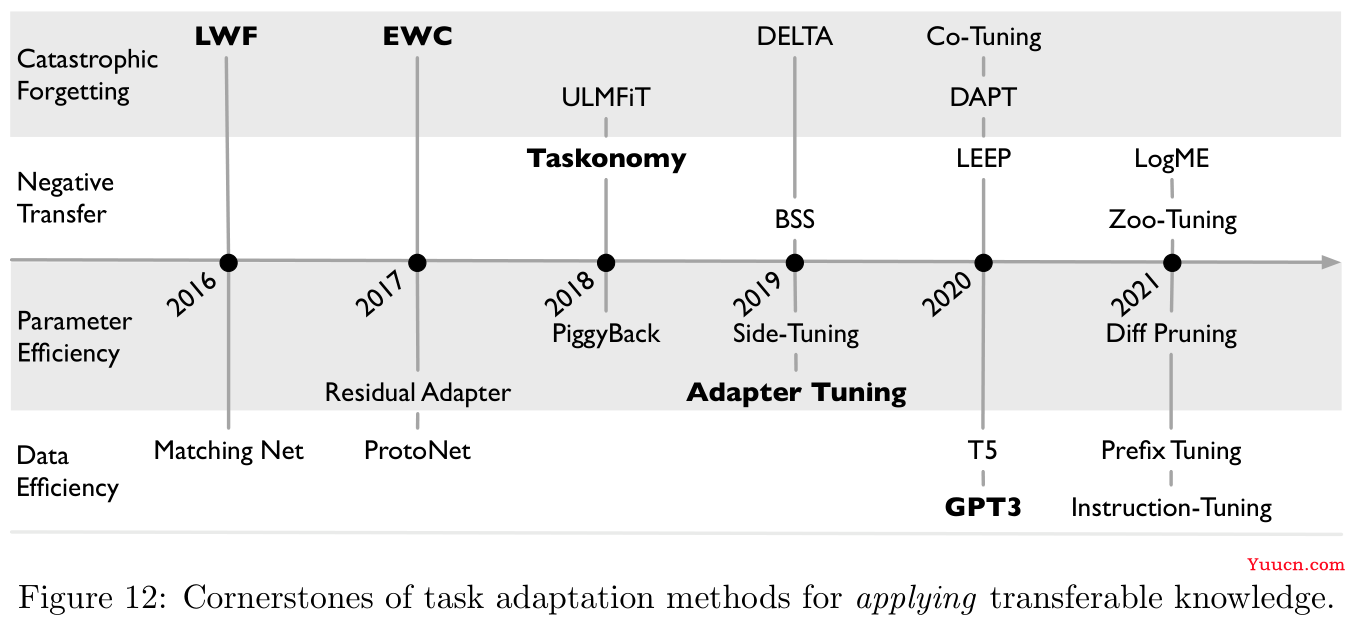
3.1.1 灾难性遗忘 Catastrophic Forgetting
-
灾难性遗忘的概念最早在终身学习(lifelong learning)中提出,指的是机器学习模型在新任务中训练时会逐渐损失从先前任务中学习到的知识(参考文献
[
86
]
[86]
[86])。 -
微调环节中,由于已标注数据的稀缺,可能会导致模型在目标数据上训练到过拟合,这种现象称为表征崩溃(representational collapse,参考文献
[
2
]
[2]
[2])。 -
传统的解决方案是训练模型时采用微小的学习率并采用早停(early-stopping)策略,但是容易使得模型陷入局部最优,一些比较新的研究方法:
- 参考文献
[
197
]
[197]
[197]:发现模型中不同网络层的可迁移性是有区别的,因此在迁移时对待不同网络层的训练方式应当有所区别; - 参考文献
[
112
]
[112]
[112]:基于上述发现,提出深度适应网络(deep adaptation network,DAN),这种网络架构中具体任务头(task-specific head)的的学习率是其他层的十倍; - 参考文献
[
74
]
[74]
[74]:从预训练模型的最后一层逐渐解冻(unfreeze)网络层权重直到第一层,这样可以有效地保留第一层中预训练的知识。 - 参考文献
[
62
]
[62]
[62]:提出一个基于策略网络(policy networks)的强化学习算法指导微调。
- 参考文献
-
微调的两种方法:
-
领域适应调优(domain adaptive tuning):参考文献
[
74
,
63
,
32
]
[74,63,32]
[74,63,32]指在源领域预训练模型,然后在目标领域的训练样本对上进行调优,通常预训练任务是无监督的,如Figure 13所示,参考文献
[
74
,
63
]
[74,63]
[74,63]提出在微调时首先会先在一个与预训练任务相关的适应性任务
T
′
\mathcal T'
T′上进行微调,然后再在目标领域
T
\mathcal T
T上进行微调,两阶段的微调常可以通过多任务学习(multi-task learning)技术进行结合。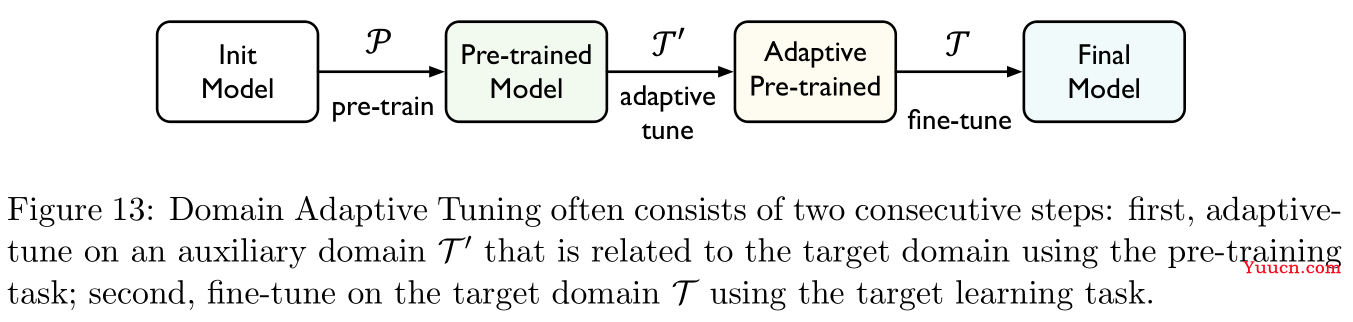
-
正则化调优(regularization tuning):参考文献
[
86
,
101
,
103
,
202
,
79
]
[86,101,103,202,79]
[86,101,103,202,79]
min
θ
∑
i
=
1
m
L
(
h
θ
(
x
i
)
,
y
i
)
+
λ
⋅
Ω
(
θ
)
(9)
\min_{\theta}\sum_{i=1}^mL(h_{\theta}({\bf x}_i),{\bf y}_i)+\lambda\cdot\Omega(\theta)\tag{9}
θmini=1∑mL(hθ(xi),yi)+λ⋅Ω(θ)(9)
其中
L
L
L是损失函数,
Ω
\Omega
Ω是正则项的一般形式(如
Ω
(
θ
)
=
∥
θ
∥
2
2
/
2
\Omega(\theta)=\|\theta\|_2^2/2
Ω(θ)=∥θ∥22/2即为
L
2
L_2
L2正则项),
λ
\lambda
λ是惩罚系数。这里记录参考文献
[
86
]
[86]
[86]提出的弹性权重合并(Elastic Weight Consolidation,EWC)中使用的正则项:
Ω
(
θ
)
=
∑
j
1
2
F
j
∥
θ
j
−
θ
j
∥
2
2
(10)
\Omega(\theta)=\sum_j\frac12F_j\|\theta_j-\theta_j^0\|_2^2\tag{10}
Ω(θ)=j∑21Fj∥θj−θj0∥22(10)
其中
F
F
F是费雪信息矩阵估计量(estimated Fisher information matrix),
θ
j
\theta_j
θj与
θ
j
\theta_j^0
θj0分别是微调后的模型与预训练模型对应网络层的参数,正则项本质是希望微调不会太多改变预训练模型的网络层权重。事实上,EWC基于的假设是如果网络层的权重相似,那么它们的输出也是相似的,但是因为神经网络的尺寸越来越大,网络层权重的微小改变极容易产生蝴蝶效应,因此海域另外两篇参考文献
[
101
,
103
]
[101,103]
[101,103]提出的DELTA与LWF,前者正则化的是预训练模型与微调模型对应网络层输出特征之间差值,后者正则化的是直接是模型最终输出结果差值,三者具体图示详见Figure 14: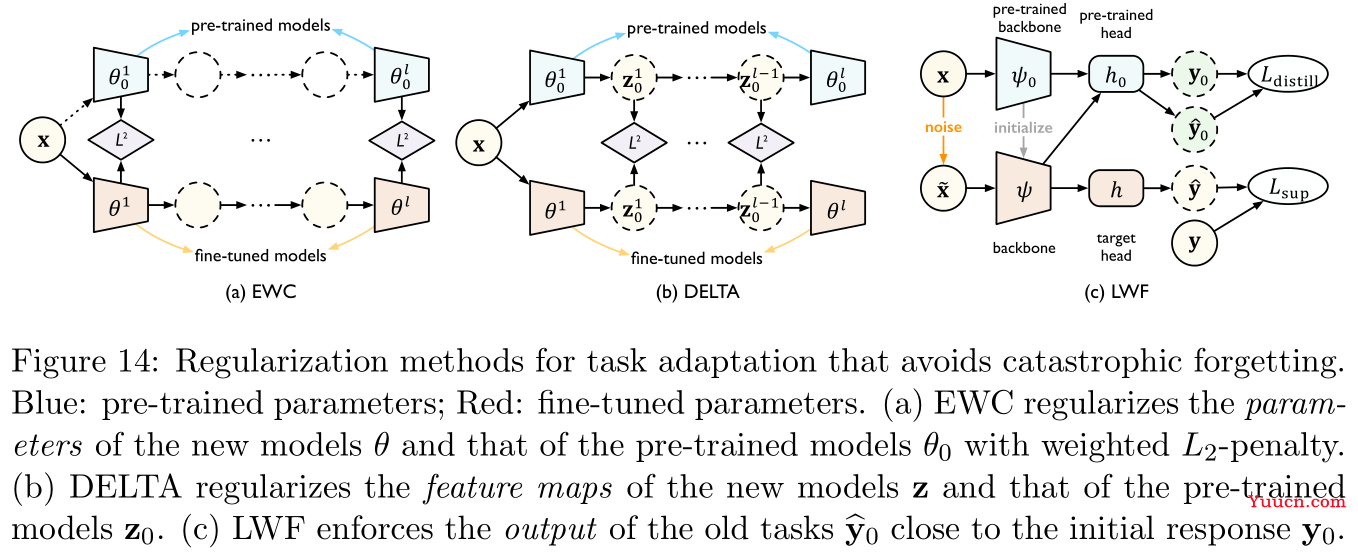
另一种正则化的思想基于正则化本质是使得模型更加平滑,因此参考文献
[
202
,
79
]
[202,79]
[202,79]直接通过使得在对模型输入进行微小扰动的情况下,模型输出不能发生太大变化,以强制实现平滑模型,如此构建的正则项为:
Ω
(
θ
)
=
∑
i
=
1
m
max
∥
x
~
i
−
x
∥
p
≤
ϵ
L
s
(
h
θ
(
x
~
i
)
,
h
θ
(
x
i
)
)
(11)
\Omega(\theta)=\sum_{i=1}^m\max_{\|\tilde {\bf x}_i-{\bf x}\|_p\le\epsilon}L_s(h_{\theta}(\tilde {\bf x}_i),h_{\theta}({\bf x}_i))\tag{11}
Ω(θ)=i=1∑m∥x~i−x∥p≤ϵmaxLs(hθ(x~i),hθ(xi))(11)
其中
ϵ
>
\epsilon>0
ϵ>0是一个小正数,
x
i
{\bf x}_i
xi与
x
~
i
\tilde{\bf x}_i
x~i是扰动前后的模型输入,
L
s
L_s
Ls是衡量两个模型输出的距离的损失函数,比如用于分类的对称KL散度或者均方误差。最后一种其他的正则化方法是基于参数更新策略:
- 参考文献
[
89
]
[89]
[89]:随机标准化(stochastic normalization),即随机用预训练模型中的批正则化层(batch-normalization layer,参考文献
[
77
]
[77]
[77])的统计量(statistics)来替换掉目标统计量,由此作为一种间接的正则化以减轻对目标统计量的依赖。 - 参考文献
[
96
]
[96]
[96]:直接用部分预训练模型权重替换微调模型权重。 - 参考文献
[
193
]
[193]
[193]:根据某种标准只选取部分参数在微调中进行更新。
- 参考文献
-
3.1.2 负迁移 Negative Transfer
-
负迁移(negative transfer)的概念由参考文献
[
142
]
[142]
[142]提出。 -
参考文献
[
187
]
[187]
[187]进一步提出衡量不同领域之间负迁移程度的方法,本文将这种想法推广到预训练与微调。
定义
2
2
2(负迁移差距):
h
θ
(
U
,
T
)
h_{\theta}(\mathcal{U,T})
hθ(U,T)表示从上游数据
U
\mathcal U
U中预训练的模型适应到目标数据
T
\mathcal T
T中的一个模型,
h
θ
(
∅
,
T
)
h_{\theta}(\emptyset,\mathcal T)
hθ(∅,T)表示直接从
T
\mathcal T
T上训练得到的模型,则负迁移差距(negative transfer gap)定义为:
NTG
=
ϵ
T
(
h
θ
(
U
,
T
)
)
−
ϵ
T
(
h
θ
(
∅
,
T
)
)
(12)
\text{NTG}=\epsilon_{\mathcal T}(h_{\theta}(\mathcal{U,T}))-\epsilon_{\mathcal T}(h_{\theta}(\emptyset,\mathcal{T}))\tag{12}
NTG=ϵT(hθ(U,T))−ϵT(hθ(∅,T))(12)
称发生了负迁移,若
NTG
\text{NTG}
NTG为正。
笔者注:
根据定义,
NTG
\text{NTG}
NTG衡量的是迁移得到的模型与直接训练得到的模型之间的性能差距(损失函数值之间的差距)。若
NTG
\text{NTG}
NTG为正,即发生了负迁移,这说明迁移得到的模型还不如直接从目标数据上进行训练得到的模型,那么迁移本身就是无意义的。
-
负迁移出现的原因:
-
上游任务与下游任务关联度不高的情形(分布漂移过大):参考文献
[
109
,
207
]
[109,207]
[109,207]是分词预测和文档分类中的情形; -
取决于已标注的目标数据规模:并不是越大越好,参考文献
[
187
,
66
]
[187,66]
[187,66]就说明ImageNet预训练模型在进行大规模实体发现数据集上(比如COCO数据集)的表现就不是很理想; -
取决于任务适应性算法:理想的适应性算法应当能够提升相关任务之间的正迁移性而避免不相关任务之间的负迁移性,但是这两者其实是矛盾的,具体如Figure 15所示:
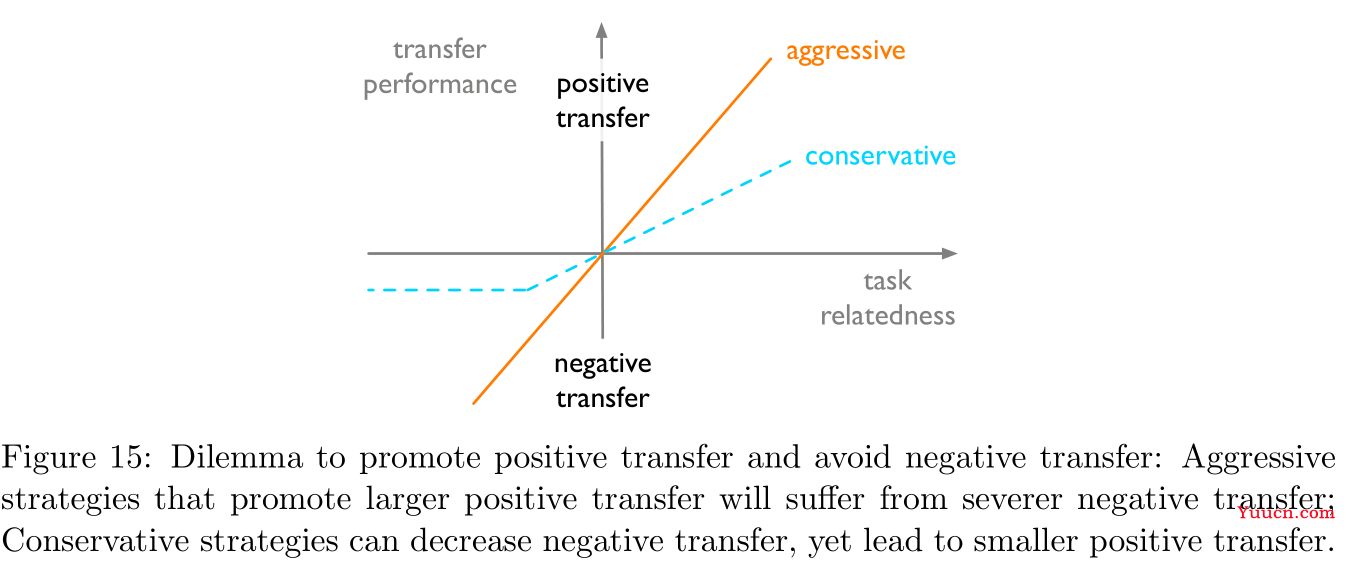
-
-
避免负迁移的方法:(这部分感觉废话居多,纯凑字数)
-
增强安全迁移(enhancing safe transfer):参考文献
[
27
,
78
,
160
,
186
]
[27,78,160,186]
[27,78,160,186],指识别出预训练模型中具有危害的知识。 -
选取正确的预训练模型:参考文献
[
199
,
123
,
198
,
68
,
23
]
[199,123,198,68,23]
[199,123,198,68,23]
-
增强安全迁移(enhancing safe transfer):参考文献
3.1.3 参数功效 Parameter Efficiency
-
参数功效(parameter efficiency)考察的是预训练模型会为每一个下游任务生成完整的一套模型参数,这在存储上非常不利。一种解决方案是使用参考文献
[
20
]
[20]
[20]提出的多任务学习技术,即微调一个模型来解决多个目标任务,或许对每一个目标任务都有利。问题在于多个目标任务未必关联度很高,此时还是需要分别微调,且多任务学习需要同时访问每一个目标任务,这在线上场景(online scenarios)中是不可实现的(目标任务是一个接一个到来的)。 -
提升参数功效的方法:
-
残差调优(residual tuning):参考文献
[
64
,
203
,
73
,
139
,
183
]
[64,203,73,139,183]
[64,203,73,139,183]残差调优的思想源于拟合残差要比直接拟合函数更容易。这里只记录参考文献
[
64
]
[64]
[64]的方法(其他几篇写得都太笼统,没有什么参考意义),固定预训练模型
h
p
r
e
t
r
a
i
n
e
d
h_{\rm pretrained}
hpretrained权重,额外训练一个新的模型
h
s
i
d
e
h_{\rm side}
hside来拟合残差,最终的模型为
h
(
x
)
=
α
h
p
r
e
t
r
a
i
n
e
d
+
(
1
−
α
)
h
s
i
d
e
h(x)=\alpha h_{\rm pretrained}+(1-\alpha)h_{\rm side}
h(x)=αhpretrained+(1−α)hside,注意
α
\alpha
α在训练过程中是可以发生改变的。 -
参数差异调优(parameter difference tuning):参考文献
[
62
,
103
,
119
]
[62,103,119]
[62,103,119]
θ
t
a
s
k
=
θ
p
r
e
t
r
a
i
n
e
d
⊕
δ
t
a
s
k
(13)
\theta_{\rm task}=\theta_{\rm pretrained}\oplus\delta_{\rm task}\tag{13}
θtask=θpretrained⊕δtask(13)
其中
⊕
\oplus
⊕是元素级别相加(其实跟普通加法也没啥区别),
θ
p
r
e
t
r
a
i
n
e
d
\theta_{\rm pretrained}
θpretrained是固定的预训练模型权重,
δ
t
a
s
k
\delta_{\rm task}
δtask则是具体任务不同的残差权重,我们的目的是归约(reduce)
δ
t
a
s
k
\delta_{\rm task}
δtask以实现参数功效。- 参考文献
[
62
]
[62]
[62]:使用
L
L_0
L0的惩罚项(参考文献
[
117
]
[117]
[117]),以使得
δ
t
a
s
k
\delta_{\rm task}
δtask稀疏。 - 参考文献
[
103
]
[103]
[103]:使用参考文献
[
2
]
[2]
[2]提出的FastFood变换矩阵
M
M
M以使得
δ
t
a
s
k
\delta_{\rm task}
δtask低维(
δ
t
a
s
k
=
δ
l
o
w
M
\delta_{\rm task}=\delta_{\rm low}M
δtask=δlowM)。 - 参考文献
[
119
]
[119]
[119]:将加法替换为乘法,即
θ
t
a
s
k
=
θ
p
r
e
t
r
a
i
n
e
d
⊙
δ
t
a
s
k
\theta_{\rm task}=\theta_{\rm pretrained}\odot\delta_{\rm task}
θtask=θpretrained⊙δtask
- 参考文献
两种方法的区别在于前者认为可迁移性源于模型输出特征,后者认为可迁移性源于模型权重。
-
3.1.4 数据功效 Data Efficiency
-
数据功效(data efficiency)讨论的是适应训练需要耗费大量标注样本对,为降低对训练数据的依赖性,由此引出的概念是少射学习(few-shot learning)与零射学习(zero-shot learning)。主要的思路有两个,一是提升预训练模型的广泛适用性(可以集成更多的知识和数据到预训练模型中),二是根据源领域数据简单快捷地生成目标领域数据及其标注。
-
提升数据功效的方法:,
-
指标学习(metric learning):参考文献
[
180
,
162
,
24
]
[180,162,24]
[180,162,24]主要指的是大模型在少量数据训练极易过拟合,但是可以考虑使用一些非参方法,比如近邻算法可以有效处理过拟合、少射问题、零射问题等。
- 参考文献
[
180
]
[180]
[180]:注意力机制在获得加权近邻方面的应用。(感觉这也太牵强了) - 参考文献
[
162
]
[162]
[162]:对于分类问题,认为每一类中所有样本特征的均值可以作为该类别的类型(prototype),然后通过寻找每个样本最近的类型来进行分类。(其实就是标准的聚类算法) - 参考文献
[
24
]
[24]
[24]:将线性分类器替换为基于余弦距离的分类器,用于少射学习。
- 参考文献
-
提示学习(prompt learning):
-
笔者注:
起初感觉有点像软件工程里的敏捷开发,而翻译成敏捷学习,但是似乎跟提示更关联。
以参考文献
[
18
]
[18]
[18]中的超大预训练模型GPT-3为例,在微调过程中,模型接受输入
x
\bf x
x并预测输出
y
\bf y
y的概率为
P
(
y
∣
x
)
P({\bf y}|{\bf x})
P(y∣x),而在提示过程中,根据提示模板(prompt template)将原始输入
x
\bf x
x挖去一些槽位(unfilled slots)得到
x
~
{\bf \tilde x}
x~,预训练模型将会将
x
~
{\bf \tilde x}
x~中挖去的槽位补上得到
x
^
\bf \hat x
x,并得到基于
x
^
\bf \hat x
x的输出
y
\bf y
y,具体操作如下表所示:名称 标记 例子 输入
x
\bf x
x我喜欢这部电影 输出
y
\bf y
y情感极性:正 提示模板
f
p
r
o
m
p
t
(
x
)
f_{\rm prompt}({\bf x})
fprompt(x)
[
X
]
[X]
[X]总之这是一部
[
Z
]
[Z]
[Z]电影提示输入(未填充)
x
~
\bf \tilde x
x~我喜欢这部电影,总之这是一部
[
Z
]
[Z]
[Z]电影提示输入(已填充)
x
^
\bf \hat x
x我喜欢这部电影,总之这是一部好电影 引入提示的好处是可以处理少射任务或零射任务的适应学习,尤其在问答系统中有用。
最后是将提示学习与微调相结合的方法:参考文献
[
151
,
100
,
189
]
[151,100,189]
[151,100,189],具体如Figure 17所示: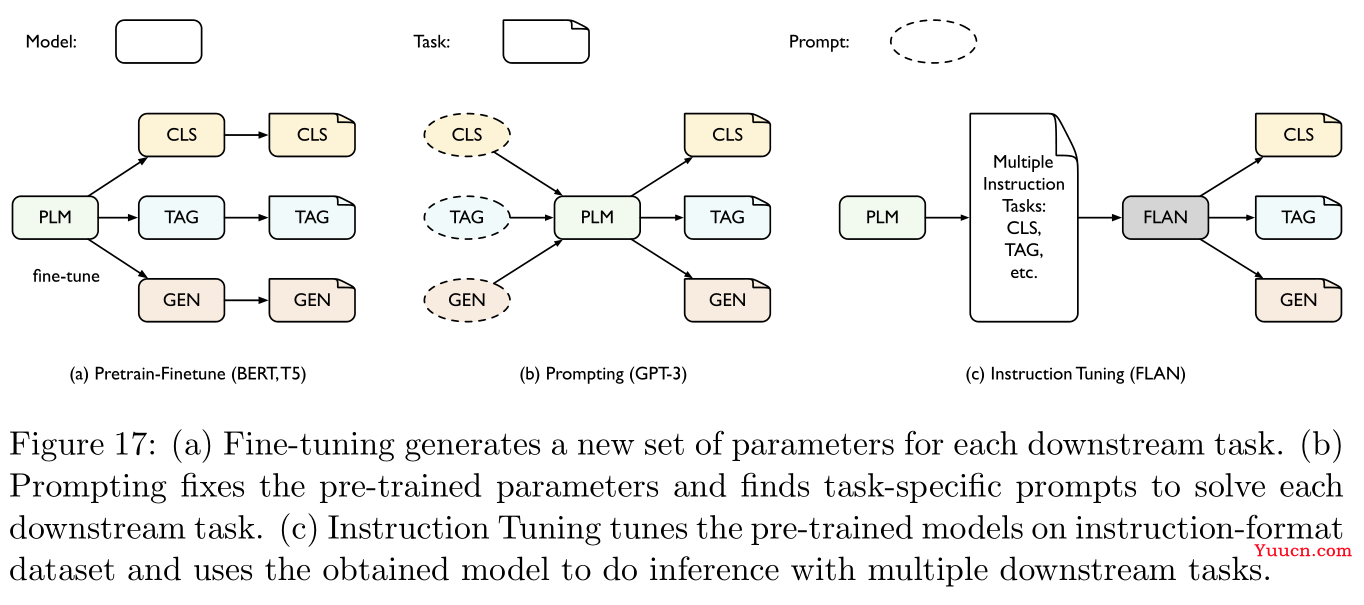
-
-
3.1.5 注释 Remarks
总结一下本小节所有方法的性能:
| 方法 | 适应性能 | 数据功效 | 参数功效 | 模态延展性 | 任务延展性 |
|---|---|---|---|---|---|
| 特征转换 | 差 | 中 | 优 | 优 | 优 |
| 平凡微调 | 优 | 差 | 差 | 优 | 优 |
| 领域适应性调优 | 优 | 中 | 差 | 中 | 优 |
| 正则化调优 | 优 | 中 | 差 | 优 | 差 |
| 残差调优 | 中 | 中 | 中 | 中 | 中 |
| 参数差异调优 | 中 | 中 | 中 | 优 | 优 |
| 指标学习 | 差 | 优 | 优 | 优 | 差 |
| 提示学习 | 中 | 优 | 优 | 差 | 差 |
字段说明:
- 适应性能(adaptation performance):下游任务中有大量标注数据时的模型性能。
- 数据功效(data efficiency):下游任务中只有少量数据时的模型性能。
- 参数功效(parameter efficiency):在下游任务数量不断增加时,能否控制住参数总量。
- 模态延展性(modality scalability):能否用于多模态数据,如文本、图片、音像。
- 任务延展性(task scalability):能否轻松的将预训练模型迁移到不同下游任务中。
3.2 领域适应性 Domain Adaptation
所谓领域适应性(Domain Adaptation),指的是在目标领域中训练数据是未标注的,源领域中的训练数据是已标注的。因此试图在源领域中预训练模型,再设法迁移到目标领域中进行微调。尽管源领域与目标领域的数据存在某种关联性,但是在分布上必然存在一定差异,因而往往迁移微调的模型性能欠佳。这种现象称为分布漂移(distribution shift,参考文献
[
133
]
[133]
[133]),领域适应性正是用于消除训练领域与测试领域之间的分布漂移问题。
传统的领域适应性方法如重加权(re-weighting)、从源领域采样(参考文献
[
165
]
[165]
[165])、建模源领域分布特征空间到目标领域分布特征空间的转换(参考文献
[
53
]
[53]
[53]]),这些方法相对平凡,如参考文献
[
76
,
126
,
111
]
[76,126,111]
[76,126,111]研究的是核重生希尔伯特空间(kernel-reproducing Hilbert space)分布映射方法,参考文献
[
53
]
[53]
[53]研究的是将主成分轴(principal axes)与各个领域分布相联系。本综述着重探讨的是深度领域适应性(deep domain adaptation),即采用深度学习模型架构来建模适应性模块,用于匹配不同领域的数据分布
在无监督领域适应性(unsupervised domain adaptation,UDA)中,源领域
S
^
=
{
(
x
i
s
,
y
i
s
)
}
i
=
1
n
\mathcal{\hat S}=\{({\bf x}_i^{s},{\bf y}_i^{s})\}_{i=1}^n
S={(xis,yis)}i=1n中包含
n
n
n个已标注的样本,目标领域
T
^
=
{
x
i
t
}
i
=
1
m
\mathcal{\hat T}=\{{\bf x}_i^t\}_{i=1}^m
T={xit}i=1m中包含
m
m
m个未标注的样本,目标是学习算法来找到一种假设(hypothesis,其实就是映射)
h
∈
H
:
X
→
Y
h\in\mathcal{H}:\mathcal{X\rightarrow Y}
h∈H:X→Y,使得目标风险最小化:
minimize
ϵ
T
(
h
)
=
E
(
x
t
,
y
t
)
∼
T
[
l
(
h
(
x
t
)
,
y
t
)
]
\text{minimize}\quad\epsilon_{\mathcal{T}}(h)=\mathbb{E}_{({\bf x}^t,{\bf y}^t)\sim\mathcal{T}}[l(h({\bf x}^t),{\bf y}^t)]
minimizeϵT(h)=E(xt,yt)∼T[l(h(xt),yt)]
其中
l
:
Y
×
Y
→
R
+
l:\mathcal{Y\times Y}\rightarrow\R_+
l:Y×Y→R+是损失函数。目前关于UDA的理论研究核心在于如何通过源风险
ϵ
S
\epsilon_{\mathcal{S}}
ϵS以及分布距离(distribution distance)来控制目标风险
ϵ
T
(
h
)
\epsilon_{\mathcal{T}}(h)
ϵT(h)的量级,这里主要介绍两个经典的研究理论
H
Δ
H
\mathcal{H}\Delta\mathcal{H}
HΔH散度(Divergence,参考文献
[
9
,
10
,
120
]
[9,10,120]
[9,10,120])与差距矛盾(Disparity Discrepancy,参考文献
[
204
]
[204]
[204]),以及如何基于这些理论设计不同的算法。
-
笔者注:
这里的假设
h
h
h可以理解为机器学习的黑盒模型,假设只分真伪,因此
h
h
h的输出应该是只有零一值,即针对的是二分类问题。风险(risk)可以理解为损失函数值(的数学期望),整体来看说的就是在降低模型训练的损失值。
首先使用三角不等式,可以构建目标风险与源风险之间的不等关系:
定理
3
3
3(Bound with Disparity):假设损失函数
l
l
l是对称的(symmetric)且服从三角不等式,定义任意两个在分布
D
\mathcal{D}
D上的假设
h
h
h与
h
′
h'
h′之间差距(disparity):
ϵ
D
(
h
,
h
′
)
=
E
x
,
y
∼
D
[
l
(
h
(
x
)
,
h
′
(
x
)
)
]
(14)
\epsilon_{\mathcal{D}}(h,h')=\mathbb{E}_{{\bf x},{\bf y}\sim\mathcal{D}}[l(h({\bf x}),h'({\bf x}))]\tag{14}
ϵD(h,h′)=Ex,y∼D[l(h(x),h′(x))](14)
则目标风险
ϵ
T
(
h
)
\epsilon_{\mathcal{T}}(h)
ϵT(h)满足:
ϵ
T
(
h
)
≤
ϵ
S
(
h
)
+
[
ϵ
S
(
h
∗
)
+
ϵ
T
(
h
∗
)
]
+
∣
ϵ
S
(
h
,
h
∗
)
−
ϵ
T
(
h
,
h
∗
)
∣
(15)
\epsilon_{\mathcal{T}}(h)\le\epsilon_{\mathcal{S}}(h)+[\epsilon_{\mathcal{S}}(h^*)+\epsilon_{\mathcal{T}}(h^*)]+|\epsilon_{\mathcal{S}}(h,h^*)-\epsilon_{\mathcal{T}}(h,h^*)|\tag{15}
ϵT(h)≤ϵS(h)+[ϵS(h∗)+ϵT(h∗)]+∣ϵS(h,h∗)−ϵT(h,h∗)∣(15)
其中
h
∗
=
argmax
h
∈
H
[
ϵ
S
(
h
)
+
ϵ
T
(
h
)
]
h^*=\text{argmax}_{h\in\mathcal{H}}[\epsilon_{\mathcal{S}}(h)+\epsilon_{\mathcal{T}}(h)]
h∗=argmaxh∈H[ϵS(h)+ϵT(h)]是理想联合假设(ideal joint hypothesis),
ϵ
ideal
=
ϵ
S
(
h
∗
)
+
ϵ
T
(
h
∗
)
\epsilon_{\text{ideal}}=\epsilon_{\mathcal{S}}(h^*)+\epsilon_{\mathcal{T}}(h^*)
ϵideal=ϵS(h∗)+ϵT(h∗)是理想联合误差(ideal joint error),
∣
ϵ
S
(
h
,
h
∗
)
−
ϵ
T
(
h
,
h
∗
)
∣
|\epsilon_{\mathcal{S}}(h,h^*)-\epsilon_{\mathcal{T}}(h,h^*)|
∣ϵS(h,h∗)−ϵT(h,h∗)∣是分布
S
\mathcal{S}
S与
T
\mathcal T
T之间的差距差异(disparity difference)。
笔者注:
损失函数对称即满足交换律,即
l
(
y
1
,
y
2
)
=
l
(
y
2
,
y
1
)
l(y_1,y_2)=l(y_2,y_1)
l(y1,y2)=l(y2,y1);损失函数可以看作是两个向量之间的差异,因此式
(
14
)
(14)
(14)衡量的是两个假设(即模型)预测结果的差异程度。
在领域适应性的研究中,通常假定理想联合误差(即源领域任务与目标领域任务的损失函数之和)是充分小的,否则领域适应本身就是不可行的(即无法训练至损失函数达到低水平,对应参考文献
[
10
]
[10]
[10]中提出的不可能定理,impossibility theorem),此时式
(
15
)
(15)
(15)中只需要考察最后一项差距差异的数值。
然而目标数据集标签不可得,于是理想假设
h
∗
h^*
h∗是未知的,因此差距差异并不能直接估计,
H
Δ
H
\mathcal{H}\Delta\mathcal{H}
HΔH散度正是用于衡量差距差异的上界:
定义
4
4
4(
H
Δ
H
\mathcal{H}\Delta\mathcal{H}
HΔH散度):定义
H
Δ
H
=
Δ
{
h
∣
h
=
h
1
⊗
h
2
,
h
1
,
h
2
∈
H
}
\mathcal{H}\Delta\mathcal{H}\overset{\Delta}{=}\{h|h=h_1\otimes h_2,h_1,h_2\in\mathcal{H}\}
HΔH=Δ{h∣h=h1⊗h2,h1,h2∈H}为假设空间
H
\mathcal{H}
H的对称差异假设空间(symmetric difference hypothesis space),其中
⊗
\otimes
⊗表示异或运算符(XOR),则分布
S
\mathcal S
S与
T
\mathcal T
T之间的
H
Δ
H
\mathcal{H}\Delta\mathcal{H}
HΔH散度可以表示为:
d
H
Δ
H
(
S
,
T
)
=
Δ
sup
h
,
h
′
∈
H
∣
ϵ
S
(
h
,
h
′
)
−
ϵ
T
(
h
,
h
′
)
∣
d_{\mathcal{H}\Delta\mathcal{H}}(\mathcal{S,T})\overset\Delta=\sup_{h,h'\in\mathcal{H}}|\epsilon_{\mathcal S}(h,h')-\epsilon_{\mathcal T}(h,h')|
dHΔH(S,T)=Δh,h′∈Hsup∣ϵS(h,h′)−ϵT(h,h′)∣
特别地,对于二分类问题的零一损失函数,即
l
(
y
,
y
′
)
=
1
(
y
≠
y
′
)
l(y,y')=\textbf{1}(y\neq y')
l(y,y′)=1(y=y′),有:
d
H
Δ
H
(
S
,
T
)
=
Δ
sup
δ
∈
H
Δ
H
∣
E
S
[
δ
(
x
)
≠
]
−
E
T
[
δ
(
x
)
≠
]
∣
d_{\mathcal{H}\Delta\mathcal{H}}(\mathcal{S,T})\overset\Delta=\sup_{\delta\in\mathcal{H\Delta H}}|\mathbb{E}_{\mathcal{S}}[\delta({\bf x})\neq0]-\mathbb{E}_{\mathcal{T}}[\delta({\bf x})\neq0]|
dHΔH(S,T)=Δδ∈HΔHsup∣ES[δ(x)=0]−ET[δ(x)=0]∣
笔者注:
H
Δ
H
\mathcal{H}\Delta\mathcal{H}
HΔH检验的是两个假设真伪相异的情形(异或运算)。因此第二个式子中
δ
(
x
)
\delta({\bf x})
δ(x)的取值只有零一,
δ
(
x
)
≠
\delta(x)\neq 0
δ(x)=0表示两个假设相异(即模型预测结果不同),整体就是两个假设差异之间的绝对值(即距离)。然后再重新看第一个式子,根据式
(
14
)
(14)
(14)可知,
ϵ
D
(
h
,
h
′
)
\epsilon_{\mathcal{D}}(h,h')
ϵD(h,h′)衡量的是两个假设(即模型)
h
h
h与
h
′
h'
h′在分布
D
\mathcal{D}
D上预测结果的差异值,而绝对值衡量的是距离,因此合起来就是差距的差距,简称差距差异。
可以通过有限数量采样自源领域与目标领域的未标注样本来对
H
Δ
H
\mathcal{H}\Delta\mathcal{H}
HΔH散度进行估计(即使用多组不同的模型对分别在源领域与目标领域上预测结果并计算差距差异),但是具体计算优化非常困难的。通常的做法是训练一个领域辨识器(domain discriminator)
D
D
D来划分源领域与目标领域的样本(参考文献
[
9
,
45
]
[9,45]
[9,45])。我们假定辨识器族(family of the discriminators)丰富到足以包含
H
Δ
H
\mathcal{H\Delta H}
HΔH,即
H
Δ
H
⊂
H
D
\mathcal{H\Delta H}\subset\mathcal{H}_D
HΔH⊂HD(比如神经网络可用于近似几乎所有的函数),则
H
Δ
H
\mathcal{H}\Delta\mathcal{H}
HΔH散度可以进一步控制在下式的范围内:
sup
D
∈
H
D
∣
E
S
[
D
(
x
)
=
1
]
+
E
T
[
D
(
x
)
=
]
∣
\sup_{D\in \mathcal{H}_D}|\mathbb E_{\mathcal S}[D({\bf x})=1]+\mathbb{E}_{\mathcal T}[D({\bf x})=0]|
D∈HDsup∣ES[D(x)=1]+ET[D(x)=0]∣
-
笔者注:
D
(
x
)
=
D({\bf x})=0
D(x)=0表示样本
x
\bf x
x属于源领域,
D
(
x
)
=
1
D({\bf x})=1
D(x)=1表示样本
x
\bf x
x属于目标领域,因此绝对值中的两项都表示预测结果错误的概率,但是根据差距差异的定义,是否应当是减号而非加号?
这种思想衍生出Section 3.2.2中领域对立(domain adversarial)方法。此外,若使用非参数方法对
H
Δ
H
\mathcal{H}\Delta\mathcal{H}
HΔH散度进行估计,比如将
H
Δ
H
\mathcal{H}\Delta\mathcal{H}
HΔH用某个函数空间
F
\mathcal F
F替代,即衍生出Section 3.2.1中的统计匹配(statistics matching)方法。
-
笔者注:
根据定义,
H
Δ
H
\mathcal{H}\Delta\mathcal{H}
HΔH本身也是一个假设空间,可以理解为是一个模型集合或者映射组,因此是可以用某个函数族对它进行近似。
下面这个定理是关于领域适应性最早的研究之一,它简历了基于
H
Δ
H
\mathcal{H}\Delta\mathcal{H}
HΔH散度的二分类问题的一般上界:
定理
5
5
5(参考文献
[
10
]
[10]
[10]):
H
\mathcal{H}
H是一个二进制假设空间(binary hypothesis space),若
S
^
\mathcal{\hat S}
S与
T
^
\mathcal{\hat T}
T都是容量为
m
m
m的样本,则对于任意
δ
∈
(
,
1
)
\delta\in(0,1)
δ∈(0,1),至少有
1
−
δ
1-\delta
1−δ概率下式成立:
ϵ
T
(
h
)
≤
ϵ
S
(
h
)
+
d
H
Δ
H
(
S
^
,
T
^
)
+
ϵ
i
d
e
a
l
+
4
2
d
log
(
2
m
)
+
log
(
2
/
δ
)
m
(
∀
h
∈
H
)
(16)
\epsilon_{\mathcal{T}}(h)\le\epsilon_{\mathcal{S}}(h)+d_{\mathcal{H}\Delta\mathcal{H}}(\mathcal{\hat S,\hat T})+\epsilon_{\rm ideal}+4\sqrt{\frac{2d\log(2m)+\log(2/\delta)}{m}}\quad(\forall h\in\mathcal H)\tag{16}
ϵT(h)≤ϵS(h)+dHΔH(S,T)+ϵideal+4m2dlog(2m)+log(2/δ)(∀h∈H)(16)
**定理
5
5
5**的缺陷在于只能用于二分类问题,因此参考文献
[
45
]
[45]
[45]将它推广到了多分类的情形:
定理
6
6
6(参考文献
[
45
]
[45]
[45]):假设损失函数
l
l
l对称且服从三角不等式,定义
h
S
∗
=
argmin
h
∈
H
ϵ
S
(
h
)
h
T
∗
=
argmin
h
∈
H
ϵ
T
(
h
)
h_{\mathcal S}^*=\text{argmin}_{h\in\mathcal{H}}\epsilon_{\mathcal{S}}(h)\\ h_{\mathcal T}^*=\text{argmin}_{h\in\mathcal{H}}\epsilon_{\mathcal{T}}(h)
hS∗=argminh∈HϵS(h)hT∗=argminh∈HϵT(h)
分别表示源领域与目标领域的理想假设,则有:
ϵ
T
(
h
)
≤
ϵ
S
(
h
,
h
S
∗
)
+
d
H
Δ
H
(
S
,
T
)
+
ϵ
(
∀
h
∈
H
)
(17)
\epsilon_{\mathcal{T}}(h)\le\epsilon_{\mathcal{S}}(h,h^*_{\mathcal S})+d_{\mathcal{H}\Delta\mathcal{H}}(\mathcal{S,T})+\epsilon\quad(\forall h\in\mathcal{H})\tag{17}
ϵT(h)≤ϵS(h,hS∗)+dHΔH(S,T)+ϵ(∀h∈H)(17)
其中
ϵ
S
(
h
,
h
S
∗
)
\epsilon_{\mathcal{S}}(h,h^*_{\mathcal S})
ϵS(h,hS∗)表示源领域风险,
ϵ
\epsilon
ϵ表示适应能力:
ϵ
=
ϵ
T
(
h
T
∗
)
+
ϵ
S
(
h
T
∗
,
h
S
∗
)
\epsilon=\epsilon_{\mathcal T}(h_{\mathcal T}^*)+\epsilon_{\mathcal S}(h_{\mathcal T}^*,h_{\mathcal S}^*)
ϵ=ϵT(hT∗)+ϵS(hT∗,hS∗)
进一步,若
l
l
l有界,即
∀
(
y
,
y
′
)
∈
Y
2
,
∃
M
>
\forall (y,y')\in\mathcal{Y}^2,\exists M>0
∀(y,y′)∈Y2,∃M>0,使得
l
(
y
,
y
′
)
≤
M
l(y,y')\le M
l(y,y′)≤M。如定义
l
(
y
,
y
′
)
=
∣
y
−
y
′
∣
q
l(y,y')=|y-y'|^q
l(y,y′)=∣y−y′∣q,若
S
^
\mathcal{\hat S}
S与
T
^
\mathcal{\hat T}
T是容量为
n
n
n和
m
m
m的样本,则至少有
1
−
δ
1-\delta
1−δ的概率下式成立:
d
H
Δ
H
(
S
,
T
)
≤
d
H
Δ
H
(
S
^
,
T
^
)
+
4
q
(
R
n
,
S
(
H
)
+
R
m
,
T
(
H
)
)
+
3
M
(
log
(
4
/
δ
)
2
n
+
log
(
4
/
δ
)
2
m
)
(18)
d_{\mathcal{H}\Delta\mathcal{H}}(\mathcal{S,T})\le d_{\mathcal{H}\Delta\mathcal{H}}(\mathcal{\hat S,\hat T})+4q(\mathfrak{R}_{n,\mathcal{S}}(\mathcal{H})+\mathfrak{R}_{m,\mathcal{T}}(\mathcal{H}))+3M\left(\sqrt{\frac{\log(4/\delta)}{2n}}+\sqrt{\frac{\log(4/\delta)}{2m}}\right)\tag{18}
dHΔH(S,T)≤dHΔH(S,T)+4q(Rn,S(H)+Rm,T(H))+3M(2nlog(4/δ)+2mlog(4/δ))(18)
其中
R
n
,
D
\mathfrak{R}_{n,\mathcal{D}}
Rn,D表示期望拉德马赫复杂度(Expected Rademacher Complexity,参考文献
[
6
]
[6]
[6])。
上述所有的
H
Δ
H
\mathcal{H}\Delta\mathcal{H}
HΔH散度的上界依然太松弛(因为
h
h
h和
h
′
h'
h′是可以任取的,那么取上确界值就会非常大),因此参考文献
[
204
]
[204]
[204]考虑固定其中一个假设,提出差距矛盾的概念(请与上面的差距差异进行区分,一个是disparity discrepancy,一个是disparity difference):
定义
7
7
7(差距矛盾):给定二进制假设空间
H
\mathcal{H}
H以及一个具体的假设
h
∈
H
h\in\mathcal{H}
h∈H,由
h
h
h导出的差距矛盾定义为:
d
h
,
H
(
S
,
T
)
=
sup
h
′
∈
H
(
E
T
1
[
h
′
≠
h
]
−
E
S
1
[
h
′
≠
h
]
)
(19)
d_{h,\mathcal{H}}(\mathcal{S,T})=\sup_{h'\in\mathcal{H}}(\mathbb{E}_{\mathcal T}\textbf{1}[h'\neq h]-\mathbb{E}_{\mathcal S}\textbf{1}[h'\neq h])\tag{19}
dh,H(S,T)=h′∈Hsup(ET1[h′=h]−ES1[h′=h])(19)
笔者注:
对比**定义
4
4
4**中的
H
Δ
H
\mathcal{H}\Delta\mathcal{H}
HΔH散度,这里其实就是固定了一个
h
h
h,别的也没有什么区别。从这边往下的定义和定理基本不具有实用意义。
此时上确界只在一个假设
h
′
h'
h′上任取,因而大大缩小了上界范围,且计算上也要更加容易。差距矛盾可以很好的用来衡量分布漂移(distribution shift)的程度。
定理
8
8
8(参考文献
[
204
]
[204]
[204]):
S
^
\mathcal{\hat S}
S与
T
^
\mathcal{\hat T}
T是容量为
n
n
n和
m
m
m的样本,对于任意的
δ
>
\delta>0
δ>0以及每一个二进制分类器
h
∈
H
h\in\mathcal{H}
h∈H,都有至少
1
−
3
δ
1-3\delta
1−3δ的概率下式成立:
ϵ
T
(
h
)
≤
ϵ
S
^
(
S
^
,
T
^
)
+
d
h
,
H
(
S
^
,
T
^
)
+
ϵ
i
d
e
a
l
+
2
R
n
,
S
(
H
)
+
2
R
n
,
S
(
H
Δ
H
)
+
2
log
(
2
/
δ
)
2
n
+
2
R
m
,
T
(
H
Δ
H
)
+
2
log
(
2
/
δ
)
2
m
(20)
\epsilon_{\mathcal{T}}(h)\le\epsilon_{\mathcal{\hat S}}(\mathcal{\hat S,\hat T})+d_{h,\mathcal H}(\mathcal{\hat S,\hat T})+\epsilon_{\rm ideal}+2\mathfrak{R}_{n,\mathcal S}(\mathcal{H})\\+2\mathfrak{R}_{n,\mathcal S}(\mathcal{H\Delta H})+2\sqrt{\frac{\log(2/\delta)}{2n}}+2\mathfrak{R}_{m,\mathcal T}(\mathcal{H\Delta H})+2\sqrt{\frac{\log(2/\delta)}{2m}}\tag{20}
ϵT(h)≤ϵS(S,T)+dh,H(S,T)+ϵideal+2Rn,S(H)+2Rn,S(HΔH)+22nlog(2/δ)+2Rm,T(HΔH)+22mlog(2/δ)(20)
**定理
8
8
8**是二分类的情形,可以推广到多分类的情形,在此之前我们先给出新的定义:
定义
9
9
9(边际差距矛盾)给定一个得分假设空间(scoring hypothesis space)
F
\mathcal F
F,令
ρ
f
(
x
,
y
)
=
Δ
1
2
(
f
(
x
,
y
)
−
max
y
′
≠
y
f
(
x
,
y
′
)
)
\rho_f(x,y)\overset\Delta=\frac12(f(x,y)-\max_{y'\neq y}f(x,y'))
ρf(x,y)=Δ21(f(x,y)−y′=ymaxf(x,y′))
表示在样本对
(
x
,
y
)
(x,y)
(x,y)处的实假设(real hypothesis)
f
f
f的边际(margin),令
h
f
:
x
→
argmax
y
∈
Y
f
(
x
,
y
)
h_f:x\rightarrow\text{argmax}_{y\in\mathcal Y}f(x,y)
hf:x→argmaxy∈Yf(x,y)
表示由
f
f
f导出的标签函数(labeling function),令
Φ
ρ
(
x
)
=
Δ
{
x
≥
ρ
1
−
x
ρ
≤
x
≤
ρ
1
x
≤
(21)
\Phi_{\rho}(x)\overset\Delta=\left\{\begin{aligned} &0&&x\ge \rho\\ &1-\frac x\rho&&0\le x\le\rho\\ &1&&x\le0\\ \end{aligned}\right.\tag{21}
Φρ(x)=Δ⎩⎪⎪⎨⎪⎪⎧01−ρx1x≥ρ0≤x≤ρx≤0(21)
表示边际损失(margin loss),则在分布
D
\mathcal{D}
D上,
f
f
f与
f
′
f'
f′的边际差距(margin disparity)为:
ϵ
D
(
ρ
)
(
f
′
,
f
)
=
E
(
x
,
y
)
∼
D
[
Φ
ρ
(
ρ
f
′
(
x
,
h
f
(
x
)
)
)
]
(22)
\epsilon_{\mathcal D}^{(\rho)}(f',f)=\mathbb{E}_{(x,y)\sim\mathcal D}[\Phi_{\rho}(\rho_{f'}(x,h_f(x)))]\tag{22}
ϵD(ρ)(f′,f)=E(x,y)∼D[Φρ(ρf′(x,hf(x)))](22)
给定具体的假设
f
∈
F
f\in\mathcal F
f∈F,则边际差距矛盾(margin disparity discrepancy)为:
d
f
,
F
(
ρ
)
(
S
,
T
)
=
sup
f
′
∈
F
[
ϵ
T
(
ρ
)
(
f
′
,
f
)
−
ϵ
S
(
ρ
)
(
f
′
,
f
)
]
(23)
d_{f,\mathcal F}^{(\rho)}(\mathcal{S,T})=\sup_{f'\in\mathcal F}[\epsilon_{\mathcal T}^{(\rho)}(f',f)-\epsilon_{\mathcal S}^{(\rho)}(f',f)]\tag{23}
df,F(ρ)(S,T)=f′∈Fsup[ϵT(ρ)(f′,f)−ϵS(ρ)(f′,f)](23)
根据式
(
22
)
(22)
(22)可知边际差距满足非负性与次可加性(subadditivity),但是并不对称,因此并不能直接将**定理
6
6
6**用到这里来生成一个新的上界,因此我们有本小节最后一个定理:
定理
10
10
10(参考文献
[
204
]
[204]
[204]):在定义
9
9
9的假设条件下,对于任意的
δ
>
\delta>0
δ>0,以及任意的得分函数
f
∈
F
f\in\mathcal F
f∈F,都有至少
1
−
3
δ
1-3\delta
1−3δ的概率下式成立:
ϵ
T
(
h
)
≤
ϵ
S
^
(
ρ
)
(
f
)
+
d
f
,
F
(
ρ
)
(
S
^
,
T
^
)
+
ϵ
i
d
e
a
l
+
2
k
2
ρ
R
n
,
S
(
Π
1
F
)
+
k
ρ
R
n
,
S
(
Π
H
F
)
+
2
log
(
2
/
δ
)
2
n
+
2
R
m
,
T
(
Π
H
F
)
+
2
log
(
2
/
δ
)
2
m
(24)
\epsilon_{\mathcal{T}}(h)\le\epsilon_{\mathcal{\hat S}}^{(\rho)}(f)+d_{f,\mathcal F}^{(\rho)}(\mathcal{\hat S,\hat T})+\epsilon_{\rm ideal}+\frac{2k^2}{\rho}\mathfrak{R}_{n,\mathcal S}(\Pi_1\mathcal{F})\\+\frac k\rho\mathfrak{R}_{n,\mathcal S}(\Pi_{\mathcal H}\mathcal{F})+2\sqrt{\frac{\log(2/\delta)}{2n}}+2\mathfrak{R}_{m,\mathcal T}(\Pi_{\mathcal H}\mathcal{F})+2\sqrt{\frac{\log(2/\delta)}{2m}}\tag{24}
ϵT(h)≤ϵS(ρ)(f)+df,F(ρ)(S,T)+ϵideal+ρ2k2Rn,S(Π1F)+ρkRn,S(ΠHF)+22nlog(2/δ)+2Rm,T(ΠHF)+22mlog(2/δ)(24)
**定理
10
10
10**中的边际上界指出一个恰当的边际
ρ
\rho
ρ可以生成在目标领域上更好的推广结果。定理
8
8
8与定理
10
10
10共同构成Section 3.2.3中的假设对立(hypothesis adversarial)方法。
注意不论是
H
Δ
H
\mathcal{H}\Delta\mathcal{H}
HΔH散度还是差距矛盾,其中的上确界符号
sup
\sup
sup都只在假设空间
H
\mathcal H
H较小的时候才有意义,然而在一般的神经网络模型中,假设空间
H
\mathcal H
H都会非常庞大,此时取上确界就会趋于正无穷而失去意义。但是可以通过在上游任务中进行预训练来缩小假设空间,这就是领域对立与假设对立方法所必要的预训练。
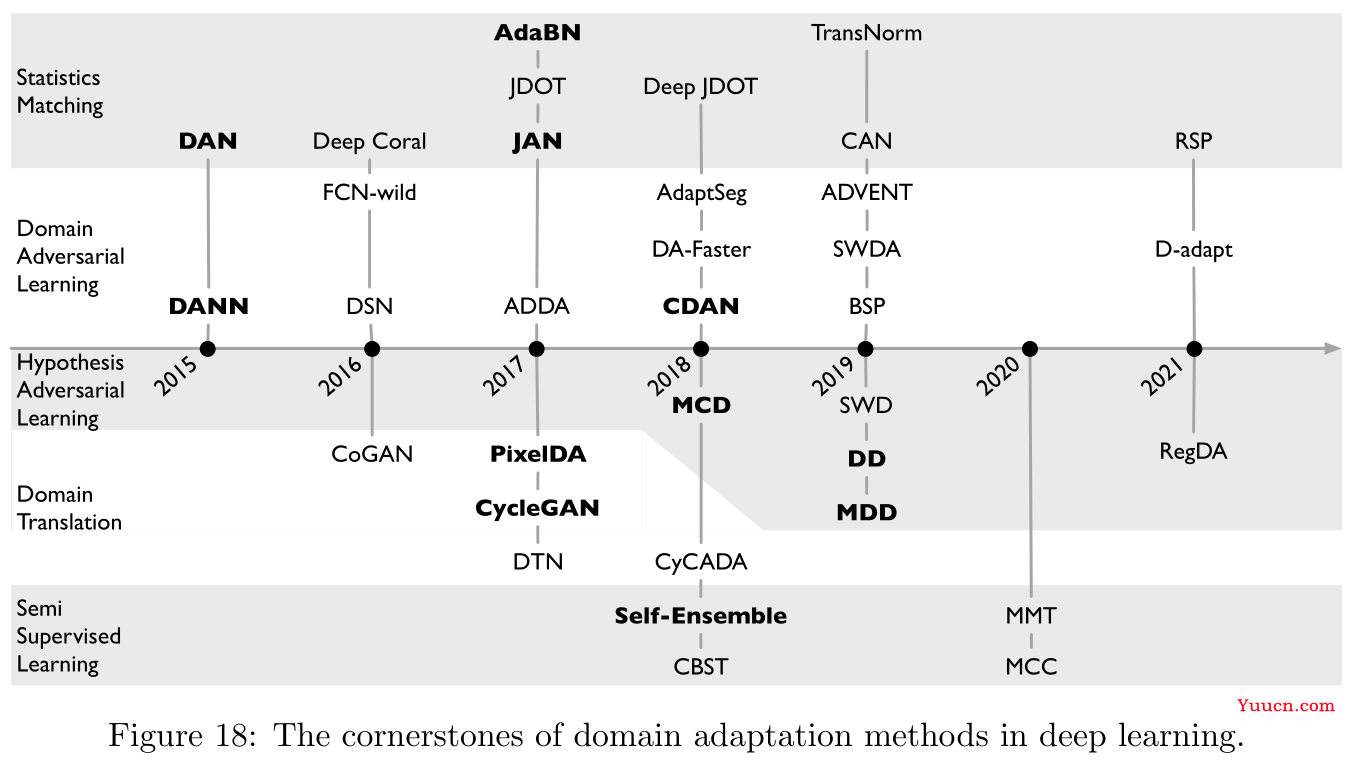
3.2.1 统计匹配 Statistics Matching
上文中已经介绍了很多关于领域适应性的上界理论结果,问题在于这些理论大多依赖假设导出的(hypothesis-induced)分布距离,在没有训练得到模型之前这些理论结果其实都不是很直观,因此本节主要是介绍一些基于统计的概率结果。注意,参考文献
[
112
,
114
]
[112,114]
[112,114]中介绍了非常多基于假设导出的分布距离构建的领域适应性算法。
定义
11
11
11(最大平均差距):给定两个概率分布
S
,
T
\mathcal{S,T}
S,T以及可测空间(measurable space)
X
\bf X
X,整体概率指标(integral probability metric,参考文献
[
140
]
[140]
[140])定义为:
d
F
(
S
,
T
)
=
Δ
sup
f
∈
F
∣
E
x
∼
S
[
f
(
x
)
]
−
E
x
∼
T
[
f
(
x
)
]
∣
d_{\mathcal F}(\mathcal{S,T})\overset\Delta=\sup_{f\in\mathcal F}|\mathbb{E}_{{\bf x}\sim \mathcal{S}}[f({\bf x})]-\mathbb{E}_{{\bf x}\sim \mathcal{T}}[f({\bf x})]|
dF(S,T)=Δf∈Fsup∣Ex∼S[f(x)]−Ex∼T[f(x)]∣
其中
F
\mathcal F
F是
X
\bf X
X上的一类有界函数。参考文献
[
163
]
[163]
[163]进一步将约束
F
\mathcal{F}
F到核希尔伯特空间(kernel Hilbert space,RKHS)
H
k
\mathcal{H}_k
Hk中的一个单位球(unit ball)内,即
F
=
{
f
∈
H
k
:
∥
f
∥
H
k
≤
1
}
\mathcal F=\{f\in\mathcal{H}_k:\|f\|_{\mathcal{H}_k}\le1\}
F={f∈Hk:∥f∥Hk≤1},其中
k
k
k是特征核(characteristic kernel),由此导出最大平均差距(maximum mean discrepancy,MMD,参考文献
[
57
]
[57]
[57]):
d
M
M
D
2
(
S
,
T
)
=
∥
E
x
∈
S
[
ϕ
(
x
)
]
−
E
x
∈
T
[
ϕ
(
x
)
]
∥
H
k
2
(25)
d_{\rm MMD}^2(\mathcal{S,T})=\|\mathbb{E}_{{\bf x}\in\mathcal S}[\phi({\bf x})]-\mathbb{E}_{{\bf x}\in\mathcal T}[\phi({\bf x})]\|_{\mathcal H_k}^2\tag{25}
dMMD2(S,T)=∥Ex∈S[ϕ(x)]−Ex∈T[ϕ(x)]∥Hk2(25)
其中
ϕ
(
x
)
\phi(x)
ϕ(x)是与核函数
k
k
k相关的特征映射,满足:
k
(
x
,
x
′
)
=
<
ϕ
(
x
)
,
ϕ
(
x
′
)
>
k({\bf x},{\bf x}')=\left<\phi({\bf x}),\phi({\bf x}')\right>
k(x,x′)=⟨ϕ(x),ϕ(x′)⟩
可以证明,
S
=
T
\mathcal S=\mathcal T
S=T当前仅当
d
F
(
S
,
T
)
=
d_{\mathcal F}(\mathcal{S,T})=0
dF(S,T)=0或
d
M
M
D
2
(
S
,
T
)
=
d^2_{\rm MMD}(\mathcal{S,T})=0
dMMD2(S,T)=0定理
12
12
12(参考文献
[
140
]
[140]
[140]):给定与定义
11
11
11同样的设定,
l
l
l是一个凸的损失函数,形如
l
(
y
,
y
′
)
=
∣
y
−
y
′
∣
q
l(y,y')=|y-y'|^q
l(y,y′)=∣y−y′∣q,则对于任意
δ
>
\delta>0
δ>0以及
∀
h
∈
F
\forall h\in\mathcal F
∀h∈F,至少有
1
−
δ
1-\delta
1−δ的概率有下式成立:
ϵ
T
(
h
)
≤
ϵ
S
(
h
)
+
d
M
M
D
(
S
^
,
T
^
)
+
ϵ
i
d
e
a
l
+
2
n
E
x
∼
S
[
tr
(
K
S
)
]
+
2
m
E
x
∼
T
[
tr
(
K
T
)
]
+
2
log
(
2
/
δ
)
2
n
+
log
(
2
/
δ
)
2
m
(26)
\epsilon_{\mathcal T}(h)\le\epsilon_{\mathcal S}(h)+d_{\rm MMD}(\mathcal{\hat S,\hat T})+\epsilon_{\rm ideal}+\frac2n\mathbb{E}_{{\bf x}\sim\mathcal S}\left[\sqrt{\text{tr}({\bf K}_{\mathcal{S}})}\right]\\+\frac2m\mathbb{E}_{{\bf x}\sim\mathcal T}\left[\sqrt{\text{tr}({\bf K}_{\mathcal{T}})}\right]+2\sqrt{\frac{\log(2/\delta)}{2n}}+\sqrt{\frac{\log(2/\delta)}{2m}}\tag{26}
ϵT(h)≤ϵS(h)+dMMD(S,T)+ϵideal+n2Ex∼S[tr(KS)]+m2Ex∼T[tr(KT)]+22nlog(2/δ)+2mlog(2/δ)(26)
其中
K
S
{\bf K}_{\mathcal{S}}
KS与
K
T
{\bf K}_{\mathcal{T}}
KT分别表示根据
S
\mathcal{S}
S和
T
\mathcal{T}
T中样本计算得到的核矩阵(kernel matrices)。
其实跟上面的差距差异也没有太大区别,只是重新定义新的距离计算方式,以及把假设换成了函数,但是相较而言有如下的优势:
- 与假设无关的(hypothesis-free),即无需得到确切的模型来衡量分布距离。
- 复杂项(complexity term)与Vapnik-Chervonenkis维度无关。
- MMD的无偏估计量可以在线性时间内计算得到。
- MMD最小化的这个过程在概率论上有一个非常漂亮的统计匹配解释。
与MMD相关的研究有:参考文献
[
174
,
57
,
58
]
[174,57,58]
[174,57,58],比较值得注意的是参考文献
[
57
,
58
]
[57,58]
[57,58]基于深度适应网络(deep adaptation network,DAN,参考文献
[
112
,
116
]
[112,116]
[112,116]),提出MMD的变体多核MMD(multi-kernel MMD,MK-MMD),具体如Figure 19左图所示:
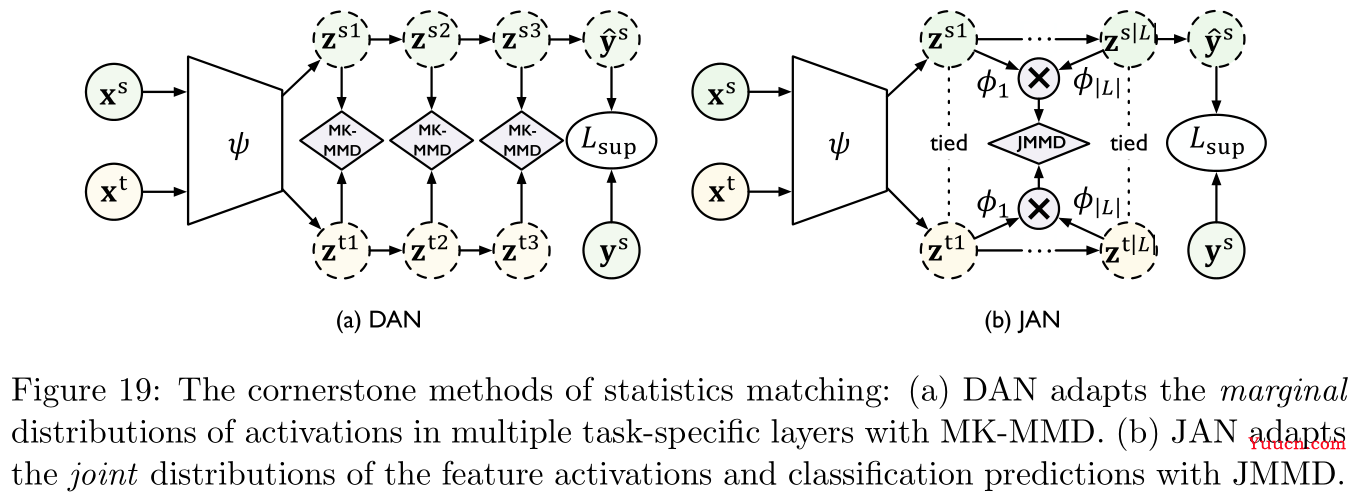
Figure 19中右图是参考文献
[
114
]
[114]
[114]提出的联合适应网络(joint adaptation network,JAN)中的联合最大平均差距(joint maximum mean discrepancy,JMMD),这是用于衡量两个联合分布
P
(
X
s
,
Y
s
)
P({\bf X}^s,{\bf Y}^s)
P(Xs,Ys)与
P
(
X
t
,
Y
t
)
P({\bf X}^t,{\bf Y}^t)
P(Xt,Yt)之间的距离,用
{
(
z
i
s
1
,
.
.
.
,
z
i
s
∣
L
∣
)
}
i
=
1
n
\{({\bf z}_i^{s1},...,{\bf z}_i^{s|\mathcal L|})\}_{i=1}^n
{(zis1,...,zis∣L∣)}i=1n与
{
(
z
i
t
1
,
.
.
.
,
z
i
t
∣
L
∣
)
}
j
=
1
m
\{({\bf z}_i^{t1},...,{\bf z}_i^{t|\mathcal L|})\}_{j=1}^m
{(zit1,...,zit∣L∣)}j=1m分别表示激活与适应层
L
\mathcal{L}
L,JMMD定义如下:
d
J
M
M
D
2
(
S
^
,
T
^
)
=
∥
E
i
∈
[
n
]
⊗
l
∈
L
ϕ
l
(
z
i
s
l
)
−
E
j
∈
[
m
]
⊗
l
∈
L
ϕ
l
(
z
j
t
l
)
∥
H
k
2
(27)
d_{\rm JMMD}^2(\mathcal{\hat S,\hat T})=\|\mathbb{E}_{i\in[n]}\otimes_{l\in\mathcal L}\phi^l({\bf z}_i^{sl})-\mathbb{E}_{j\in[m]}\otimes_{l\in\mathcal L}\phi^l({\bf z}_j^{tl})\|_{\mathcal H_k}^2\tag{27}
dJMMD2(S,T)=∥Ei∈[n]⊗l∈Lϕl(zisl)−Ej∈[m]⊗l∈Lϕl(zjtl)∥Hk2(27)
其中
ϕ
l
\phi^l
ϕl是关于核函数
k
l
k^l
kl和网络层
l
l
l的特征映射,
⊗
\otimes
⊗表示外积。
常用于MMD中的核函数是高斯核:
k
(
x
1
,
x
2
)
=
exp
(
−
∥
x
1
−
x
2
∥
2
2
σ
2
)
k({\bf x}_1,{\bf x}_2)=\exp\left(\frac{-\|{\bf x}_1-{\bf x}_2\|^2}{2\sigma^2}\right)
k(x1,x2)=exp(2σ2−∥x1−x2∥2)
通过泰勒展开可以将MMD表示为各阶统计动量(all orders of statistic moments)距离的加权和,基于这样的想法,参考文献
[
166
,
200
]
[166,200]
[166,200]对MMD做了一些近似的变体。
MMD的缺陷在它估计两个领域之间的距离时,无法将数据分布的几何信息考察进来,对该缺陷改进的研究包括参考文献
[
34
,
36
,
29
]
[34,36,29]
[34,36,29]
最后记录一些其他相关研究:
- 参考文献
[
102
]
[102]
[102]:直接通过对齐批标准化(BatchNorm)统计量来最小化领域距离,以缓解分布漂移问题。 - 参考文献
[
185
]
[185]
[185]:提出可迁移的标准化(transferable normalization,TransNorm),即通过具体领域分布的均值与标准差来捕获领域的充分统计量。 - 参考文献
[
84
]
[84]
[84]:提出对比适应网络(contrastive adaptation network,CAN),用的似乎是据类的方法,它是要缓解MMD和JMMD中不同类别样本不齐(misalign samples)的问题。
3.2.2 领域对立学习 Domain Adversarial Learning
-
领域对立神经网络(domain adversarial neural network,DANN,参考文献
[
45
,
46
]
[45,46]
[45,46]):DANN本身启发于对抗生成网络(generative adversarial net,GAN,参考文献
[
54
]
[54]
[54])对分布的建模思想。如Figure 20左图所示,DANN中包含两个模块,第一个模块领域辨识器(domain discriminator)
D
D
D训练用于区分源特征(source features)与目标特征(target features),第二个模块特征生成器(feature generator)
ψ
\psi
ψ训练用于生成特征以混淆
D
D
D。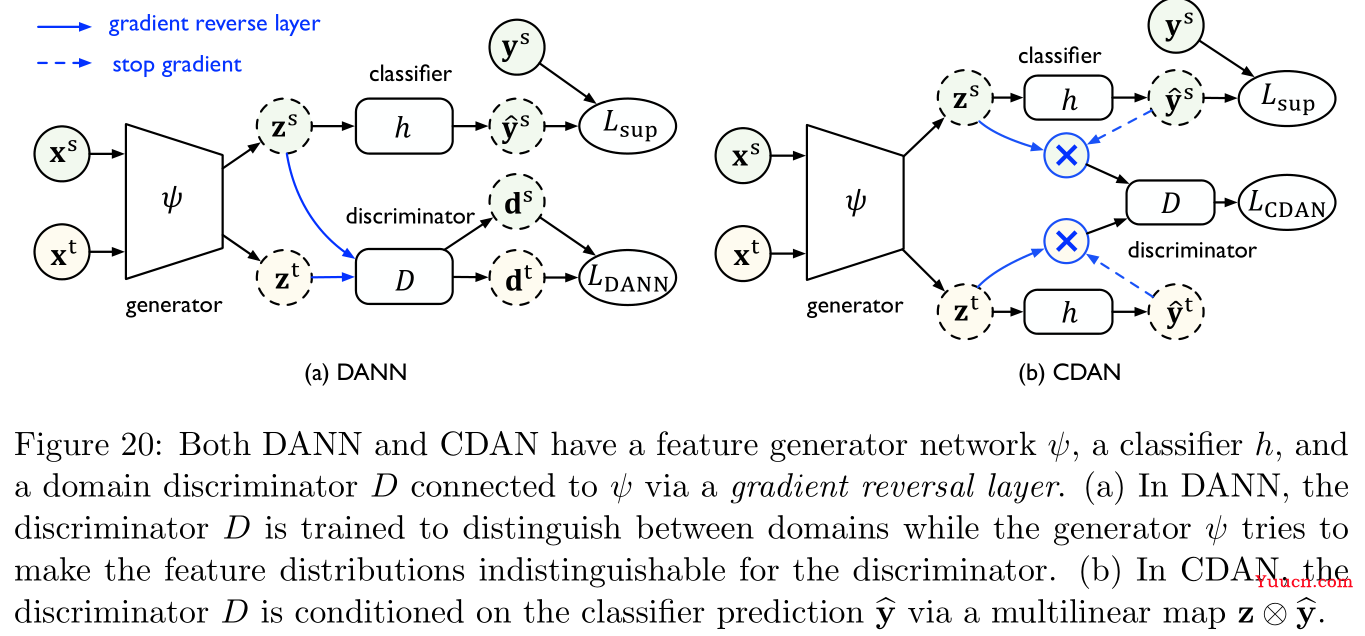
根据Section 3.2中关于
H
Δ
H
\mathcal{H\Delta H}
HΔH散度的结论,可以得出特征分布之间的
H
Δ
H
\mathcal{H\Delta H}
HΔH散度差距:
L
D
A
N
N
(
ψ
)
=
max
D
E
x
s
∼
S
^
log
[
D
(
z
s
)
]
+
E
x
t
∼
T
^
log
[
1
−
D
(
z
t
)
]
(28)
L_{\rm DANN}(\psi)=\max_D\mathbb{E}_{{\bf x}^s\sim\mathcal{\hat S}}\log[D({\bf z}^s)]+\mathbb{E}_{{\bf x}^t\sim\mathcal{\hat T}}\log[1-D({\bf z}^t)]\tag{28}
LDANN(ψ)=DmaxExs∼Slog[D(zs)]+Ext∼Tlog[1−D(zt)](28)
其中,
z
=
ψ
(
x
)
{\bf z}=\psi({\bf x})
z=ψ(x)是
x
{\bf x}
x的特征表示,特征生成器
ψ
\psi
ψ的目标函数是最小化源误差(source error)以及式
(
28
)
(28)
(28)中的
H
Δ
H
\mathcal{H\Delta H}
HΔH散度,如下所示:
min
ψ
,
h
E
(
x
s
,
y
s
)
∼
S
^
L
CE
(
h
(
z
s
)
,
y
s
)
+
λ
L
(
D
A
N
N
)
(
ψ
)
(29)
\min_{\psi,h}\mathbb{E}_{({\bf x}^s,{\bf y}^s)\sim\mathcal{\hat S}}L_{\text{CE}}(h({\bf z}^s),{\bf y}^s)+\lambda L(\rm DANN)(\psi)\tag{29}
ψ,hminE(xs,ys)∼SLCE(h(zs),ys)+λL(DANN)(ψ)(29)
其中
L
C
E
L_{\rm CE}
LCE是交叉熵损失,
λ
\lambda
λ是权衡两项的超参数。参考文献
[
115
]
[115]
[115]对式
(
28
)
(28)
(28)进行了改进,提出条件领域对立网络(conditional domain adversarial network,CDAN),即在分类器预测结果
y
^
=
h
(
z
)
{\bf \hat y}=h({\bf z})
y=h(z)的条件下考察
z
{\bf z}
z的概率分布,并引入多线性映射(multilinear map)
z
⊗
y
^
{\bf z}\otimes{\bf \hat y}
z⊗y来替代式
(
28
)
(28)
(28)中的
z
{\bf z}
z作为领域辨识器
D
D
D的输入:
L
C
D
A
N
(
ψ
)
=
max
D
E
x
s
∼
S
^
log
[
D
(
z
s
⊗
y
^
s
)
]
+
E
x
t
∼
T
^
log
[
1
−
D
(
z
t
⊗
y
^
t
)
]
(30)
L_{\rm CDAN}(\psi)=\max_D\mathbb{E}_{{\bf x}^s\sim\mathcal{\hat S}}\log[D({\bf z}^s\otimes{\bf \hat y}^s)]+\mathbb{E}_{{\bf x}^t\sim\mathcal{\hat T}}\log[1-D({\bf z}^t\otimes{\bf \hat y}^t)]\tag{30}
LCDAN(ψ)=DmaxExs∼Slog[D(zs⊗ys)]+Ext∼Tlog[1−D(zt⊗yt)](30)
式
(
30
)
(30)
(30)相较式
(
29
)
(29)
(29)的优势在于,CDAN可以完全捕获特征表示和分类器预测结果之间的交叉方差(cross-variance),因此可以得到更好的联合分布。 -
改进:参考文献
[
176
,
28
,
15
]
[176,28,15]
[176,28,15]-
参考文献
[
176
]
[176]
[176]:提出对立区分领域适应(adversarial discriminative domain adaptation,ADDA),解决的是DANN中可能出现的梯度消失问题,具体而言ADDA将特征生成器
ψ
\psi
ψ以及领域辨识器
D
D
D的优化过程划分为两个独立的部分,其中
D
D
D的部分与式
(
29
)
(29)
(29)相同,
ψ
\psi
ψ的部分转变为:
min
ψ
E
x
t
∼
T
^
−
log
[
D
(
z
t
)
]
(31)
\min_{\psi}\mathbb{E}_{{\bf x}^t\sim\mathcal{\hat T}}-\log[D({\bf z}^t)]\tag{31}
ψminExt∼T−log[D(zt)](31) -
参考文献
[
28
]
[28]
[28]:提出批量谱惩罚(batch spectral penalization,BSP),基于最大特征值对应的特征向量中包含了更多关于迁移的知识,因此设置关于最大奇异值的惩罚项用于增强特征分类效果,这个是关于图像处理的迁移模型。 -
参考文献
[
15
]
[15]
[15]:为每一个领域引入一个私有的子空间,用于保存具体领域的信息,这个也是关于图像处理的迁移研究。
-
-
领域对立学习在现实场景中的应用:
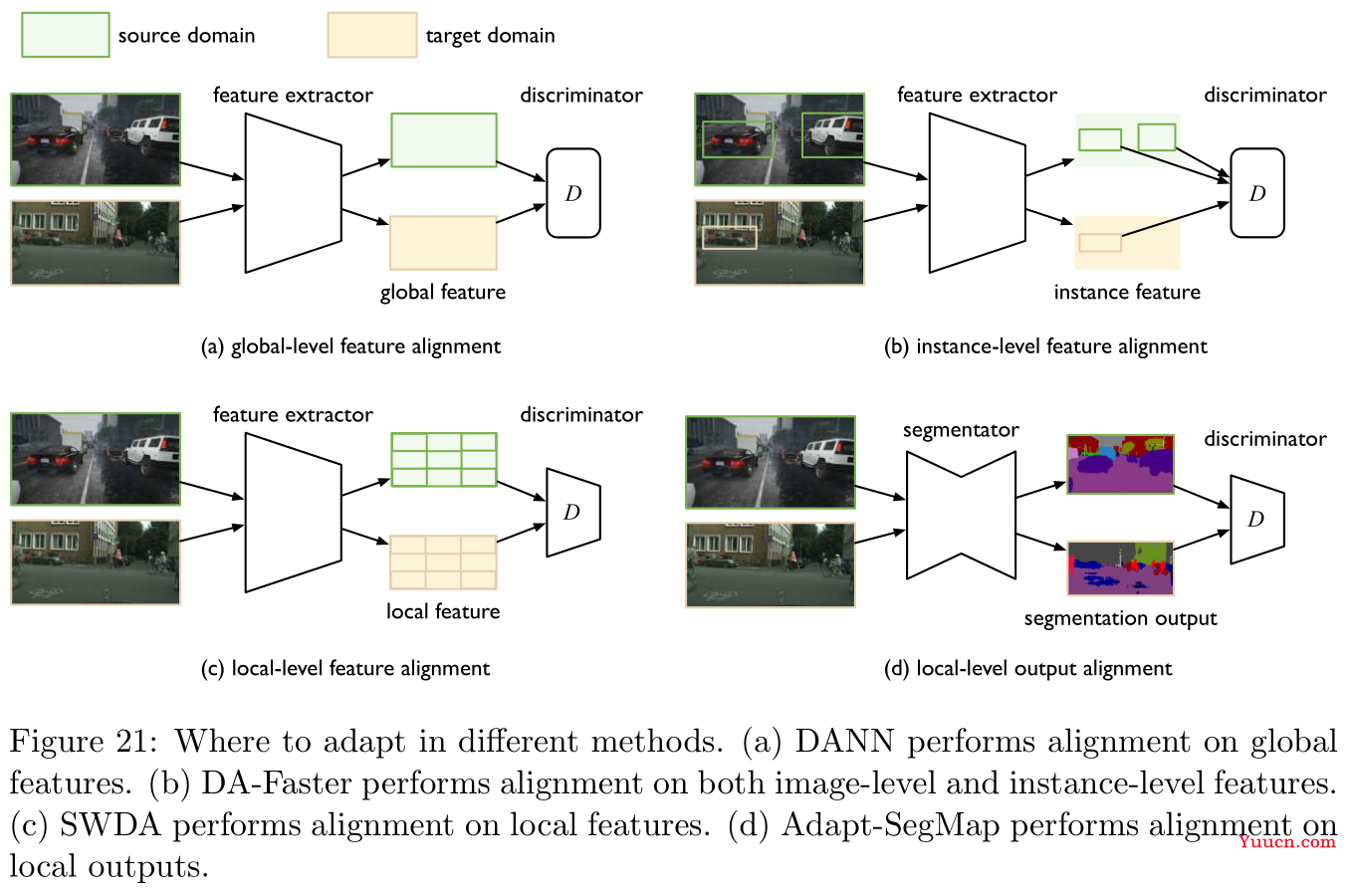
-
哪一部分应当进行适应是未知的(which part to adapt is unknown):
这里探讨的是图像处理领域。在图像识别中,我们只需要分类输入图像,然而在实体识别中,我们则需要先定位兴趣区域(region of interests,RoIs)然后再进行分类。由于不同领域存在分布漂移,因此目标领域中RoIs的位置是不可靠的,于是应当在对立训练中将的哪一部分进行适应是未知的。
参考文献
[
30
,
147
,
28
,
82
]
[30,147,28,82]
[30,147,28,82]基本都是围绕这一问题的解决展开的研究,其实有点类似上面正则化的操作,无非是针对特征进行对齐抑或是输出结果进行对齐,具体操作如Figure 21所示。 -
每个样本标签之间存在结构化依赖(there are structural dependencies between labels of each sample):
在语义划分(semantic segment,这是计算机视觉中的概念)以及分词分类(如命名实体识别,词性标注)等低级分类问题中,基于特征的适应往往并不是一个好选择(即直接将词嵌入作为适应),原因是每个像素或者每个分词的特征都是高维的,且一个样本中就会包含非常多的像素或者分词。然而,凡事都有两面性,在高级分类问题中,上述这些低级分类任务的输出空间通常包含了关于分布的丰富信息(如场景布局信息或者上下文信息),因此直接基于输出空间进行适应又是一个不错的选择。
相关研究包括参考文献
[
173
,
182
]
[173,182]
[173,182],Figure 21中的右下图对应参考文献
[
173
]
[173]
[173]
-
3.2.3 假设对立学习 Hypothesis Adversarial Learning
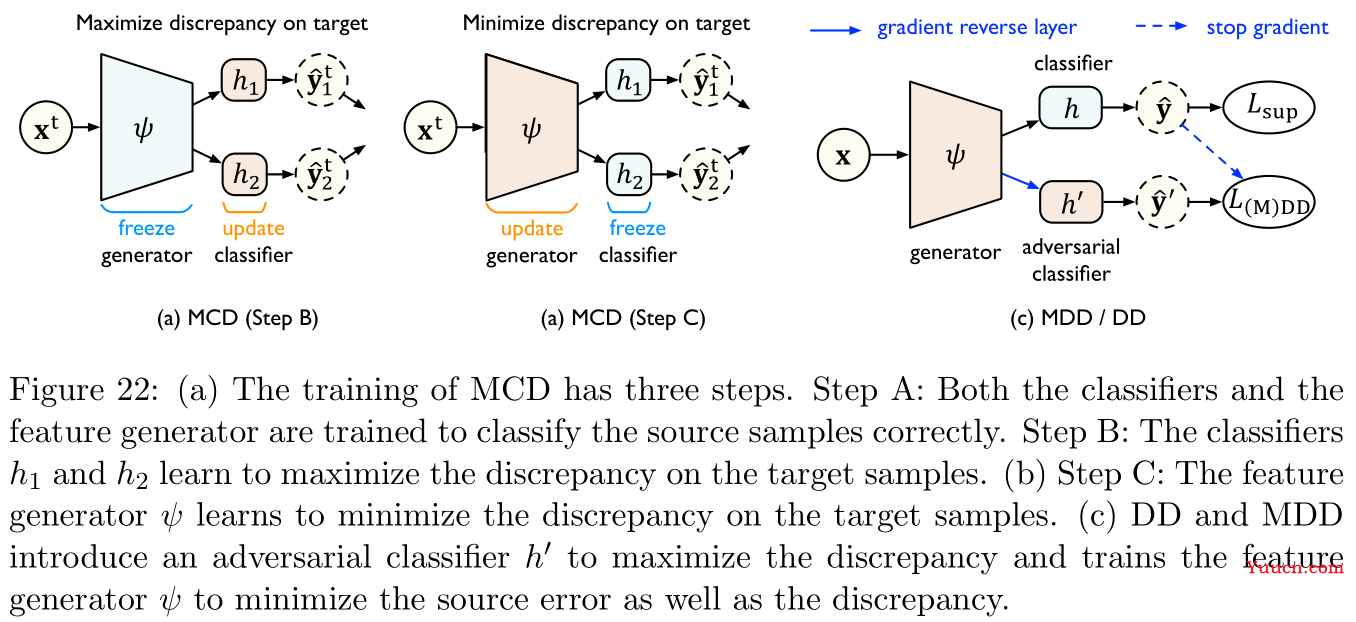
-
参考文献
[
146
]
[146]
[146]提出最大分类器差距(maximum classifier discrepancy,MCD)用于完全参数化的来估计与优化
H
Δ
H
\mathcal{H\Delta H}
HΔH散度,具体如Figure 22所示:- MCD最大化两个分类器输出之间的差距,并探测与源分布相差甚远的目标样本(即
H
Δ
H
\mathcal{H\Delta H}
HΔH散度)。 - 接下来一个特征生成器用于学习生成目标特征用于最小化领域差距。
- MCD使用的是
L
1
L_1
L1距离来衡量差距。 - 理论上MCD比
H
Δ
H
\mathcal{H\Delta H}
HΔH散度能得到更贴近的结果,然而实验表明其收敛速度缓慢且对超参数非常敏感。可能的原因是MCD中使用了两个任意分类器
h
h
h和
h
′
h'
h′来最大化差距,使得最小最大化(minimax)达到均衡相对困难。
- MCD最大化两个分类器输出之间的差距,并探测与源分布相差甚远的目标样本(即
-
参考文献
[
204
]
[204]
[204]提出的差距矛盾(disparity discrepancy,DD,上文中似乎已经提过)提供了一个更紧的上界,方法是通过在假设空间
H
\mathcal H
H上取上确界(而非
H
Δ
H
\mathcal H\Delta \mathcal H
HΔH),这显著使得最小最大化简单。如Figure 22所示,DD引入了一个对立分类器
h
′
h'
h′(与
h
h
h所属相同的假设空间),则
d
h
,
H
(
S
,
T
)
d_{h,\mathcal H}(\mathcal{S,T})
dh,H(S,T)的上确界近似为:
L
D
D
(
h
,
ψ
)
=
max
h
′
E
x
s
∼
S
^
L
s
[
h
′
(
ψ
(
x
s
)
)
,
h
(
ψ
(
x
s
)
)
]
−
E
x
t
∼
T
^
L
s
[
h
′
(
ψ
(
x
s
)
)
,
h
(
ψ
(
x
s
)
)
]
(32)
L_{\rm DD}(h,\psi)=\max_{h'}\mathbb{E}_{{\bf x}^s\sim\mathcal{\hat S}}L^s[h'(\psi({\bf x}^s)),h(\psi({\bf x}^s))]-\mathbb{E}_{{\bf x}^t\sim\mathcal{\hat T}}L^s[h'(\psi({\bf x}^s)),h(\psi({\bf x}^s))]\tag{32}
LDD(h,ψ)=h′maxExs∼SLs[h′(ψ(xs)),h(ψ(xs))]−Ext∼TLs[h′(ψ(xs)),h(ψ(xs))](32)
其中
L
s
L^s
Ls与
L
t
L^t
Lt是定义在源领域和目标领域上的损失函数。理论上对立分类器
h
′
h'
h′更贴近上确界,最小化下式可以降低目标误差
ϵ
T
\epsilon_{\mathcal T}
ϵT:
min
ψ
,
h
E
x
s
,
y
s
∼
S
^
L
C
E
(
h
(
ψ
(
x
s
)
)
,
y
s
)
+
λ
L
D
D
(
h
,
ψ
)
(33)
\min_{\psi,h}\mathbb{E}_{{\bf x}^s,{\bf y}^s\sim\mathcal{\hat S}}L_{\rm CE}(h(\psi({\bf x}^s)),{\bf y}^s)+\lambda L_{\rm DD}(h,\psi)\tag{33}
ψ,hminExs,ys∼SLCE(h(ψ(xs)),ys)+λLDD(h,ψ)(33)
其中
λ
\lambda
λ是权衡两项的系数。直觉上的解释是,DD在寻找一个对立分类器
h
′
h'
h′来正确预测源领域上的样本,并且能够在目标领域上得到与
h
h
h不同的预测,然后特征生成器
ψ
\psi
ψ被训练用于生成在这决策边界上的特征来避免发生这样的情况。 -
DD只能用于处理二分类问题,因此参考文献
[
204
]
[204]
[204]进一步推广到边际差距矛盾(margin disparity discrepancy,MDD)以处理多酚类的问题设定:
L
M
D
D
(
h
,
ψ
)
=
max
h
′
γ
E
x
s
∼
S
^
log
[
σ
h
(
ψ
(
x
s
)
)
(
h
′
(
ψ
(
x
s
)
)
)
]
+
E
x
t
∼
T
^
log
[
1
−
σ
h
(
ψ
(
x
t
)
)
(
h
′
(
ψ
(
x
t
)
)
)
]
(34)
L_{\rm MDD}(h,\psi)=\max_{h'}\gamma\mathbb{E}_{{\bf x}^s\sim\mathcal{\hat S}}\log[\sigma_{h(\psi({\bf x}^s))}(h'(\psi({\bf x}^s)))]+\mathbb{E}_{{\bf x}^t\sim\mathcal{\hat T}}\log[1-\sigma_{h(\psi({\bf x}^t))}(h'(\psi({\bf x}^t)))]\tag{34}
LMDD(h,ψ)=h′maxγExs∼Slog[σh(ψ(xs))(h′(ψ(xs)))]+Ext∼Tlog[1−σh(ψ(xt))(h′(ψ(xt)))](34)
其中
γ
=
exp
ρ
\gamma=\exp\rho
γ=expρ,
ρ
\rho
ρ为边际率,
σ
\sigma
σ是激活函数(如softmax),
γ
\gamma
γ的选取是非常关键的,能够有效避免对边界的高估。
3.2.4 领域翻译 Domain Translation
-
领域翻译(domain translation)指将原始数据(文本、图像、音频等)从源领域
S
\mathcal S
S映射到目标领域
T
\mathcal T
T中的一类任务。在领域适应性问题中,我们可以使用翻译模型(通常基于GAN)在目标领域中获得类似源领域样本的标签。 -
针对GAN,有很多不同变体的改进,如参考文献
[
106
]
[106]
[106]提出的成对对抗生成网络(coupled generative adversarial networks,CoGAN)学习多领域图片数据的联合分布,即多个不同的生成器需要生成成对的、不同领域的、标签共享的数据。CoGAN无需不同领域中对应的图像即可学习到联合分布,这些生成的共享标签的目标样本将被用于训练目标领域中的模型。 -
领域翻译的目标函数通常是学习一个映射
G
:
S
→
T
G:\mathcal{S}\rightarrow\mathcal{T}
G:S→T使得生成样本
G
(
x
)
G({\bf x})
G(x)与目标领域中的训练样本是不可区分的。如Figure 23所示,参考文献
[
16
]
[16]
[16]提出的的PixelDA引入一个对立辨识器
D
D
D来区分翻译得到的样本与目标样本:
L
G
A
N
(
G
)
=
max
D
E
x
∼
S
^
log
[
1
−
D
(
G
(
x
)
)
]
+
E
x
∼
T
^
log
[
D
(
x
)
]
(35)
L_{\rm GAN}(G)=\max_D\mathbb{E}_{{\bf x}\sim\mathcal{\hat S}}\log[1-D(G({\bf x}))]+\mathbb{E}_{{\bf x}\sim\mathcal{\hat T}}\log[D({\bf x})]\tag{35}
LGAN(G)=DmaxEx∼Slog[1−D(G(x))]+Ex∼Tlog[D(x)](35)
生成器
G
G
G试图希望使得
G
(
x
)
G({\bf x})
G(x)与目标领域中的样本尽可能的相似,因此接下来需要
min
G
L
G
A
N
(
G
)
\min_G L_{\rm GAN}(G)
minGLGAN(G)。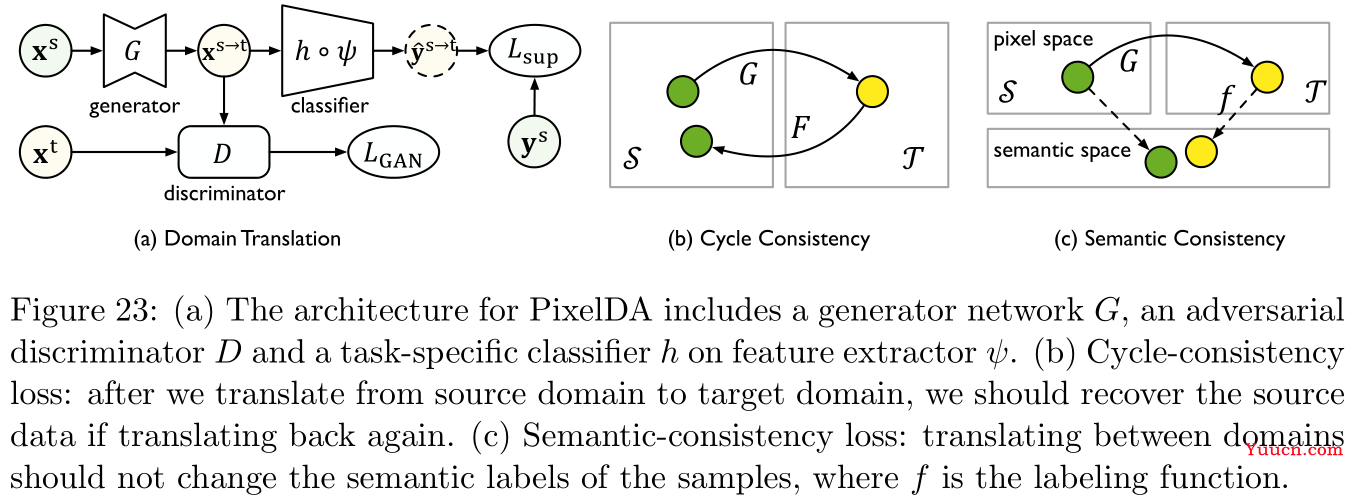
最终具体每个任务的分类器
f
f
f以及特征挖掘器
ψ
\psi
ψ通过有监督的训练(在生成数据上)通过:
min
ψ
,
h
E
(
x
,
y
)
∼
S
^
L
sup
(
h
∘
ψ
(
G
(
x
)
)
,
y
)
\min_{\psi,h}\mathbb{E}_{({\bf x},{\bf y})\sim\mathcal{\hat S}}L_{\sup}(h\circ\psi(G({\bf x})),{\bf y})
ψ,hminE(x,y)∼SLsup(h∘ψ(G(x)),y) -
周期一致性(cycle consistency):
GAN可以用于学习连个不同领域数据集之间的映射,这里有两个问题:
- 源领域的样本可能会映射成一个与目标领域无关的样本。
- 多个不同源领域的样本可能会映射成同一个目标领域样本,这回导致经典的模式坍塌(mode collapse,参考文献
[
54
]
[54]
[54])问题。
由此参考文献
[
209
]
[209]
[209]提出CycleGAN,引入了一个反向映射
F
:
T
→
S
F:\mathcal{T\rightarrow S}
F:T→S(从目标领域映射到源领域),再构建一个周期一致性的约束来缩小可能的映射函数空间(如Figure 23所示)。具体从数学表达上来看,周期一致性需要
F
F
F和
G
G
G两个映射是双射(bijections)且互为逆映射,即实际操作中
F
(
G
(
x
)
)
≈
x
,
G
(
F
(
x
)
)
≈
x
F(G({\bf x}))\approx{\bf x},G(F({\bf x}))\approx{\bf x}
F(G(x))≈x,G(F(x))≈x,这种思想已经被广泛应用于领域适应性问题中,如参考文献
[
72
,
189
,
17
,
85
,
92
,
33
]
[72,189,17,85,92,33]
[72,189,17,85,92,33],最后两篇是自然语言处理的,都是关于跨语言的机器翻译任务,前面四篇都是图像处理,包括图像分类、语义划分、身份识别、机器人抓取(robotic grasping),实体识别等。 -
语义一致性(semantic consistency):
从源领域映射标签到目标领域时容易发生标签翻转(label flipping)问题,由此引出的语义一致性指的是希望能够使得样本
x
\bf x
x于翻译得到的样本一致,即
f
(
x
)
=
f
(
G
(
x
)
)
f({\bf x})=f(G({\bf x}))
f(x)=f(G(x))。由于
f
f
f未知,因此参考文献
[
169
,
72
,
17
]
[169,72,17]
[169,72,17]提出了一系列代理函数(proxy function),即在给定代理函数
h
p
h_{\rm p}
hp与距离衡量方法
d
d
d的情况下,目标函数是为了减少语义的不一致性:
min
G
L
S
C
(
G
,
h
p
)
=
d
(
h
p
(
x
)
,
h
p
(
G
(
x
)
)
)
(36)
\min_GL_{\rm SC}(G,h_{\rm p})=d(h_{\rm p}({\bf x}),h_{\rm p}(G({\bf x})))\tag{36}
GminLSC(G,hp)=d(hp(x),hp(G(x)))(36) -
若领域的差异主要是低级的(如文本、描述、颜色等),翻译方法可以有效弥补领域差异,但是如果是高级的(如摄像机角度,camera angles),翻译方法通常不能起效。
3.2.5 半监督学习 Semi-Supervised Learning
-
无监督领域适应性(UDA)与半监督学习(SSL)密切相关,许多SSL方法都可以应用到UDA中。
-
半监督学习的三个假设:
-
平滑性假设(smoothness assumption):若两个样本
x
1
,
x
2
{\bf x}_1,{\bf x}_2
x1,x2在高密度区域中距离相近,则它们的输出
y
1
,
y
2
{\bf y}_1,{\bf y_2}
y1,y2同样应当相近。 - 簇假设(cluster assumption):若样本点处于同一个簇中,则它们大概率是同一类型。
- manifold假设( assumption):高维数据可以近似到一个低维manifold(这个单词似乎无法直译)中。
-
平滑性假设(smoothness assumption):若两个样本
-
可用于UDA的一些SSL方法:
-
一致性正则化(consistency regularization):指的是相似样本点应当得到一致的预测结果,相关研究包括参考文献
[
44
,
48
]
[44,48]
[44,48]。 -
熵最小化(entropy minimization):使模型对于未标注的数据做置信度最高的(即熵最低的)预测结果,常作为许多领域适应性方法的辅助方法,相关研究包括参考文献
[
82.104
]
[82.104]
[82.104]。 -
虚假标注(pseudo-labeling):为未标注的数据生成代理标签,并使用这些带噪声的标签与已标注的数据混合在一起进行训练。相关研究包括参考文献
[
212
,
201
,
205
]
[212,201,205]
[212,201,205],这里特别提到说交叉熵损失对噪声标签的敏感度很高,因此参考文献
[
143
,
105
]
[143,105]
[143,105]中提出推广的交叉熵损失(generalized cross-entropy,GCE)作为解决方案:
L
G
C
E
(
x
,
y
~
)
=
1
q
(
1
−
h
y
~
(
x
)
q
)
(37)
L_{\rm GCE}({\bf x},\tilde y)=\frac1q(1-h_{\tilde y}({\bf x})^q)\tag{37}
LGCE(x,y~)=q1(1−hy~(x)q)(37)
其中
q
∈
(
,
1
]
q\in(0,1]
q∈(0,1]是用于权衡交叉熵与平均绝对值误差两个损失函数的超参数。
-
3.2.6 注释 Remarks
总结一下本小节所有方法的性能:
| 方法 | 适应性能 | 数据功效 | 模态延展性 | 任务延展性 | 理论保证 |
|---|---|---|---|---|---|
| 统计匹配 | 差 | 优 | 优 | 中 | 优 |
| 领域对立学习 | 中 | 中 | 优 | 中 | 优 |
| 假设对立学习 | 优 | 中 | 优 | 中 | 优 |
| 领域翻译 | 中 | 差 | 差 | 优 | 差 |
| 半监督学习 | 中 | 中 | 中 | 差 | 差 |
字段说明:
- 适应性能(adaptation performance):下游任务中有大量标注数据时的模型性能。
- 数据功效(data efficiency):下游任务中只有少量数据时的模型性能。
- 模态延展性(modality scalability):能否用于多模态数据,如文本、图片、音像。
- 任务延展性(task scalability):能否轻松的将预训练模型迁移到不同下游任务中。
- 理论保证(theory guarantee):适应中目标领域的推广误差能否控制在一定界限内。
4 评估 Evaluation
4.1 数据集 Datasets
通用语言理解评估(general language understanding evaluation,GLUE,参考文献
[
183
]
[183]
[183])是目前自然语言处理领域中最又名的基准,下表例举了一系列GLUE的数据集,包括九个句子或句子对级别的语言理解任务:
| 语料集 | 训练数据量 | 测试数据量 | 评估指标 | 任务类型 | 领域 |
|---|---|---|---|---|---|
CoLA \text{CoLA} CoLA |
8.5 k 8.5\rm k 8.5k |
1 k 1\rm k 1k |
马修斯相关系数 | 可接受性 | 混合 |
SST-2 \text{SST-2} SST-2 |
67 k 67\rm k 67k |
1.8 k 1.8\rm k 1.8k |
精确度 | 情感分析 | 影评 |
MRPC \text{MRPC} MRPC |
3.7 k 3.7\rm k 3.7k |
1.7 k 1.7\rm k 1.7k |
精确度/ F1-score \text{F1-score} F1-score |
短语 | 新闻 |
STS-B \text{STS-B} STS-B |
7 k 7\rm k 7k |
1.4 k 1.4\rm k 1.4k |
皮尔逊相关系数 | 句子相似性 | 混合 |
QQP \text{QQP} QQP |
364 k 364\rm k 364k |
391 k 391\rm k 391k |
精确度/ F1-score \text{F1-score} F1-score |
短语 | 社交问答 |
MNLI \text{MNLI} MNLI |
393 k 393\rm k 393k |
20 k 20\rm k 20k |
(非)匹配精确度 | 自然语言推断 | 混合 |
QNLI \text{QNLI} QNLI |
105 k 105\rm k 105k |
5.4 k 5.4\rm k 5.4k |
精确度 | 问答/自然语言推断 | 维基百科 |
RTE \text{RTE} RTE |
2.5 k 2.5\rm k 2.5k |
3 k 3\rm k 3k |
精确度 | 自然语言推断 | 新闻与维基百科 |
WNLI \text{WNLI} WNLI |
634 634 634 |
146 146 146 |
精确度 | 共指/自然语言推断 | 科幻书 |
- 笔者注:最后一个数据集可能数据量少单位。
但是目前仍未形成类似GLUE用于计算机视觉的基准,这里只是例举一些图像处理领域的常用的数据集:
| 数据集 | 训练数据量 | 测试数据量 | 类别数 | 评估指标 | 领域 |
|---|---|---|---|---|---|
|
Food-101 \text{Food-101} Food-101(参考文献 [ 88 ] [88] [88]) |
75750 75750 75750 |
25250 25250 25250 |
101 101 101 |
top-1 \text{top-1} top-1 |
混合 |
|
CIFAR-10 \text{CIFAR-10} CIFAR-10(参考文献 [ 88 ] [88] [88]) |
50000 50000 50000 |
10000 10000 10000 |
10 10 10 |
top-1 \text{top-1} top-1 |
混合 |
|
cIFAR-100 \text{cIFAR-100} cIFAR-100(参考文献 [ 88 ] [88] [88]) |
50000 50000 50000 |
10000 10000 10000 |
100 100 100 |
top-1 \text{top-1} top-1 |
混合 |
|
SUN397 \text{SUN397} SUN397(参考文献 [ 88 ] [88] [88]) |
19850 19850 19850 |
19850 19850 19850 |
397 397 397 |
top-1 \text{top-1} top-1 |
混合 |
|
Stanford Cars \text{Stanford Cars} Stanford Cars(参考文献 [ 88 ] [88] [88]) |
8144 8144 8144 |
8041 8041 8041 |
196 196 196 |
top-1 \text{top-1} top-1 |
混合 |
|
FGVC Aircraft \text{FGVC Aircraft} FGVC Aircraft(参考文献 [ 88 ] [88] [88]) |
6667 6667 6667 |
3333 3333 3333 |
100 100 100 |
mean per-class \text{mean per-class} mean per-class |
混合 |
|
Describable Textures(DTD) \text{Describable Textures(DTD)} Describable Textures(DTD)(参考文献 [ 88 ] [88] [88]) |
3760 3760 3760 |
1880 1880 1880 |
47 47 47 |
top-1 \text{top-1} top-1 |
混合 |
|
Oxford-III Pets \text{Oxford-III Pets} Oxford-III Pets(参考文献 [ 88 ] [88] [88]) |
3680 3680 3680 |
3369 3369 3369 |
37 37 37 |
mean per-class \text{mean per-class} mean per-class |
混合 |
|
Caltech-101 \text{Caltech-101} Caltech-101(参考文献 [ 88 ] [88] [88]) |
3060 3060 3060 |
6084 6084 6084 |
102 102 102 |
mean per-class \text{mean per-class} mean per-class |
混合 |
Oxford 102 flowers \text{Oxford 102 flowers} Oxford 102 flowers |
2040 2040 2040 |
6149 6149 6149 |
102 102 102 |
top-1 \text{top-1} top-1 |
混合 |
|
ImageNet-R \text{ImageNet-R} ImageNet-R(参考文献 [ 69 ] [69] [69]) |
− - − |
30 k 30\rm k 30k |
200 200 200 |
top-1 \text{top-1} top-1 |
混合 |
|
ImageNet-Sketch \text{ImageNet-Sketch} ImageNet-Sketch(参考文献 [ 84 ] [84] [84]) |
− - − |
50 k 50\rm k 50k |
1000 1000 1000 |
top-1 \text{top-1} top-1 |
草稿 |
|
DomainNet-c \text{DomainNet-c} DomainNet-c(参考文献 [ 128 ] [128] [128]) |
33525 33525 33525 |
14604 14604 14604 |
365 365 365 |
top-1 \text{top-1} top-1 |
剪贴画 |
|
DomainNet-p \text{DomainNet-p} DomainNet-p(参考文献 [ 128 ] [128] [128]) |
50416 50416 50416 |
21850 21850 21850 |
365 365 365 |
top-1 \text{top-1} top-1 |
油画 |
|
DomainNet-r \text{DomainNet-r} DomainNet-r(参考文献 [ 128 ] [128] [128]) |
120906 120906 120906 |
52041 52041 52041 |
365 365 365 |
top-1 \text{top-1} top-1 |
混合 |
|
DomainNet-s \text{DomainNet-s} DomainNet-s(参考文献 [ 128 ] [128] [128]) |
48212 48212 48212 |
20916 20916 20916 |
365 365 365 |
top-1 \text{top-1} top-1 |
草稿 |
4.2 开源包 Library
-
项目地址:GitHub@TLlib(进行中)
-
使用方法:官方文档@TLlib
下面是一个简单的DANN应用的代码示例:
# define the domain discriminator from dalib.modules.domain_discriminator import DomainDiscriminator discriminator = DomainDiscriminator(in_feature=1024, hidden_size=1024) # define the domain adversarial loss module from dalib.adptation.dann import DomainAdversarialLoss dann = DomainAdversarialLoss(discriminator, reduction='mean') # features from the source and target domain f_s, f_t = torch.randn(20, 1024), torch.randn(20, 1024) # calculate the final loss loss = dann(f_s, f_t) -
目前TLlib主要是以PyTorch作为后端进行的实现,具有较好的可延展性。
4.3 基准 Benchmark
本节主要是对Section 4.1中提到的若干大规模数据集上的预训练和适应的典型方法的基准进行的展示,部分基准结果是通过TLlib实现得到的。
4.3.1 预训练 Pre-Training
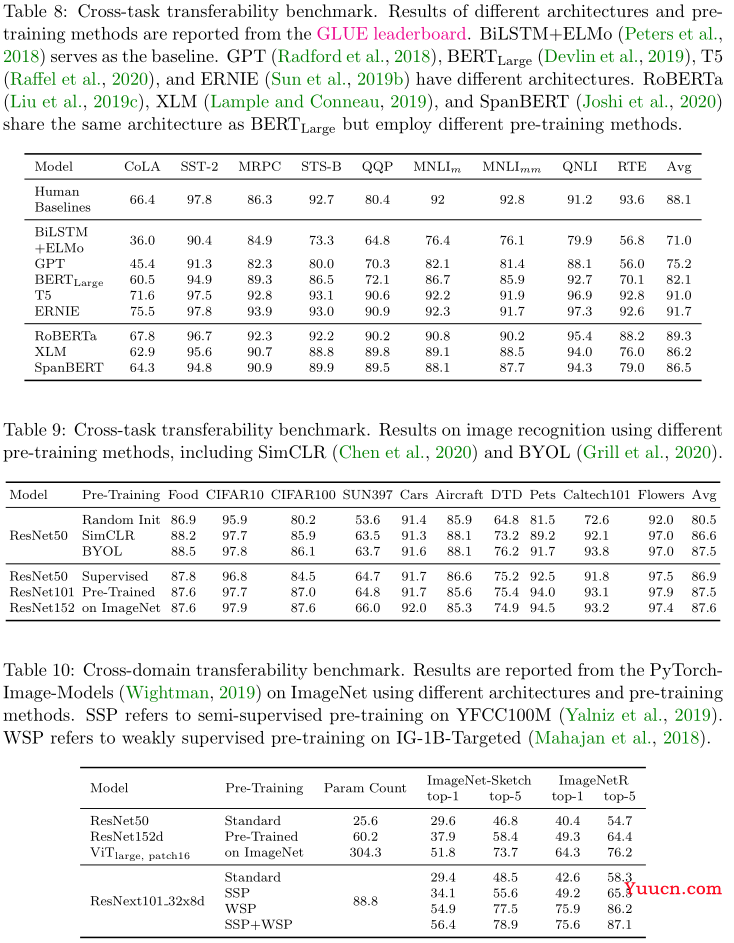
4.3.2 任务适应性 Task Adaptation
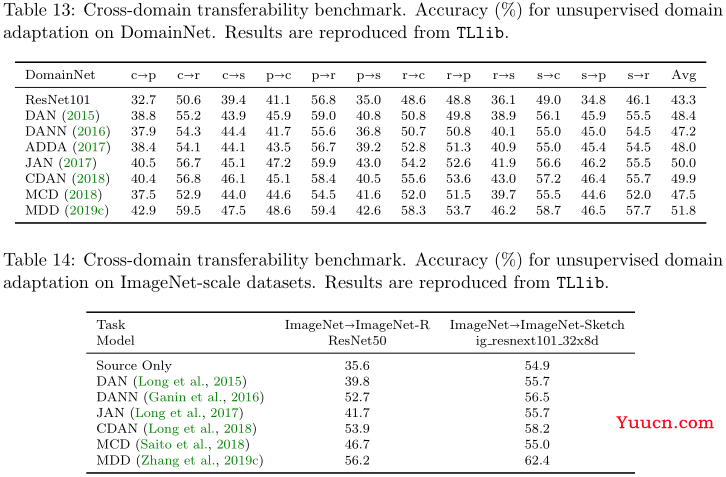
4.3.3 领域适应性 Domain Adaptation
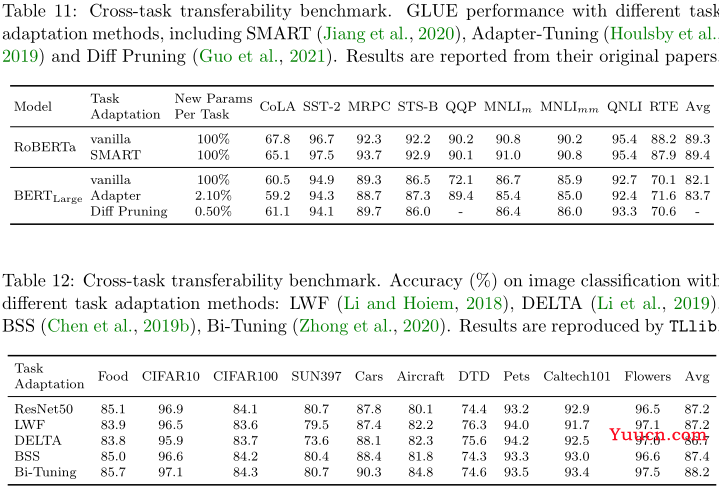
5 结论 Conclusion
In this paper, we investigate how to acquire and apply transferability in the whole lifecycle of deep learning. In the pre-training section, we focus on how to improve the transferability of the pre-trained models by designing architecture, pre-training task, and training strategy. In the task adaptation section, we discuss how to better preserve and utilize the transferable knowledge to improve the performance of target tasks. In the domain adaptation section, we illustrate how to bridge the domain gap to increase the transferability for real applications. This survey connects many isolated areas with their relation to transferability and provides a unified perspective to explore transferability in deep learning. We expect this study will attract the community’s attention to the fundamental role of transferability in deep learning.
参考文献
[001] Samira Abnar, Mostafa Dehghani, Behnam Neyshabur, and Hanie Sedghi. Exploring the limits of large scale pre-training. In ICLR, 2022.
[002] Armen Aghajanyan, Luke Zettlemoyer, and Sonal Gupta. Intrinsic dimensionality explains the effectiveness of language model fine-tuning. In ACL, 2021.
[003] Dario Amodei, Sundaram Ananthanarayanan, Rishita Anubhai, Jingliang Bai, Eric Battenberg, Carl Case, Jared Casper, Bryan Catanzaro, Qiang Cheng, Guoliang Chen, et al. Deep speech 2: End-to-end speech recognition in english and mandarin. In ICML, 2016.
[004] Martin Arjovsky, L´eon Bottou, Ishaan Gulrajani, and David Lopez-Paz. Invariant risk minimization. arXiv preprint arXiv:1907.02893, 2019.
[005] Sanjeev Arora, Rong Ge, Yingyu Liang, Tengyu Ma, and Yi Zhang. Generalization and equilibrium in generative adversarial nets (GANs). In ICML, 2017.
[006] Peter L. Bartlett and Shahar Mendelson. Rademacher and gaussian complexities: Risk bounds and structural results. In JMLR, 2002.
[007] Iz Beltagy, Kyle Lo, and Arman Cohan. Scibert: Pretrained language model for scientific text. In EMNLP, 2019.
[008] S. Ben-David, J. Blitzer, K. Crammer, A. Kulesza, F. Pereira, and J. W. Vaughan. A theory of learning from different domains. Machine Learning, 79, page 151–175, 2010a.
[009] Shai Ben-David, John Blitzer, Koby Crammer, and Fernando Pereira. Analysis of representations for domain adaptation. In NeurIPS, 2006.
[010] Shai Ben-David, Tyler Lu, Teresa Luu, and David Pal. Impossibility theorems for domain adaptation. In AISTATS, pages 129–136, 2010b.
[011] Yoshua Bengio. Deep learning of representations for unsupervised and transfer learning. In ICML workshop, 2012.
[012] Yoshua Bengio, Pascal Lamblin, Dan Popovici, and Hugo Larochelle. Greedy layer-wise training of deep networks. In NeurIPS, 2007.
[013] Yoshua Bengio, Aaron Courville, and Pascal Vincent. Representation learning: A review and new perspectives. TPAMI, 35(8):1798–1828, 2013.
[014] Yoshua Bengio, Yann Lecun, and Geoffrey Hinton. Deep learning for ai. Communications of the ACM, 64(7):58–65, 2021.
[015] Konstantinos Bousmalis, George Trigeorgis, Nathan Silberman, Dilip Krishnan, and Dumitru Erhan. Domain separation networks. In NeurIPS, 2016.
[016] Konstantinos Bousmalis, Nathan Silberman, David Dohan, Dumitru Erhan, and Dilip Krishnan. Unsupervised pixel-level domain adaptation with generative adversarial networks. In CVPR, 2017.
[017] Konstantinos Bousmalis, Alex Irpan, Paul Wohlhart, Yunfei Bai, Matthew Kelcey, Mrinal Kalakrishnan, Laura Downs, Julian Ibarz, Peter Pastor, Kurt Konolige, Sergey Levine, and Vincent Vanhoucke. Using simulation and domain adaptation to improve efficiency of deep robotic grasping. In ICRA, 2018.
[018] Tom B Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, et al. Language models are few-shot learners. In NeurIPS, 2020.
[019] Pau Panareda Busto and Juergen Gall. Open set domain adaptation. In ICCV, 2017.
[020] Rich Caruana. Multitask learning. Technical report, 1997.
[021] Olivier Chapelle, Bernhard Sch¨olkopf, and Alexander Zien. Semi-Supervised Learning (Adaptive Computation and Machine Learning). The MIT Press, 2006. ISBN 0262033585.
[022] Minmin Chen, Zhixiang Xu, Kilian Q. Weinberger, and Fei Sha. Marginalized denoising autoencoders for domain adaptation. In ICML, 2012.
[023] Ting Chen, Simon Kornblith, Mohammad Norouzi, and Geoffrey Hinton. A simple framework for contrastive learning of visual representations. In ICML, 2020.
[024] Wei-Yu Chen, Yen-Cheng Liu, Zsolt Kira, Yu-Chiang Frank Wang, and Jia-Bin Huang. A closer look at few-shot classification. In ICLR, 2019a.
[025] Xinlei Chen and Kaiming He. Exploring simple siamese representation learning. In CVPR, 2021.
[026] Xinlei Chen, Saining Xie, and Kaiming He. An empirical study of training self-supervised vision transformers. arXiv preprint arXiv:2104.02057, 2021a.
[027] Xinyang Chen, Sinan Wang, Bo Fu, Mingsheng Long, and Jianmin Wang. Catastrophic forgetting meets negative transfer: Batch spectral shrinkage for safe transfer learning. In NeurIPS, 2019b.
[028] Xinyang Chen, Sinan Wang, Mingsheng Long, and Jianmin Wang. Transferability vs. discriminability: Batch spectral penalization for adversarial domain adaptation. In ICML, 2019c.
[029] Xinyang Chen, Sinan Wang, Jianmin Wang, and Mingsheng Long. Representation subspace distance for domain adaptation regression. In ICML, 2021b.
[030] Yuhua Chen, Wen Li, Christos Sakaridis, Dengxin Dai, and Luc Van Gool. Domain adaptive faster R-CNN for object detection in the wild. In CVPR, 2018.
[031] Kyunghyun Cho, Bart van Merri¨enboer, Caglar Gulcehre, Dzmitry Bahdanau, Fethi Bougares, Holger Schwenk, and Yoshua Bengio. Learning phrase representations using RNN encoder–decoder for statistical machine translation. In EMNLP, 2014.
[032] Alexandra Chronopoulou, Christos Baziotis, and Alexandros Potamianos. An embarrassingly simple approach for transfer learning from pretrained language models. In NAACL, 2019.
[033] Alexis Conneau, Guillaume Lample, Ruty Rinott, Adina Williams, Samuel R. Bowman, Holger Schwenk, and Veselin Stoyanov. XNLI: evaluating cross-lingual sentence representations. In EMNLP, 2018.
[034] Nicolas Courty, R´emi Flamary, Amaury Habrard, and Alain Rakotomamonjy. Joint distribution optimal transportation for domain adaptation. In NeurIPS, 2017.
[035] Yin Cui, Yang Song, Chen Sun, Andrew Howard, and Serge Belongie. Large scale finegrained categorization and domain-specific transfer learning. In CVPR, pages 4109–4118, 2018.
[036] Bharath Bhushan Damodaran, Benjamin Kellenberger, R´emi Flamary, Devis Tuia, and Nicolas Courty. Deepjdot: Deep joint distribution optimal transport for unsupervised domain adaptation. In ECCV, 2018.
[037] Matthias Delange, Rahaf Aljundi, Marc Masana, Sarah Parisot, Xu Jia, Ales Leonardis, Greg Slabaugh, and Tinne Tuytelaars. A continual learning survey: Defying forgetting in classification tasks. TPAMI, page 1–20, 2021.
[038] Jia Deng, Wei Dong, Richard Socher, Li-Jia Li, Kai Li, and Li Fei-Fei. Imagenet: A largescale hierarchical image database. In CVPR, 2009.
[039] Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. Bert: Pre-training of deep bidirectional transformers for language understanding. In NAACL, 2019.
[040] Carl Doersch, Abhinav Gupta, and Alexei A. Efros. Unsupervised visual representation learning by context prediction. In ICCV, 2015.
[041] Jeff Donahue, Yangqing Jia, Oriol Vinyals, Judy Hoffman, Ning Zhang, Eric Tzeng, and Trevor Darrell. Decaf: A deep convolutional activation feature for generic visual recognition. In ICML, 2014.
[042] Alexey Dosovitskiy, Lucas Beyer, Alexander Kolesnikov, Dirk Weissenborn, Xiaohua Zhai, Thomas Unterthiner, Mostafa Dehghani, Matthias Minderer, Georg Heigold, Sylvain Gelly, Jakob Uszkoreit, and Neil Houlsby. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. In ICLR, 2021.
[043] Chelsea Finn, Pieter Abbeel, and Sergey Levine. Model-agnostic meta-learning for fast adaptation of deep networks. In ICML, 2017.
[044] Geoffrey French, Michal Mackiewicz, and Mark H. Fisher. Self-ensembling for domain adaptation. In ICLR, 2018.
[045] Yaroslav Ganin and Victor Lempitsky. Unsupervised domain adaptation by backpropagation. In ICML, 2015.
[046] Yaroslav Ganin, Evgeniya Ustinova, Hana Ajakan, Pascal Germain, Hugo Larochelle, Fran¸cois Laviolette, Mario March, and Victor Lempitsky. Domain-adversarial training of neural networks. JMLR, 17(59):1–35, 2016.
[047] Victor Garcia and Joan Bruna. Few-shot learning with graph neural networks. In ICLR, 2018.
[048] Yixiao Ge, Dapeng Chen, and Hongsheng Li. Mutual mean-teaching: Pseudo label refinery for unsupervised domain adaptation on person re-identification. In ICLR, 2020.
[049] Robert Geirhos, Patricia Rubisch, Claudio Michaelis, Matthias Bethge, Felix A Wichmann, and Wieland Brendel. Imagenet-trained cnns are biased towards texture; increasing shape bias improves accuracy and robustness. In ICLR, 2019.
[050] Ross Girshick, Jeff Donahue, Trevor Darrell, and Jitendra Malik. Rich feature hierarchies for accurate object detection and semantic segmentation. In CVPR, 2014.
[051] Xavier Glorot, Antoine Bordes, and Yoshua Bengio. Domain adaptation for large-scale sentiment classification: A deep learning approach. In ICML, 2011.
[052] Boqing Gong, Yuan Shi, Fei Sha, and Kristen Grauman. Geodesic flow kernel for unsupervised domain adaptation. In CVPR, 2012.
[053] Boqing Gong, Kristen Grauman, and Fei Sha. Connecting the dots with landmarks: Discriminatively learning domain-invariant features for unsupervised domain adaptation. In ICML, 2013.
[054] Ian J Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. Generative adversarial networks. In NeurIPS, 2014.
[055] Ian J Goodfellow, Jonathon Shlens, and Christian Szegedy. Explaining and harnessing adversarial examples. 2015.
[056] Anirudh Goyal, Alex Lamb, Jordan Hoffmann, Shagun Sodhani, Sergey Levine, Yoshua Bengio, and Bernhard Sch¨olkopf. Recurrent independent mechanisms. In ICLR, 2021.
[057] Arthur Gretton, Karsten M. Borgwardt, Malte J. Rasch, Bernhard Sch¨olkopf, and Alexander Smola. A kernel two-sample test. JMLR, 13(25):723–773, 2012a.
[058] Arthur Gretton, Dino Sejdinovic, Heiko Strathmann, Sivaraman Balakrishnan, Massimiliano Pontil, Kenji Fukumizu, and Bharath K Sriperumbudur. Optimal kernel choice for large-scale two-sample tests. In NeurIPS, 2012b.
[059] Jean-Bastien Grill, Florian Strub, Florent Altch´e, Corentin Tallec, Pierre Richemond, Elena Buchatskaya, Carl Doersch, Bernardo Avila Pires, Zhaohan Guo, Mohammad Gheshlaghi Azar, Bilal Piot, koray kavukcuoglu, Remi Munos, and Michal Valko. Bootstrap your own latent - a new approach to self-supervised learning. In NeurIPS, 2020.
[060] Ishaan Gulrajani and David Lopez-Paz. In search of lost domain generalization. In ICLR, 2021.
[061] Demi Guo, Alexander Rush, and Yoon Kim. Parameter-efficient transfer learning with diff pruning. In ACL, 2021.
[062] Yunhui Guo, Honghui Shi, Abhishek Kumar, Kristen Grauman, Tajana Rosing, and Rogerio Feris. Spottune: transfer learning through adaptive fine-tuning. In CVPR, 2019.
[063] Suchin Gururangan, Ana Marasovi´c, Swabha Swayamdipta, Kyle Lo, Iz Beltagy, Doug Downey, and Noah A. Smith. Don’t stop pretraining: Adapt language models to domains and tasks. In ACL, 2020.
[064] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In CVPR, 2016.
[065] Kaiming He, Georgia Gkioxari, Piotr Doll´ar, and Ross Girshick. Mask r-cnn. In ICCV, 2017.
[066] Kaiming He, Ross Girshick, and Piotr Doll´ar. Rethinking imagenet pre-training. In ICCV, 2019.
[067] Kaiming He, Haoqi Fan, Yuxin Wu, Saining Xie, and Ross Girshick. Momentum contrast for unsupervised visual representation learning. In CVPR, 2020.
[068] Kaiming He, Xinlei Chen, Saining Xie, Yanghao Li, Piotr Doll´ar, and Ross Girshick. Masked autoencoders are scalable vision learners. arXiv preprint arXiv:2111.06377, 2021.
[069] Dan Hendrycks, Steven Basart, Norman Mu, Saurav Kadavath, Frank Wang, Evan Dorundo, Rahul Desai, Tyler Zhu, Samyak Parajuli, Mike Guo, Dawn Song, Jacob Steinhardt, and Justin Gilmer. The many faces of robustness: A critical analysis of out-ofdistribution generalization. ICCV, 2021.
[070] R Devon Hjelm, Alex Fedorov, Samuel Lavoie-Marchildon, Karan Grewal, Phil Bachman, Adam Trischler, and Yoshua Bengio. Learning deep representations by mutual information estimation and maximization. In ICLR, 2019.
[071] Judy Hoffman, Dequan Wang, Fisher Yu, and Trevor Darrell. Fcns in the wild: Pixel-level adversarial and constraint-based adaptation. 2016.
[072] Judy Hoffman, Eric Tzeng, Taesung Park, Jun-Yan Zhu, Phillip Isola, Kate Saenko, Alexei Efros, and Trevor Darrell. Cycada: Cycle-consistent adversarial domain adaptation. In ICML, 2018.
[073] Neil Houlsby, Andrei Giurgiu, Stanislaw Jastrzebski, Bruna Morrone, Quentin De Laroussilhe, Andrea Gesmundo, Mona Attariyan, and Sylvain Gelly. Parameter-efficient transfer learning for NLP. In ICML, 2019.
[074] Jeremy Howard and Sebastian Ruder. Universal language model fine-tuning for text classification. In ACL, 2018.
[075] Weihua Hu, Bowen Liu, Joseph Gomes, Marinka Zitnik, Percy Liang, Vijay S. Pande, and Jure Leskovec. Pre-training graph neural networks. In ICLR, 2020.
[076] Jiayuan Huang, Arthur Gretton, Karsten Borgwardt, Bernhard Sch¨olkopf, and Alex Smola. Correcting sample selection bias by unlabeled data. In NeurIPS, 2007.
[077] Sergey Ioffe and Christian Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In ICML, 2015.
[078] Yunhun Jang, Hankook Lee, Sung Ju Hwang, and Jinwoo Shin. Learning what and where to transfer. In ICML, 2019.
[079] Haoming Jiang, Pengcheng He, Weizhu Chen, Xiaodong Liu, Jianfeng Gao, and Tuo Zhao. SMART: robust and efficient fine-tuning for pre-trained natural language models through principled regularized optimization. In ACL, 2020.
[080] Junguang Jiang, Yifei Ji, Ximei Wang, Yufeng Liu, Jianmin Wang, and Mingsheng Long. Regressive domain adaptation for unsupervised keypoint detection. In CVPR, 2021.
[081] Junguang Jiang, Baixu Chen, Jianmin Wang, and Mingsheng Long. Decoupled adaptation for cross-domain object detection. In ICLR, 2022.
[082] Ying Jin, Ximei Wang, Mingsheng Long, and Jianmin Wang. Minimum class confusion for versatile domain adaptation. In ECCV, 2020.
[083] Mandar Joshi, Danqi Chen, Yinhan Liu, Daniel S. Weld, Luke Zettlemoyer, and Omer Levy. SpanBERT: Improving pre-training by representing and predicting spans. In TACL, 2020.
[084] Guoliang Kang, Lu Jiang, Yi Yang, and Alexander G Hauptmann. Contrastive adaptation network for unsupervised domain adaptation. In CVPR, 2019.
[085] Taekyung Kim, Minki Jeong, Seunghyeon Kim, Seokeon Choi, and Changick Kim. Diversify and match: A domain adaptive representation learning paradigm for object detection. In CVPR, 2019.
[086] James Kirkpatrick, Razvan Pascanu, Neil Rabinowitz, Joel Veness, Guillaume Desjardins, Andrei A Rusu, Kieran Milan, John Quan, Tiago Ramalho, Agnieszka GrabskaBarwinska, et al. Overcoming catastrophic forgetting in neural networks. PNAS, 114 (13):3521–3526, 2017.
[087] Alexander Kolesnikov, Lucas Beyer, Xiaohua Zhai, Joan Puigcerver, Jessica Yung, Sylvain Gelly, and Neil Houlsby. Big transfer (bit): General visual representation learning. In ECCV, 2020.
[088] Simon Kornblith, Jonathon Shlens, and Quoc V Le. Do better imagenet models transfer better? In CVPR, 2019.
[089] Zhi Kou, Kaichao You, Mingsheng Long, and Jianmin Wang. Stochastic normalization. In NeurIPS, 2020.
[090] Alex Krizhevsky, Ilya Sutskever, and Geoffrey E. Hinton. Imagenet classification with deep convolutional neural networks. In NeurIPS, 2012.
[091] Guillaume Lample and Alexis Conneau. Cross-lingual language model pretraining. In NeurIPS, 2019.
[092] Guillaume Lample, Ludovic Denoyer, and Marc’Aurelio Ranzato. Unsupervised machine translation using monolingual corpora only. In ICLR, 2017.
[093] Zhenzhong Lan, Mingda Chen, Sebastian Goodman, Kevin Gimpel, Piyush Sharma, and Radu Soricut. Albert: A lite bert for self-supervised learning of language representations. In ICLR, 2020.
[094] Yann LeCun, Yoshua Bengio, and Geoffrey Hinton. Deep learning. Nature, 521(7553): 436–444, 2015.
[095] Chen-Yu Lee, Tanmay Batra, Mohammad Haris Baig, and Daniel Ulbricht. Sliced wasserstein discrepancy for unsupervised domain adaptation. In CVPR, 2019.
[096] Cheolhyoung Lee, Kyunghyun Cho, and Wanmo Kang. Mixout: Effective regularization to finetune large-scale pretrained language models. In ICLR, 2020a.
[097] Jinhyuk Lee, Wonjin Yoon, Sungdong Kim, Donghyeon Kim, Sunkyu Kim, Chan Ho So, and Jaewoo Kang. Biobert: a pre-trained biomedical language representation model for biomedical text mining. Bioinformatics, 36(4):1234–1240, 2020b.
[098] Mike Lewis, Yinhan Liu, Naman Goyal, Marjan Ghazvininejad, Abdelrahman Mohamed, Omer Levy, Veselin Stoyanov, and Luke Zettlemoyer. BART: Denoising Sequence-toSequence Pre-training for Natural Language Generation, Translation, and Comprehension. In ACL, 2020.
[099] Chunyuan Li, Heerad Farkhoor, Rosanne Liu, and Jason Yosinski. Measuring the intrinsic dimension of objective landscapes. In ICLR, 2018.
[100] Xiang Lisa Li and Percy Liang. Prefix-tuning: Optimizing continuous prompts for generation. In ACL, 2021.
[101] Xingjian Li, Haoyi Xiong, Hanchao Wang, Yuxuan Rao, Liping Liu, Zeyu Chen, and Jun Huan. Delta: Deep learning transfer using feature map with attention for convolutional networks. In ICLR, 2019.
[102] Yanghao Li, Naiyan Wang, Jianping Shi, Jiaying Liu, and Xiaodi Hou. Revisiting batch normalization for practical domain adaptation. In ICLR Workshop, 2017.
[103] Zhizhong Li and Derek Hoiem. Learning without forgetting. TPAMI, 40(12):2935–2947, 2018.
[104] Jian Liang, Dapeng Hu, and Jiashi Feng. Do we really need to access the source data? source hypothesis transfer for unsupervised domain adaptation. In ICML, 2020.
[105] Hong Liu, Jianmin Wang, and Mingsheng Long. Cycle self-training for domain adaptation. In NeurIPS, 2021a.
[106] Ming-Yu Liu and Oncel Tuzel. Coupled generative adversarial networks. In NeurIPS, 2016.
[107] Pengfei Liu, Weizhe Yuan, Jinlan Fu, Zhengbao Jiang, Hiroaki Hayashi, and Graham Neubig. Pre-train, prompt, and predict: A systematic survey of prompting methods in natural language processing, 2021b.
[108] Xiaodong Liu, Pengcheng He, Weizhu Chen, and Jianfeng Gao. Multi-task deep neural networks for natural language understanding. In ACL, 2019a.
[109] Yinhan Liu, Myle Ott, Naman Goyal, Jingfei Du, Mandar Joshi, Danqi Chen, Omer Levy, Mike Lewis, Luke Zettlemoyer, and Veselin Stoyanov. Roberta: A robustly optimized bert pretraining approach. arXiv preprint arXiv:1907.11692, 2019b.
[110] Yinhan Liu, Myle Ott, Naman Goyal, Jingfei Du, Mandar Joshi, Danqi Chen, Omer Levy, Mike Lewis, Luke Zettlemoyer, and Veselin Stoyanov. Roberta: A robustly optimized BERT pretraining approach. 2019c.
[111] Mingsheng Long, Jianmin Wang, Guiguang Ding, Jiaguang Sun, and Philip S. Yu. Transfer feature learning with joint distribution adaptation. In ICCV, 2013.
[112] Mingsheng Long, Yue Cao, Jianmin Wang, and Michael I. Jordan. Learning transferable features with deep adaptation networks. In ICML, 2015.
[113] Mingsheng Long, Jianmin Wang, and Michael I. Jordan. Unsupervised domain adaptation with residual transfer networks. In NeurIPS, 2016.
[114] Mingsheng Long, Han Zhu, Jianmin Wang, and Michael I Jordan. Deep transfer learning with joint adaptation networks. In ICML, 2017.
[115] Mingsheng Long, Zhangjie Cao, Jianmin Wang, and Michael I. Jordan. Conditional adversarial domain adaptation. In NeurIPS, 2018.
[116] Mingsheng Long, Yue Cao, Zhangjie Cao, Jianmin Wang, and Michael I. Jordan. Transferable representation learning with deep adaptation networks. TPAMI, 41(12):3071–3085, 2019.
[117] Christos Louizos, Max Welling, and Diederik P. Kingma. Learning sparse neural networks through l 0 regularization. In ICLR, 2018.
[118] Dhruv Mahajan, Ross Girshick, Vignesh Ramanathan, Kaiming He, Manohar Paluri, Yixuan Li, Ashwin Bharambe, and Laurens van der Maaten. Exploring the limits of weakly supervised pretraining. In ECCV, 2018.
[119] Arun Mallya and Svetlana Lazebnik. Piggyback: Adding multiple tasks to a single, fixed network by learning to mask. In ECCV, 2018.
[120] Yishay Mansour, Mehryar Mohri, and Afshin Rostamizadeh. Domain adaptation: Learning bounds and algorithms. In COLT, 2009.
[121] Tsendsuren Munkhdalai and Hong Yu. Meta networks. In ICML, 2017.
[122] Jiquan Ngiam, Daiyi Peng, Vijay Vasudevan, Simon Kornblith, Quoc V Le, and Ruoming Pang. Domain adaptive transfer learning with specialist models. arXiv preprint arXiv:1811.07056, 2018.
[123] Cuong Nguyen, Tal Hassner, Matthias Seeger, and Cedric Archambeau. Leep: A new measure to evaluate transferability of learned representations. In ICML, 2020.
[124] Aaron van den Oord, Yazhe Li, and Oriol Vinyals. Representation learning with contrastive predictive coding. NeurIPS, 2019.
[125] Sinno Jialin Pan and Qiang Yang. A survey on transfer learning. TKDE, pages 1345–1359, 2010.
[126] Sinno Jialin Pan, Ivor W. Tsang, James T. Kwok, and Qiang Yang. Domain adaptation via transfer component analysis. TNNLS, pages 199–210, 2011.
[127] Adam Paszke, Sam Gross, Francisco Massa, Adam Lerer, James Bradbury, Gregory Chanan, Trevor Killeen, Zeming Lin, Natalia Gimelshein, Luca Antiga, Alban Desmaison, Andreas Kopf, Edward Yang, Zachary DeVito, Martin Raison, Alykhan Tejani, Sasank Chilamkurthy, Benoit Steiner, Lu Fang, Junjie Bai, and Soumith Chintala. Pytorch: An imperative style, high-performance deep learning library. In NeurIPS, 2019.
[128] Xingchao Peng, Qinxun Bai, Xide Xia, Zijun Huang, Kate Saenko, and Bo Wang. Moment matching for multi-source domain adaptation. In ICCV, 2019.
[129] Jonas Peters, Peter B¨uhlmann, and Nicolai Meinshausen. Causal inference by using invariant prediction: identification and confidence intervals. Journal of the Royal Statistical Society. Series B (Statistical Methodology), pages 947–1012, 2016.
[130] Jonas Peters, Dominik Janzing, and Bernhard Sch¨olkopf. Elements of causal inference: foundations and learning algorithms. The MIT Press, 2017.
[131] Matthew E Peters, Mark Neumann, Mohit Iyyer, Matt Gardner, Christopher Clark, Kenton Lee, and Luke Zettlemoyer. Deep contextualized word representations. In NAACL, 2018.
[132] Telmo Pires, Eva Schlinger, and Dan Garrette. How multilingual is multilingual bert? In ACL, 2019.
[133] J. Quionero-Candela, M. Sugiyama, A. Schwaighofer, and N. D. Lawrence. Dataset shift in machine learning. The MIT Press, 2009.
[134] Alec Radford, Karthik Narasimhan, Tim Salimans, and Ilya Sutskever. Improving language understanding by generative pre-training. Technical report, OpenAI, 2018.
[135] Alec Radford, Jong Wook Kim, Chris Hallacy, Aditya Ramesh, Gabriel Goh, Sandhini Agarwal, Girish Sastry, Amanda Askell, Pamela Mishkin, Jack Clark, et al. Learning transferable visual models from natural language supervision. In ICML, 2021.
[136] Colin Raffel, Noam Shazeer, Adam Roberts, Katherine Lee, Sharan Narang, Michael Matena, Yanqi Zhou, Wei Li, and Peter J Liu. Exploring the limits of transfer learning with a unified text-to-text transformer. JMLR, 21(140):1–67, 2020.
[137] Aniruddh Raghu, Maithra Raghu, Samy Bengio, and Oriol Vinyals. Rapid learning or feature reuse? towards understanding the effectiveness of maml. In ICLR, 2020.
[138] Maithra Raghu, Chiyuan Zhang, Jon Kleinberg, and Samy Bengio. Transfusion: Understanding transfer learning for medical imaging. In NeurIPS, 2019.
[139] S-A Rebuffi, H. Bilen, and A. Vedaldi. Learning multiple visual domains with residual adapters. In NeurIPS, 2017.
[140] Ievgen Redko, Emilie Morvant, Amaury Habrard, Marc Sebban, and Youn`es Bennani. A survey on domain adaptation theory: learning bounds and theoretical guarantees, 2020.
[141] Shaoqing Ren, Kaiming He, Ross Girshick, and Jian Sun. Faster r-cnn: Towards real-time object detection with region proposal networks. In NeurIPS, 2015.
[142] Michael T. Rosenstein. To transfer or not to transfer. In NeurIPS, 2005.
[143] Evgenia. Rusak, Steffen Schneider, Peter Gehler, Oliver Bringmann, Wieland Brendel, and Matthias Bethge. Adapting imagenet-scale models to complex distribution shifts with self-learning. arXiv preprint arXiv:2104.12928, 2021.
[144] Olga Russakovsky, Jia Deng, Hao Su, Jonathan Krause, Sanjeev Satheesh, Sean Ma, Zhiheng Huang, Andrej Karpathy, Aditya Khosla, Michael Bernstein, Alexander C. Berg, and Li Fei-Fei. ImageNet Large Scale Visual Recognition Challenge. IJCV, 115(3):211– 252, 2015.
[145] Andrei A Rusu, Dushyant Rao, Jakub Sygnowski, Oriol Vinyals, Razvan Pascanu, Simon Osindero, and Raia Hadsell. Meta-learning with latent embedding optimization. In ICLR, 2019.
[146] Kuniaki Saito, Kohei Watanabe, Yoshitaka Ushiku, and Tatsuya Harada. Maximum classifier discrepancy for unsupervised domain adaptation. In CVPR, 2018.
[147] Kuniaki Saito, Yoshitaka Ushiku, Tatsuya Harada, and Kate Saenko. Strong-weak distribution alignment for adaptive object detection. In CVPR, 2019.
[148] Hadi Salman, Andrew Ilyas, Logan Engstrom, Ashish Kapoor, and Aleksander Madry. Do adversarially robust imagenet models transfer better? In NeurIPS, 2020.
[149] Swami Sankaranarayanan, Yogesh Balaji, Carlos D. Castillo, and Rama Chellappa. Generate to adapt: Aligning domains using generative adversarial networks. In CVPR, 2018.
[150] Adam Santoro, Sergey Bartunov, Matthew Botvinick, Daan Wierstra, and Timothy Lillicrap. Meta-learning with memory-augmented neural networks. In ICML, 2016.
[151] Timo Schick and Hinrich Sch¨utze. Exploiting cloze questions for few-shot text classification and natural language inference. In EACL, 2020.
[152] J¨urgen Schmidhuber. Evolutionary principles in self-referential learning. PhD thesis, Technische Universit¨at M¨unchen, 1987.
[153] Bernhard Sch¨olkopf, Dominik Janzing, Jonas Peters, Eleni Sgouritsa, Kun Zhang, and Joris Mooij. On causal and anticausal learning. In ICML, 2012.
[154] Bernhard Sch¨olkopf, Francesco Locatello, Stefan Bauer, Nan Rosemary Ke, Nal Kalchbrenner, Anirudh Goyal, and Yoshua Bengio. Toward causal representation learning. Proceedings of the IEEE, 109(5):612–634, 2021.
[155] Andrew W Senior, Richard Evans, John Jumper, James Kirkpatrick, Laurent Sifre, Tim Green, Chongli Qin, Augustin ˇZ´ıdek, Alexander WR Nelson, Alex Bridgland, et al. Improved protein structure prediction using potentials from deep learning. Nature, 577 (7792):706–710, 2020.
[156] Pierre Sermanet, David Eigen, Xiang Zhang, Micha¨el Mathieu, Rob Fergus, and Yann LeCun. Overfeat: Integrated recognition, localization and detection using convolutional networks. arXiv preprint arXiv:1312.6229, 2013.
[157] Ashish Shrivastava, Tomas Pfister, Oncel Tuzel, Josh Susskind, Wenda Wang, and Russell Webb. Learning from simulated and unsupervised images through adversarial training. In CVPR, 2017.
[158] Rui Shu, Hung H. Bui, Hirokazu Narui, and Stefano Ermon. A dirt-t approach to unsupervised domain adaptation. In ICLR, 2018.
[159] Yang Shu, Zhangjie Cao, Jinghan Gao, Jianmin Wang, and Mingsheng Long. Omni-training for data-efficient deep learning. arXiv preprint arXiv:2110.07510, 2021a.
[160] Yang Shu, Zhi Kou, Zhangjie Cao, Jianmin Wang, and Mingsheng Long. Zoo-tuning: Adaptive transfer from a zoo of models. In ICML, 2021b.
[161] David Silver, Aja Huang, Chris J Maddison, Arthur Guez, Laurent Sifre, George Van Den Driessche, Julian Schrittwieser, Ioannis Antonoglou, Veda Panneershelvam, Marc Lanctot, et al. Mastering the game of go with deep neural networks and tree search. Nature, 529(7587):484–489, 2016.
[162] Jake Snell, Kevin Swersky, and Richard S. Zemel. Prototypical networks for few-shot learning. In NeurIPS, 2017.
[163] Bharath K. Sriperumbudur, Arthur Gretton, Kenji Fukumizu, Bernhard Sch¨olkopf, and Gert R. G. Lanckriet. Hilbert space embeddings and metrics on probability measures. JMLR, 2010.
[164] Masashi Sugiyama, Matthias Krauledat, and Klaus-Robert M¨uller. Covariate shift adaptation by importance weighted cross validation. JMLR, 8(35):985–1005, 2007.
[165] Masashi Sugiyama, Shinichi Nakajima, Hisashi Kashima, Paul Buenau, and Motoaki Kawanabe. Direct importance estimation with model selection and its application to covariate shift adaptation. In NeurIPS, 2008.
[166] Baochen Sun and Kate Saenko. Deep coral: Correlation alignment for deep domain adaptation. In ECCV, 2016.
[167] Qianru Sun, Yaoyao Liu, Tat-Seng Chua, and Bernt Schiele. Meta-transfer learning for few-shot learning. In CVPR, 2019a.
[168] Yu Sun, Shuohuan Wang, Yukun Li, Shikun Feng, Xuyi Chen, Han Zhang, Xin Tian, Danxiang Zhu, Hao Tian, and Hua Wu. Ernie: Enhanced representation through knowledge integration. arXiv preprint arXiv:1904.09223, 2019b.
[169] Yaniv Taigman, Adam Polyak, and Lior Wolf. Unsupervised cross-domain image generation. In ICLR, 2017.
[170] Sebastian Thrun and Lorien Pratt. Learning to learn. Springer Science & Business Media, 1998.
[171] Yonglong Tian, Dilip Krishnan, and Phillip Isola. Contrastive multiview coding. In ECCV, 2020.
[172] Lisa Torrey and Jude Shavlik. Transfer learning. 2010.
[173] Yi-Hsuan Tsai, Wei-Chih Hung, Samuel Schulter, Kihyuk Sohn, Ming-Hsuan Yang, and Manmohan Chandraker. Learning to adapt structured output space for semantic segmentation. In CVPR, 2018.
[174] Eric Tzeng, Judy Hoffman, Ning Zhang, Kate Saenko, and Trevor Darrell. Deep domain confusion: Maximizing for domain invariance. 2014.
[175] Eric Tzeng, Judy Hoffman, Trevor Darrell, and Kate Saenko. Simultaneous deep transfer across domains and tasks. In ICCV, pages 4068–4076, 2015.
[176] Eric Tzeng, Judy Hoffman, Kate Saenko, and Trevor Darrell. Adversarial discriminative domain adaptation. In CVPR, 2017.
[177] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, �Lukasz Kaiser, and Illia Polosukhin. Attention is all you need. In NeurIPS, 2017.
[178] Petar Veliˇckovi´c, William Fedus, William L Hamilton, Pietro Li`o, Yoshua Bengio, and R Devon Hjelm. Deep graph infomax. In ICLR, 2019.
[179] Pascal Vincent, Hugo Larochelle, Yoshua Bengio, and Pierre-Antoine Manzagol. Extracting and composing robust features with denoising autoencoders. In ICML, 2008.
[180] Oriol Vinyals, Charles Blundell, Timothy Lillicrap, Daan Wierstra, et al. Matching networks for one shot learning. In NeurIPS, 2016.
[181] Oriol Vinyals, Igor Babuschkin, Wojciech M Czarnecki, Micha¨el Mathieu, Andrew Dudzik, Junyoung Chung, David H Choi, Richard Powell, Timo Ewalds, Petko Georgiev, et al. Grandmaster level in starcraft ii using multi-agent reinforcement learning. Nature, 575 (7782):350–354, 2019.
[182] Tuan-Hung Vu, Himalaya Jain, Maxime Bucher, Matthieu Cord, and Patrick Perez. Advent: Adversarial entropy minimization for domain adaptation in semantic segmentation. In CVPR, 2019.
[183] Alex Wang, Amanpreet Singh, Julian Michael, Felix Hill, Omer Levy, and Samuel R. Bowman. GLUE: A multi-task benchmark and analysis platform for natural language understanding. In ICLR, 2019a.
[184] Haohan Wang, Songwei Ge, Zachary Lipton, and Eric P Xing. Learning robust global representations by penalizing local predictive power. In NeurIPS, 2019b.
[185] Ximei Wang, Ying Jin, Mingsheng Long, Jianmin Wang, and Michael I Jordan. Transferable normalization: Towards improving transferability of deep neural networks. In NeurIPS, 2019c.
[186] Ximei Wang, Jinghan Gao, Mingsheng Long, and Jianmin Wang. Self-tuning for dataefficient deep learning. In ICML, 2021.
[187] Zirui Wang, Zihang Dai, Barnab´as P´oczos, and Jaime G. Carbonell. Characterizing and avoiding negative transfer. In CVPR, 2019d.
[188] Jason Wei, Maarten Bosma, Vincent Y. Zhao, Kelvin Guu, Adams Wei Yu, Brian Lester, Nan Du, Andrew M. Dai, and Quoc V. Le. Finetuned language models are zero-shot learners. In ICLR, 2022.
[189] Longhui Wei, Shiliang Zhang, Wen Gao, and Qi Tian. Person transfer gan to bridge domain gap for person re-identification. In CVPR, 2018.
[190] Ross Wightman. Pytorch image models. https://github.com/rwightman/ pytorch-image-models, 2019.
[191] Yuxin Wu and Kaiming He. Group normalization. In ECCV, 2018.
[192] Zhirong Wu, Yuanjun Xiong, X Yu Stella, and Dahua Lin. Unsupervised feature learning via non-parametric instance discrimination. In CVPR, 2018.
[193] Runxin Xu, Fuli Luo, Zhiyuan Zhang, Chuanqi Tan, Baobao Chang, Songfang Huang, and Fei Huang. Raise a child in large language model: Towards effective and generalizable fine-tuning. In EMNLP, 2021.
[194] I Zeki Yalniz, Herv´e J´egou, Kan Chen, Manohar Paluri, and Dhruv Mahajan. Billion-scale semi-supervised learning for image classification. arXiv preprint arXiv:1905.00546, 2019.
[195] Zhilin Yang, Zihang Dai, Yiming Yang, Jaime Carbonell, Russ R Salakhutdinov, and Quoc V Le. Xlnet: Generalized autoregressive pretraining for language understanding. In NeurIPS, 2019.
[196] Huaxiu Yao, Ying Wei, Junzhou Huang, and Zhenhui Li. Hierarchically structured metalearning. In ICML, 2019.
[197] Jason Yosinski, Jeff Clune, Yoshua Bengio, and Hod Lipson. How transferable are features in deep neural networks? In NeurIPS, 2014.
[198] Kaichao You, Yong Liu, Jianmin Wang, and Mingsheng Long. Logme: Practical assessment of pre-trained models for transfer learning. In ICML, 2021.
[199] Amir Roshan Zamir, Alexander Sax, William B. Shen, Leonidas J. Guibas, Jitendra Malik, and Silvio Savarese. Taskonomy: Disentangling task transfer learning. In CVPR, 2018.
[200] Werner Zellinger, Thomas Grubinger, Edwin Lughofer, Thomas Natschl¨ager, and Susanne Saminger-Platz. Central moment discrepancy (cmd) for domain-invariant representation learning. In ICLR, 2017.
[201] Chiyuan Zhang, Samy Bengio, Moritz Hardt, Benjamin Recht, and Oriol Vinyals. Understanding deep learning requires rethinking generalization. In ICLR, 2017.
[202] Hongyang Zhang, Yaodong Yu, Jiantao Jiao, Eric P. Xing, Laurent El Ghaoui, and Michael I. Jordan. Theoretically principled trade-off between robustness and accuracy. In ICML, 2019a.
[203] Jeffrey O. Zhang, Alexander Sax, Amir Zamir, Leonidas J. Guibas, and Jitendra Malik. Side-tuning: Network adaptation via additive side networks. 2019b.
[204] Yuchen Zhang, Tianle Liu, Mingsheng Long, and Michael Jordan. Bridging theory and algorithm for domain adaptation. In ICML, 2019c.
[205] Zhilu Zhang and Mert R. Sabuncu. Generalized cross entropy loss for training deep neural networks with noisy labels. In NeurIPS, 2018.
[206] Nanxuan Zhao, Zhirong Wu, Rynson W. H. Lau, and Stephen Lin. What makes instance discrimination good for transfer learning? In ICLR, 2021.
[207] Lucia Zheng, Neel Guha, Brandon R. Anderson, Peter Henderson, and Daniel E. Ho. When does pretraining help? assessing self-supervised learning for law and the casehold dataset. In ICAIL, 2021.
[208] Jincheng Zhong, Ximei Wang, Zhi Kou, Jianmin Wang, and Mingsheng Long. Bi-tuning of pre-trained representations. arXiv preprint arXiv:2011.06182, 2020.
[209] Jun-Yan Zhu, Taesung Park, Phillip Isola, and Alexei A Efros. Unpaired image-to-image translation using cycle-consistent adversarial networks. In ICCV, 2017.
[210] Yukun Zhu, Ryan Kiros, Rich Zemel, Ruslan Salakhutdinov, Raquel Urtasun, Antonio Torralba, and Sanja Fidler. Aligning books and movies: Towards story-like visual explanations by watching movies and reading books. In ICCV, 2015.
[211] Fuzhen Zhuang, Zhiyuan Qi, Keyu Duan, Dongbo Xi, Yongchun Zhu, Hengshu Zhu, Hui Xiong, and Qing He. A comprehensive survey on transfer learning. Proceedings of the IEEE, 109(1):43–76, 2021.
[212] Yang Zou, Zhiding Yu, B. V. K. Vijaya Kumar, and Jinsong Wang. Unsupervised domain adaptation for semantic segmentation via class-balanced self-training. In ECCV, 2018.