GELU激活函数
论文:GAUSSIAN ERROR LINEAR UNITS (GELUS)
年份:2016
ReLU激活函数的公式可以理解为:
R
e
L
U
(
x
)
=
x
⋅
{
1
,
x
≥
,
x
<
ReLU(x) = x\cdot \begin{cases} 1,&x\ge 0\\ 0,&x<0 \end{cases}
ReLU(x)=x⋅{1,0,x≥0x<0
ReLU、Dropout等机制都希望将\textbf{不重要}的激活信息规整为零。也就是对于输入的值,根据它需要的情况乘以1或0,需要乘以谁不像ReLU人工定义,而是根输入有关。更为数学的描述,对于一个输入
x
∼
N
(
,
1
)
x\sim N(0, 1)
x∼N(0,1),即
x
x
x服从标准正态分布,而输入
x
x
x还要乘上一个伯努利分布
B
e
r
n
o
u
l
l
i
(
Φ
(
x
)
)
Bernoulli(\Phi(x))
Bernoulli(Φ(x))。
随着
x
x
x的降低,输出值被归为0的概率就会升高。对于ReLU,这个界限就是0,输入小于0时,输出就归为0。
则怎么判断这个伯努利试验到底失败还是成功呢?则在引入
Φ
(
x
)
\Phi(x)
Φ(x)来控制伯努利试验成功的概率即:
Φ
(
x
)
⋅
I
x
+
(
1
−
Φ
(
x
)
)
⋅
x
=
x
⋅
Φ
(
x
)
\Phi(x)\cdot Ix + (1-\Phi(x))\cdot 0x=x\cdot \Phi(x)
Φ(x)⋅Ix+(1−Φ(x))⋅0x=x⋅Φ(x)
这个表达式表示根据
x
x
x比其它输入大多少来缩放它。由于高斯分布的累积分布函数通常用误差函数来计算,因此将高斯误差线性单元)(GELU)定义为:
G
E
L
U
(
x
)
=
x
Φ
(
x
)
=
x
⋅
1
2
(
1
+
e
r
f
(
x
/
2
)
)
GELU(x) = x\Phi(x) = x\cdot \frac{1}{2}(1+erf(x/\sqrt{2}))
GELU(x)=xΦ(x)=x⋅21(1+erf(x/2))
近似于
G
E
L
U
(
x
)
≈
0.5
x
(
1
+
t
a
n
h
(
2
/
π
(
x
+
0.044715
x
3
)
)
)
≈
x
⋅
s
i
g
m
o
i
d
(
1.702
x
)
GELU(x) \approx 0.5x(1+tanh(\sqrt{2/\pi}(x+0.044715x^3)))\approx x\cdot sigmoid(1.702x)
GELU(x)≈0.5x(1+tanh(2/π(x+0.044715x3)))≈x⋅sigmoid(1.702x)
当
μ
=
,
σ
=
1
\mu = 0,\sigma=1
μ=0,σ=1时,将GELU称为Sigmoid Linear Unit(SiLU)激活函数。
GELU激活函数的曲线和导数曲线如下图所示。
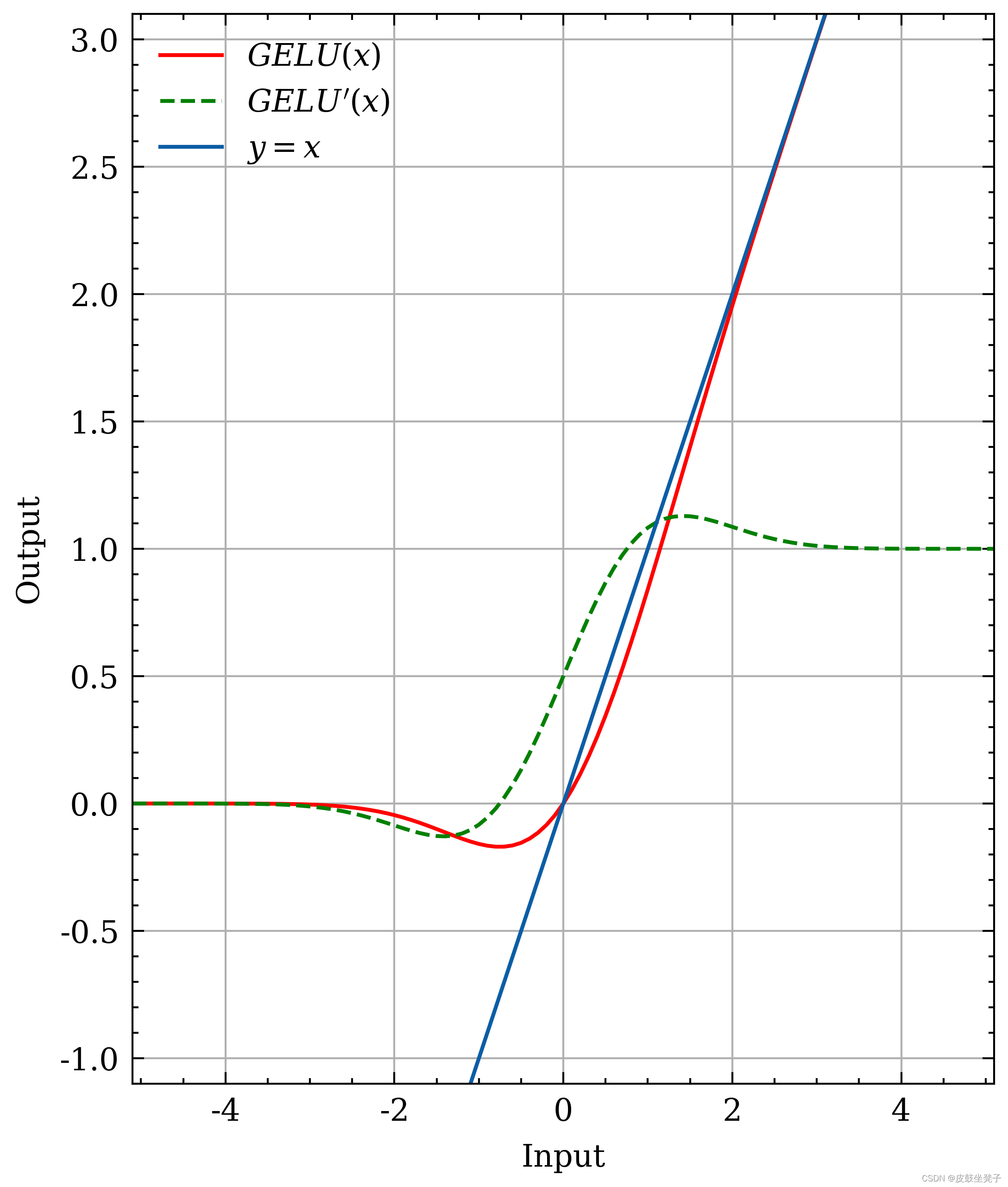
- GELU为非单调激活函数,有助于保持小的负值,从而稳定网络梯度流;
- GELU在0附近接近与恒等函数
x
x
x。 - GELU的最小值为-0.21,值域为
[
−
0.21
,
+
∞
]
[-0.21, +\infty]
[−0.21,+∞]。上界是任何激活函数都需要的特征,因为这样可以避免导致训练速度急剧下降的梯度饱和,因此加快训练过程。无下界有助于实现强正则化效果; - GELU的梯度不容易造成梯度爆炸和梯度消失。
- 光滑性:光滑的激活函数有较好的泛化能力和稳定的优化能力,可以提高模型的性能