LeetCode-45. 跳跃游戏II - 题解分析

题目来源

45. 跳跃游戏 II

题目详情

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

• 0 <= j <= nums[i]
• i + j < n

返回到达nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置，跳1步，然后跳3步到达数组的最后一个位置。

示例 2:

输入: nums = [2,3,0,1,4]
输出: 2

提示:

• 1 <= nums.length <= 104
• 0 <= nums[i] <= 1000
• 题目保证可以到达nums[n-1]

相似题目

55. 跳跃游戏

题解分析

本题与[55. 跳跃游戏]这题不同，不能使用相同的贪心思路来解决。这里需要求解的问题是最小的跳跃次数，而要求解最小的跳跃次数需要每次在跳跃时选择尽可能跨度大的格子。

换句话说，只需要判断哪一个选择最具有「潜力」即可：

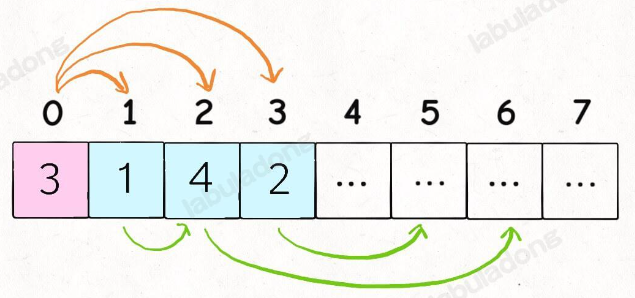
比如上图这种情况，我们站在索引 0 的位置，可以向前跳 1，2 或 3 步，你说应该选择跳多少呢？

显然应该跳 2 步调到索引 2，因为 nums[2] 的可跳跃区域涵盖了索引区间 [3..6]，比其他的都大。如果想求最少的跳跃次数，那么往索引 2 跳必然是最优的选择。

你看，这就是贪心选择性质，我们不需要「递归地」计算出所有选择的具体结果然后比较求最值，而只需要做出那个最有「潜力」，看起来最优的选择即可。

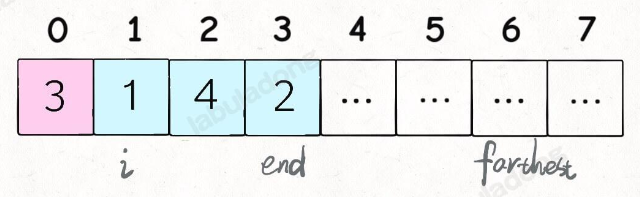
i 和 end 标记了可以选择的跳跃步数，farthest 标记了所有选择 [i..end] 中能够跳到的最远距离，jumps 记录了跳跃次数。

本算法的时间复杂度 O(N)，空间复杂度 O(1)。

java实现

class Solution {
    public int jump(int[] nums) {
        int right = 0, maxStep = 0, len = nums.length;
        int steps = 0;
        for (int i=0; i<len-1; i++) {
            maxStep = Math.max(maxStep, nums[i] + i);
            if (i == right) {
                right = maxStep;
                steps++;
            }
        }
        return steps;
    }
}

参考

如何运用贪心思想玩跳跃游戏