先来介绍一下时间复杂度:
同一问题可用不同算法解决,而一个算法的质量优劣将影响到算法乃至程序的效率。算法分析的目的在于选择合适算法和改进算法。
计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。这是一个关于代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,它考察当输入值大小趋近无穷时的情况。
时间复杂度的优化通常在暴力枚举中尤为重要,或许O(n*n)会得零分但是O(n*logn)可以得满分,所以在编写程序过程中我们要优先考虑时间较短的算法(洛谷里最绝望的就是看到TLE,这意味着代码要重新编写)。总之有快方法用上绝对没问题,除非NOIP时间不够可以快速写一段骗(拿)一些分数。
下面以洛谷P2241 统计方形(数据加强版)为例讲解一下具体如何不断优化程序的时间复杂度:
例10.1 (洛谷 P2241, NOIP1997 普及组 加强)
有一个 n×m(n, m ≤ 5000) 的棋盘,求其方格包含多少个(四边平 行于坐标轴的)正方形和长方形。
本题中, 长方形中不包括正方形。
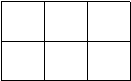
样例解释: 如图,正方形一共 8 个,长方形 10 个 正方形中,边长为 1 的 6 个,边长为 2 的 2 个;
长方形中, 1 ×2 的 4 个, 1 ×3 的 2 个, 2 × 1 的 3 个, 2 ×3 的 1个。
思路1:用四重循环,直接枚举 4 个参数,即两横边两竖边:
通过左上角和右下角的顶点进行枚举,如果长度相等就是正方形,否则就是长方形。
所以,这样可以保证不重复地遍历所有的方形。
根据循环的范围可知,我们也没有遗漏任何的方形。
时间复杂度O(n2 m2 ) ……似乎有点慢。
但是至少, 答案正确了。
1 //枚举左上、右下顶点 时间复杂度O(n^2*m^2) 2 #include<bits/stdc++.h> 3 using namespace std; 4 typedef long long LL; //LL是已经定义好的long long 5 int main(){ 6 int n,m; 7 LL squ=0,rec=0;//squ统计正方形个数,rec统计长方形个数 8 cin>>n>>m; 9 for(int x1=0;x1<n;x1++) 10 for(int y1=0;y1<m;y1++) 11 for(int x2=x1+1;x2<=n;x2++) 12 for(int y2=y1+1;y2<=m;y2++) //四层循环不TLE才怪 13 if (x2-x1 == y2-y1)squ++; 14 else rec++; 15 cout<<squ<<" "<<rec<<endl; 16 return 0; 17 }
为什么是 x2 从 x1+1 开始, y2 从 y1+1 开始枚举?
• 如果 x1 > x2, 那么 x1 就不再是左侧了, x2 才是左侧 (左图)
• 如果 x1 = x2, 那么无法构成长方形, 退化为一根线段 (中图)(就是那根消失的线段)
• 只有 x1 < x2, 才能正常构成长方形(右图)。
y1 、y2 同理
思路 2: 以下左图中的点 (3, 4)为例(左下角为原点)。
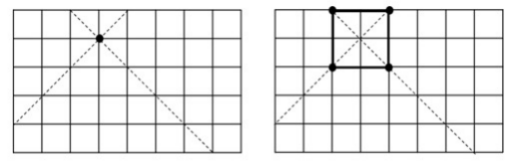
位于同一对角线 (图中虚线)上所有点均可构成正方形。
除自身所在行列外,所有其它点均可与其构成长方形;故直接得 长方形数为 nm – 正方形数。
从右图可以看出, 每一个长/正方形均被其 4 个顶点各计算一次。 因此,最终答案需要除以 4。
斜线上的格点个数为多少呢?
若顶点在长方形顶点,格点个数为长方形的短边长,即 min(n,m)。
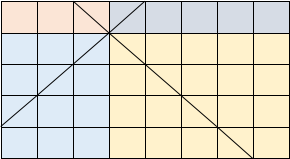
否则,以顶点为界分为4份 。
每份都这样计算,得到正方形个数: min x, y + min n − x, y + min x, m − y + min(n − x, m − y)
因此, 枚举(x, y)后,可在 O(1) 时间内计算答案,求和。 总时间复杂度 O(nm),直接优化掉一个 O(nm)
1 //枚举一个点构成的所有矩形,统计结果除4 时间复杂度O(n*m) 2 #include<bits/stdc++.h> 3 using namespace std; 4 typedef long long LL; //LL是已经定义好的long long 5 int main(){ 6 int n,m; 7 LL squ=0,rec=0; 8 cin>>n>>m; 9 for(int x=0;x<=n;x++) 10 for(int y=0;y<=m;y++){ 11 LL tmp=min(x,y)+min(n-x,y)+min(x,m-y)+min(n-x,m-y);//对角线的正方形枚举方式 12 squ+=tmp; 13 rec+=n*m-tmp; 14 } 15 cout<<squ/4<<" "<<rec/4<<endl;//四个顶点算了四次,所以要除4输出 16 return 0; 17 }
还能不能更快呢?
思路 3:每一个长方形重复了4次。能否不重复呢?
结合思路 1可知, 只需考虑右上角为 (x, y) 的情况,因此计算斜线 上的顶点时, 只需要向左下角一个方向拓展!
(先算 4 个方向, 再除以 4,可谓是画蛇添足啊…… )
1 //枚举右下角顶点 时间复杂度O(n*m) 2 #include<bits/stdc++.h> 3 using namespace std; 4 typedef long long LL; 5 int main(){ 6 int n,m; 7 LL squ=0,rec=0; 8 cin>>n>>m; 9 for(int x=0;x<=n;x++) 10 for(int y=0;y<=m;y++){ 11 LL tmp=min(x,y); 12 squ+=tmp; 13 rec+=x*y-tmp; 14 } 15 cout<<squ<<" "<<rec<<endl; 16 return 0; 17 }
当然,这里选择固定其它角也是等价的,但是固定右上角最简单。
注意:这里的原点是在左下角, 列是 x,行是 y。
如果选择左上角 作为原点, 那么枚举的就是长方形右下角。
思路4:枚举边长 (a, b)。题目变为在 n × m 的长方形中能放置多少 个 a×b 的方形。
注意 a 、b 有序, a×b 和 b×a 不等价。
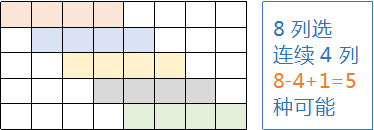
• n 列中选连续 a 列:[1,a],[2,a+1], … ,[n-a+1,n],共 n-a+1 种可能。
• m 行中选连续 b 行构成方形, 同理有 m-b+1 种情况。 所以 n × m 的长方形中可容纳 (n-a+1)×(m-b+1) 个 a×b 的矩形。
对于边长 k, 只有长等于宽, 才能构成正方形;其余均为长方形。
如果 a=b, 就计入正方形。 使用循环枚举 a 、b, 累加求和即可
1 //枚举两条边 时间复杂度O(n*m) 2 #include<bits/stdc++.h> 3 using namespace std; 4 typedef long long LL; 5 int main(){ 6 int n,m; 7 LL squ=0,rec=0; 8 cin>>n>>m; 9 for(int a=1;a<=n;a++) 10 for(int b=1;b<=m;b++) 11 if(a==b) 12 squ+=(n-a+1)*(m-b+1); 13 else 14 rec+=(n-a+1)*(m-b+1); 15 cout<<squ<<" "<<rec<<endl; 16 return 0; 17 }
还可以再快!!!
思路 5:沿用刚才乘法原理的思想,枚举量还可进一步减少?
在 n × m 的长方形中的矩形个数, 等价于在 m+1 条行线中选首尾 2 行、在 n+1 条列线中选首尾 2 列所围成的方形数目!


在 n+1 列中选 2 列线围长方形,左列 n+1 种情况 ;右线列不能和 左列线重复, 只有 n 种情况,将他们乘起来。
由于重复统计 (左右和右左),要除以2,有 1/2n(n + 1) 种可能。 同理,行有 1/2m(m + 1) 种可能。一共1/4 m(m + 1) n (n+1)矩形。
借助思路4, 去掉其中的正方形。时间复杂度降到 O(min(m, n))。
1 //枚举一条边 时间复杂度:O(n) 2 #include<bits/stdc++.h> 3 using namespace std; 4 typedef long long LL; 5 int main(){ 6 int n,m; 7 LL squ=0,rec=0; 8 cin>>n>>m; 9 for(int a=1;a<=min(n,m);a++) 10 squ+=(n-a+1)*(m-a+1); 11 rec=(n+1)*n*(m+1)*m/4-squ; 12 cout<<squ<<" "<<rec<<endl; 13 return 0; 14 }