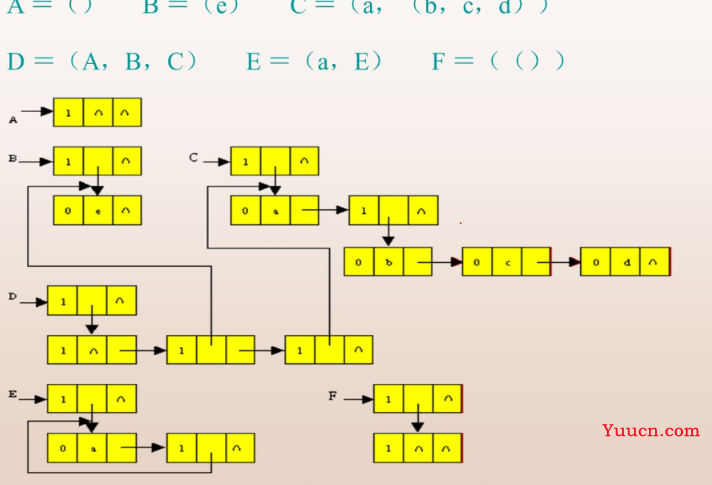
数据结构基础—数组和广义表
一、数组
1.数据的定义
数组类似于线性表,就是多维结构的顺序表,
2.稀疏数组
a.稀疏数组的定义:
假设m行n列的矩阵中含有t个非零元素若t/(m*n) <= 0.05,则称该矩阵为稀疏矩阵
稀疏矩阵也分为特殊矩阵和随机矩阵随机
- 特殊矩阵:三角,对角...
- 随机矩阵:非零元素随机出现
b.随机稀疏矩阵的压缩存储方式
- 三元组顺序表:
又称为双下标法,特点是有序存储,便于依次处理矩阵,随机性不够高
typedef struct{
int i,j;//非零的行下标和列下标
ElemType e;//非零的值
}Triple;//三元组
typedef union{
Triple data[MaxSize+1];//非零元素信息
int mu,nu,tu;//矩阵的行,列,和非零个数
}TSMatrix;//稀疏矩阵
小应用:如何求转置
利用三元组来实现
T.data[p].i = M.data[p].j;
T.data[p].j = M.data[p].i;
T.data[p].e = M.data[p].e;
问题,行列非零顺序不同(一个按行,一个按列放)
将原矩阵按列放
num原矩阵按列,转置矩阵按行做标记(有非零元,则该位置+1)
先全部置零,然后遍历所有非零元,让num[其列数]++,这样就记录了转置后矩阵每行非零元的个数
cpot:其初值值代表了,在转置矩阵的新行中首次出现的位置(,在该位置前已经有了所有非零原的位置(个数),即,该数就是新转置矩阵的第spot个元素),每次匹配完记得让其值++(原矩阵中某列可能含有多个元素,匹配完一个后数值要增加,仅仅对该行(列产生影响),后一行(列的数不受影响))
//已知 TSMatrix T;
//求转置
TSMatrix GetTran(){
TSMatrix M;//转置矩阵
M.mu = T.nu;
M.nu = T.mu;
M.tu = T.tu;
int col;
int num[MaxSize+1];
int cpot[MaxSize+1];
if(M.tu){
for(col = 1;col <= T.nu;col++) {
num[col] = 0; //先把数组置零
}
for(int t = 1;t <= T.tu;t++) {
num[T.data[t].j]++; //记录每一列非零元素个数 []中是列数,而数组的大小则是每列的个数(桶排序,标记)
}
cpot[1]=1;
//在转置矩阵的col行中首次出现的位置
for(col = 2;col <= T.nu;col++)
cpot[col] = cpot[col-1]+num[col-1];
//转置开始
for(int p = 1;p <= T.tu;p++){
col=T.data[p].j; //读取原三元组第p个元素的列
int q = cpot[col]; //q:p在转置矩阵的col行中非零首次出现的位置(次序)
M.data[q].i=T.data[p].j;
M.data[q].j=T.data[p].i;
M.data[q].e=T.data[p].e;
cpot[col]++;
}
}
return M;
}
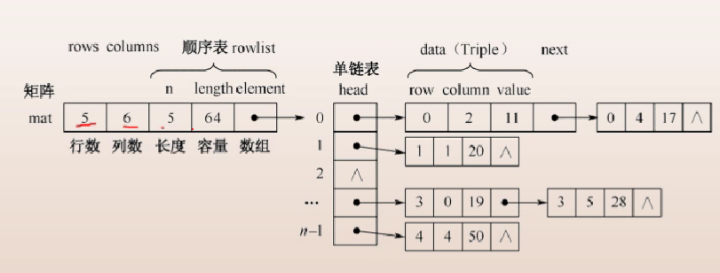
- 行逻辑联接的顺序表
typedef struct {
int i,j;//非零元的行列
int e;//元素大小
}triple;//三元组
typedef struct{
triple data[MaxSize+1];//非零信息
int rpos[MAXRC+1];//行每行首非零元的位置(就是该行第一个非零元素是第几个非零元和那个求转置时是一样的)
int mu, nu, tu;//行,列,个数
}RLSMatrix;// 行逻辑链接顺序表类型
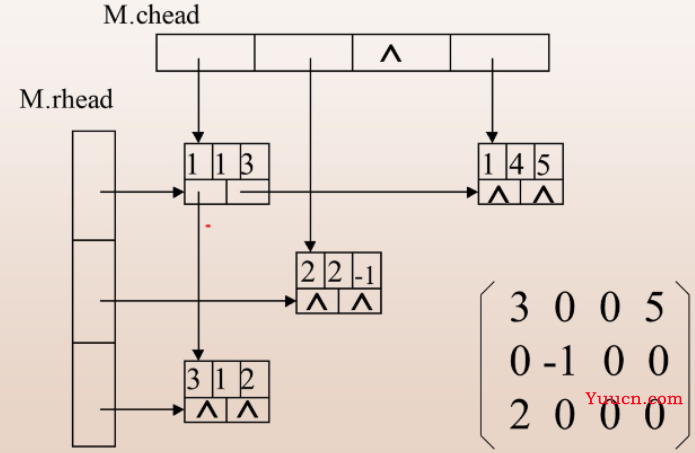
- 十字链表
typedef struct Lnode{
int row, col;
int element;
struct Lnode* right;
struct Lnode* down;
}Node, *LNode;
//十字链表
typedef struct { //十字链表
LNode* rowHead;
LNode* colHead;
int rows, cols, nzeroNums; //行数、列数、非0元素个数
}Cross, *LCross;
二、广义表:
1.广义表的定义
递归定义的线性结构
是一个集合:每一个元素要不是一个原子,要不就是一个广义表(递归)
-
有顺序:一一对应,和线性表不同,元素类型不同
-
线性表:特殊的广义表,深度为1(一个括弧一个深度)
原子的深度是0,一个get="_blank">括号一个深度(空表 S = ():长度0,深度为1,但是S1 = (S) =(())不是空表,深度为1)
2.性质:
-
递归定义的线性结构:两层含义:元素是一个另一个广义表,元素可以是本身
-
长度为最外层的元素个数
-
深度为括号数(括弧的重数) = max子表深度 +1(原子深度为零)
-
多层次的线性表,有相对次序
-
可以共享
-
任何一个非空表可以分为头尾表示
3.头尾表示
表头是第一个元素,表尾剩余所有元素组成的表(永远是表)

4.表示方法(存储)
- 头尾指针链表
每个节点:表结点,原子结点(共用体)
表结点:两个指针:头、尾
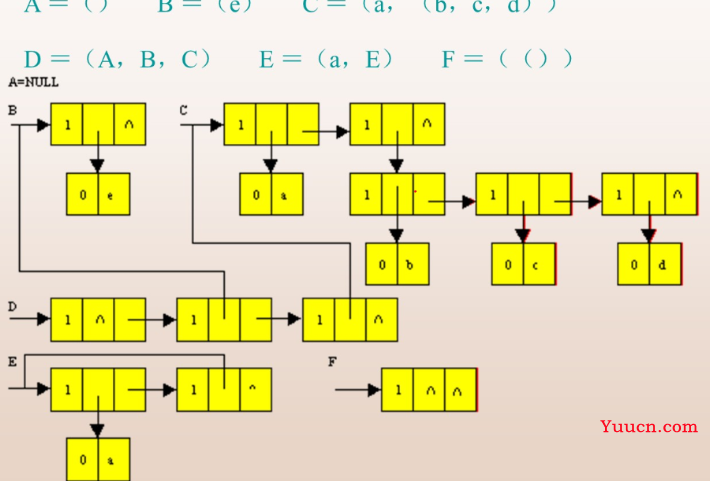
- 子表分析法(孩子兄弟分析法)