汉诺塔问题
在经典汉诺塔问题中,有 3 根柱子及 n 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。
请编写程序,用栈将所有盘子从第一根柱子移到最后一根柱子。
你需要原地修改栈。
输入:A = [2, 1, 0], B = [], C = []
输出:C = [2, 1, 0]
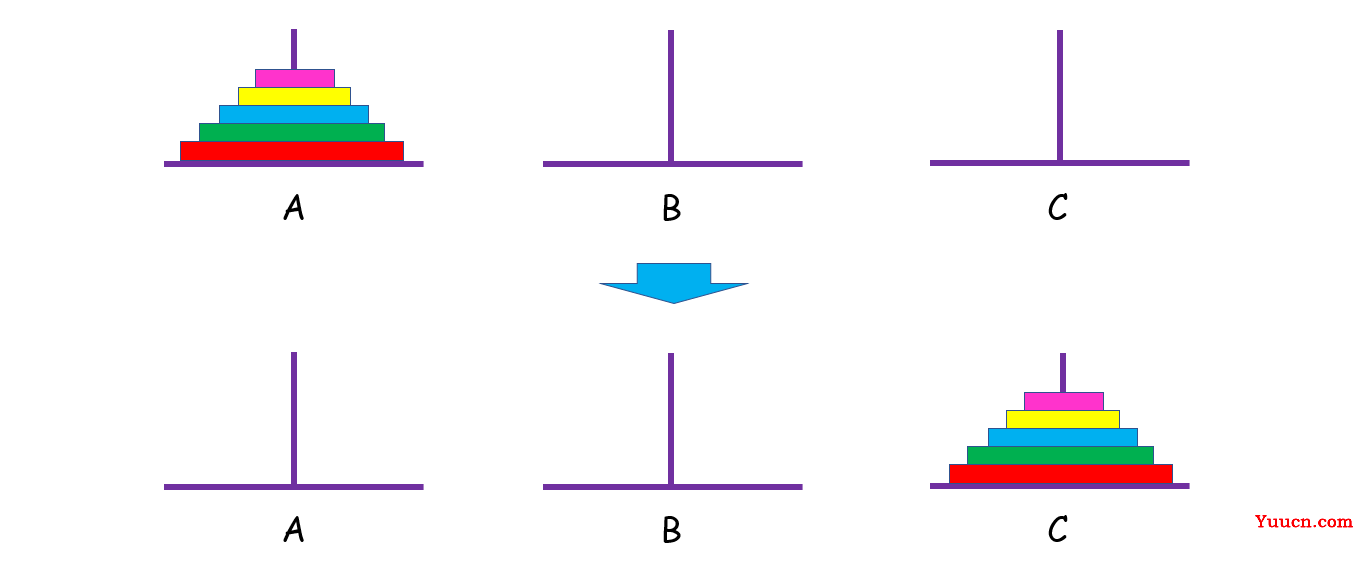
解题思路:递归与分治
这是一道递归方法的经典题目,乍一想还挺难理清头绪的,我们不妨先从简单的入手。
假设 n = 1,只有一个盘子,很简单,直接把它从 A 中拿出来,移到 C 上;
如果 n = 2 呢?这时候我们就要借助 B 了,因为小盘子必须时刻都在大盘子上面,共需要 4 步。
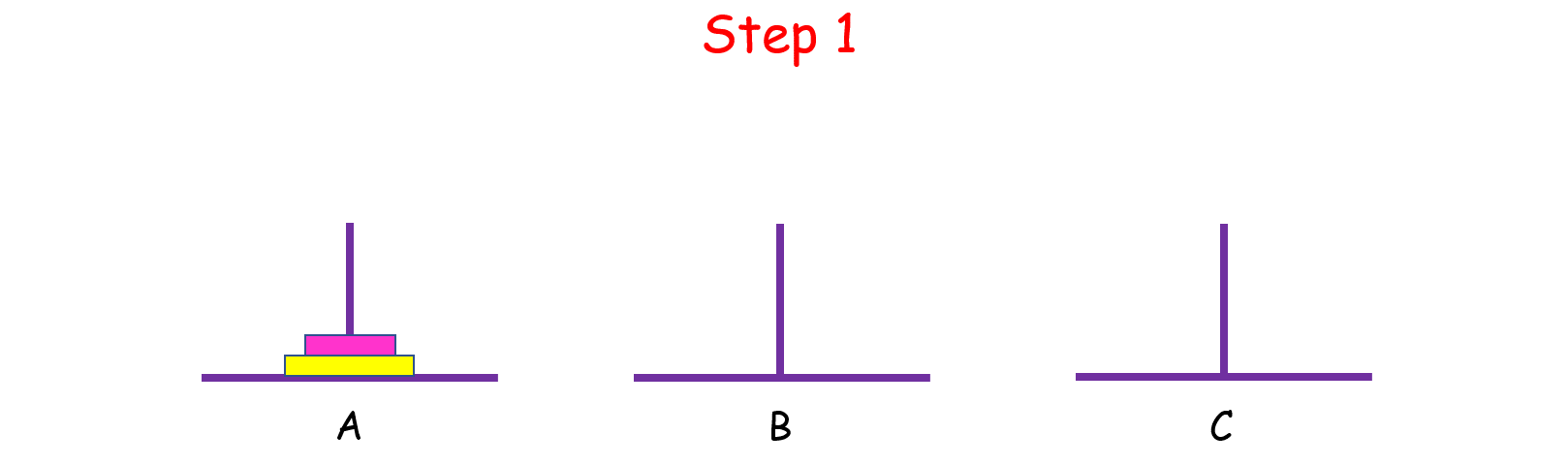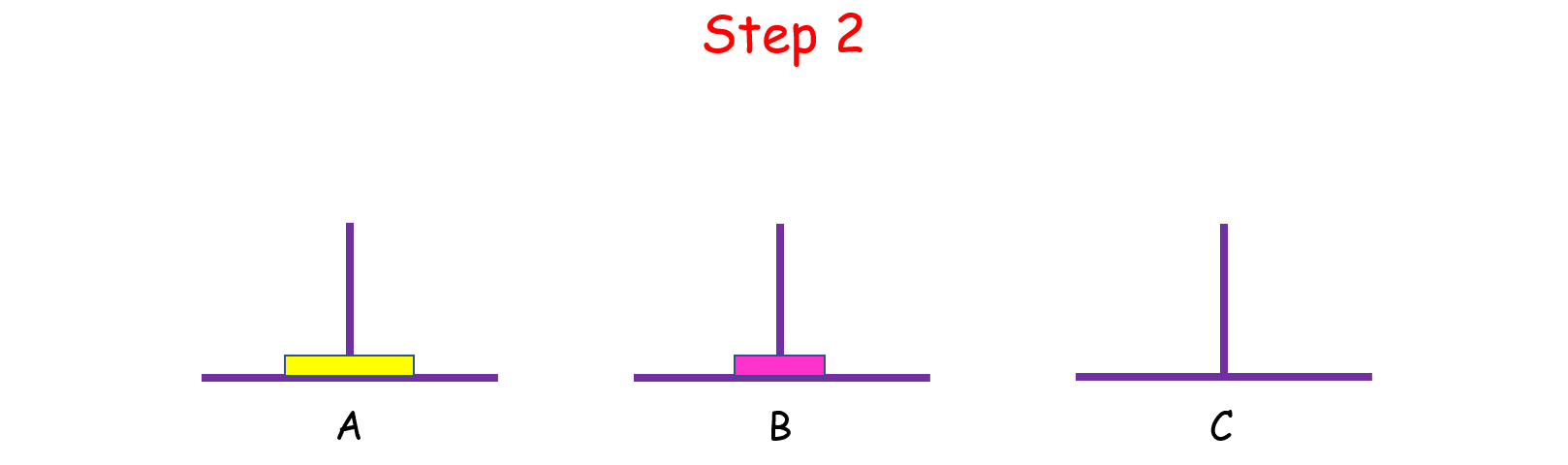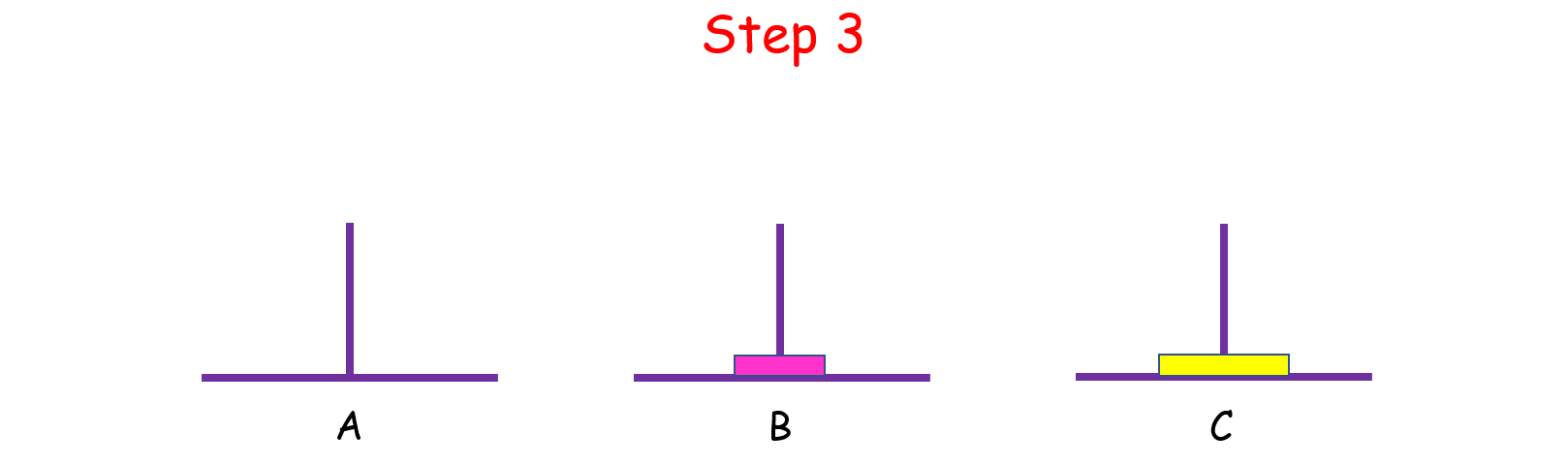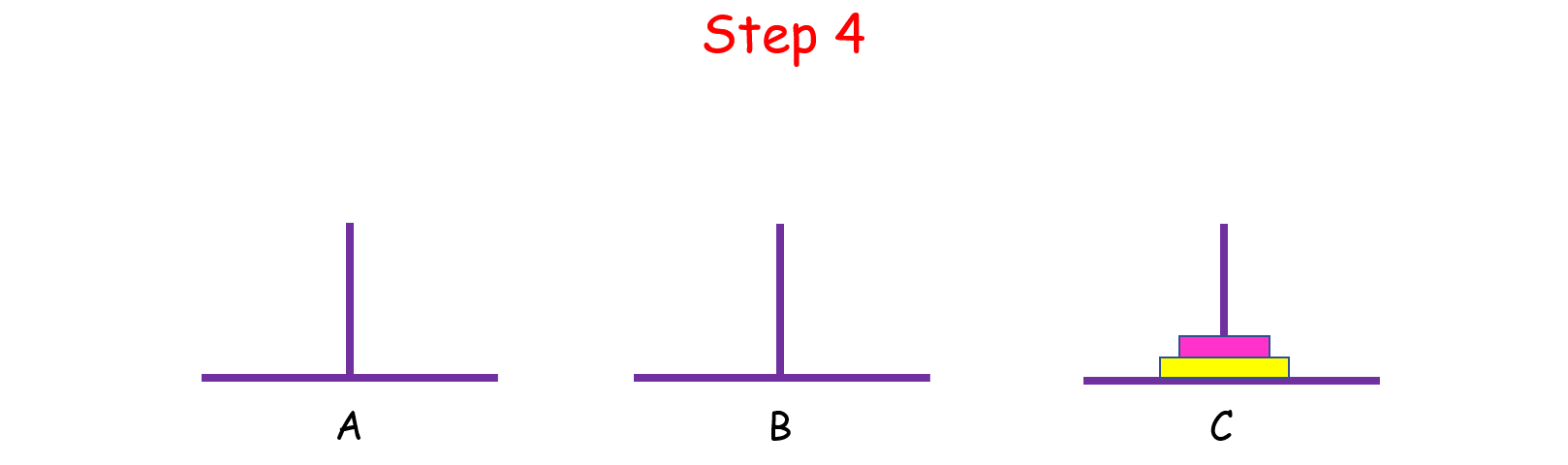
如果 n > 2 呢?思路和上面是一样的,我们把 n 个盘子也看成两个部分,一部分有 1 个盘子,另一部分有 n - 1 个盘子。
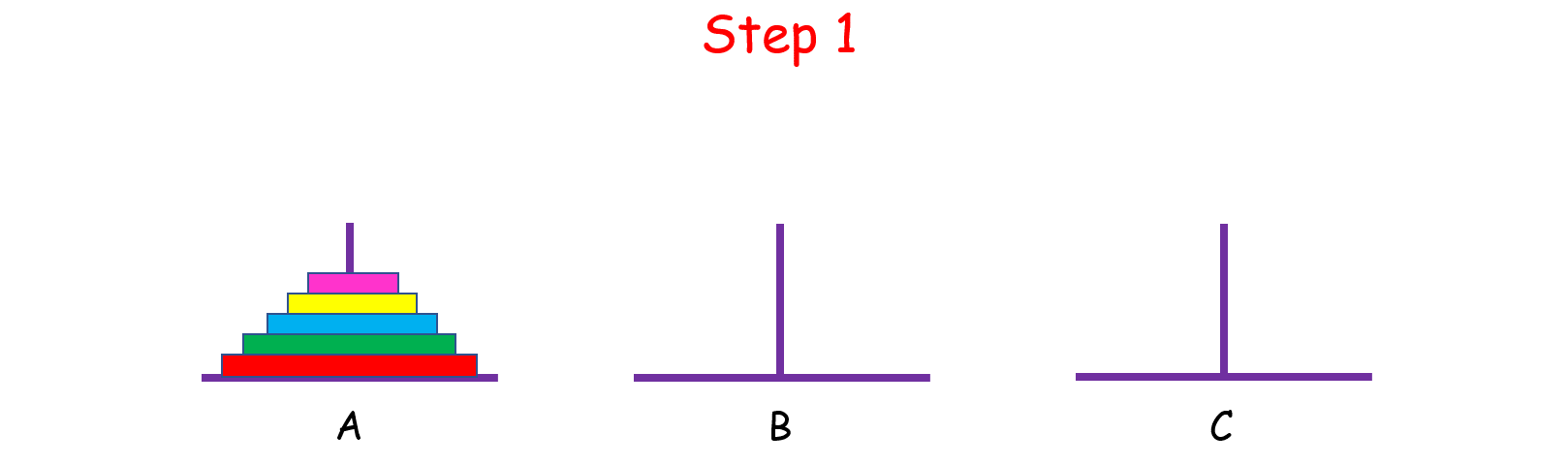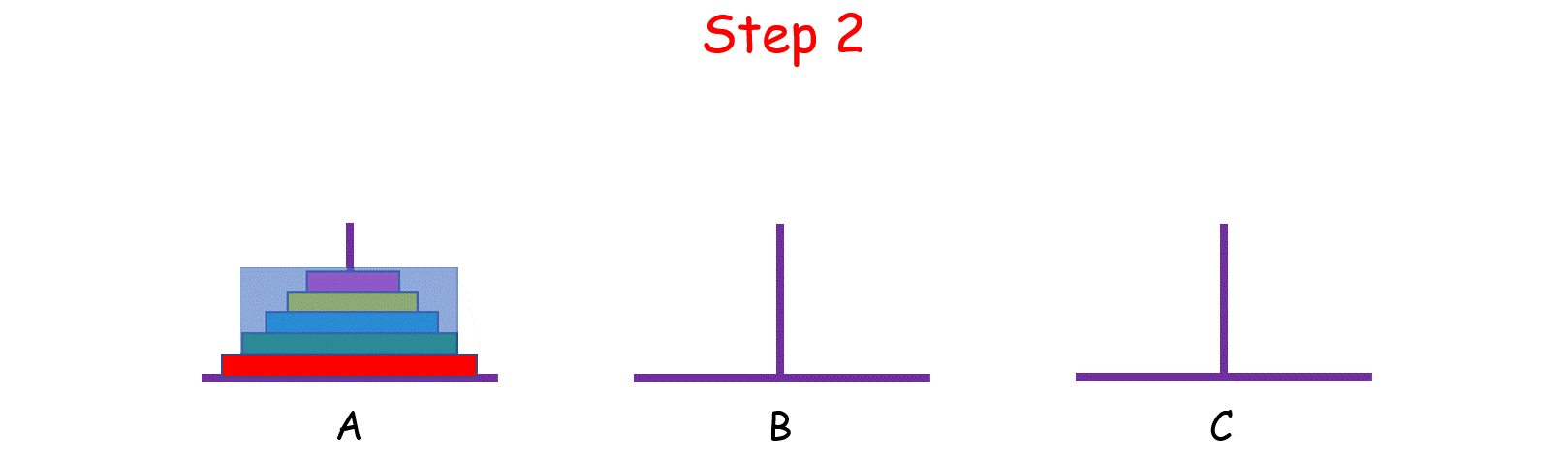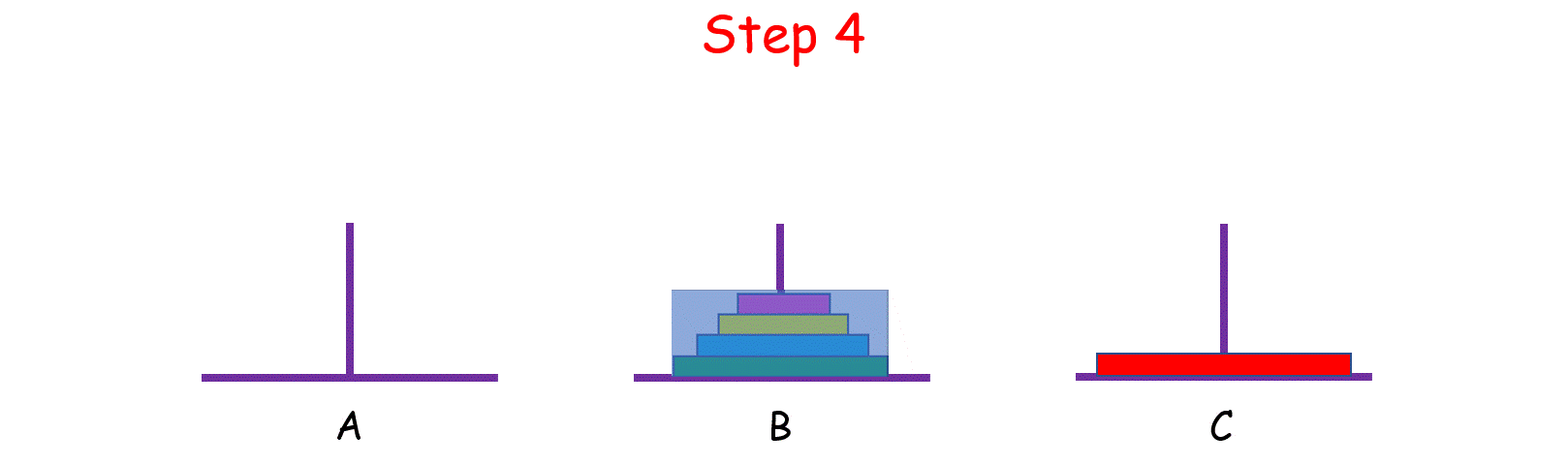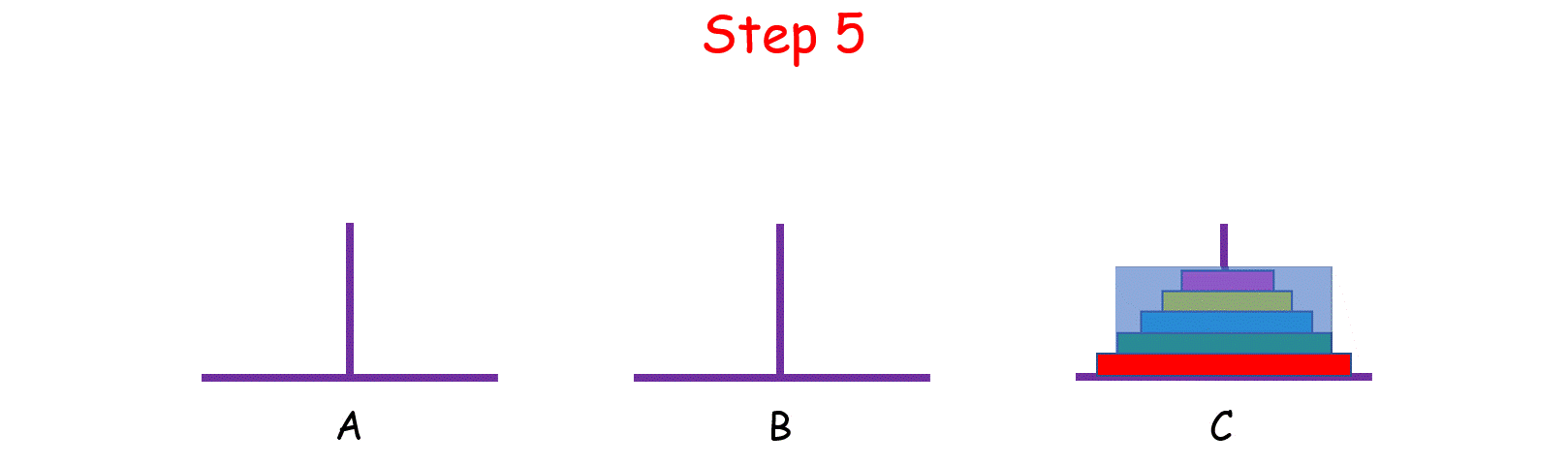
观察上图,你可能会问:“那 n - 1 个盘子是怎么从 A 移到 C 的呢?”
当你在思考这个问题的时候,就将最初的 n 个盘子从 A 移到 C 的问题,转化成了将 n - 1 个盘子从 A 移到 C 的问题, 依次类推,直至转化成 1 个盘子的问题时,问题也就解决了。这就是分治的思想。
而实现分治思想的常用方法就是递归。不难发现,如果原问题可以分解成若干个与原问题结构相同但规模较小的子问题时,往往可以用递归的方法解决。具体解决办法如下:
-
n = 1 时,直接把盘子从 A 移到 C;
-
n > 1 时,
-
先把上面 n - 1 个盘子从 A 移到 B(子问题,递归);
-
再将最大的盘子从 A 移到 C;
-
再将 B 上 n - 1 个盘子从 B 移到 C(子问题,递归)。
-
Java代码
class Solution {
public void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {
/*
1.先将A柱子中的n-1个的圆盘移动到B柱子
2.再将A柱子中最后1个圆盘移动到C柱子
3.最后将B柱子的n-1个圆盘移动到C柱子
*/
int n = A.size();
move(n, A, B, C);
}
/*
其中A为原始柱子;B为辅助柱子;C为目标柱子(与位置有关,那么list都有可能)
*/
private void move(int n, List<Integer> A, List<Integer> B, List<Integer> C) {
// A中只剩下1个圆盘了,直接移动到C柱子后结束
if (n == 1) {
C.add(A.remove(A.size() - 1));// 将A柱子中最后1个圆盘移动到C柱子
return;
}
// 1.先将的A柱子中的n-1个的圆盘移动到B柱子(此时B为目标柱子,A为原始柱子)
move(n - 1, A, C, B);
// 2.再将的A柱子中最后1个圆盘移动到C柱子
C.add(A.remove(A.size() - 1));
// 3.最后将B柱子的n-1个圆盘移动到C柱子(此时C为目标柱子,B为原始柱子)
move(n - 1, B, A, C);
}
}
C++代码
class Solution {
public:
void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {
int n = A.size();
move(n, A, B, C);
}
void move(int n, vector<int>& A, vector<int>& B, vector<int>& C){
if (n == 1){
C.push_back(A.back());
A.pop_back();
return;
}
move(n-1, A, C, B); // 将A上面n-1个通过C移到B
C.push_back(A.back()); // 将A最后一个移到C
A.pop_back(); // 这时,A空了
move(n-1, B, A, C); // 将B上面n-1个通过空的A移到C
}
};
复杂度分析
- 时间复杂度:O(2^n-1)。一共需要移动的次数。
- 空间复杂度:O(1)。