二叉排序树
二叉排序树又称为二叉查找树。它或者是一颗空树,或者是具有下列性质的二叉树:
若它的左子树不为空,则左子树上所有节点的值均小于它的根结构的值;若它的右子树不为空,则右子树上所有节点的值均大于它的根结构的值;它的左、右子树也分别为二叉排序树。
构造一颗二叉排序树的目的,往往不是为了排序,而是为了提高查找和插入删除关键字的速度。
二叉排序树的操作:
查找:对比节点的值和关键字,相等则表明找到了;小了则往节点的左子树去找,大了则往右子树去找,这么递归下去,最后返回布尔值或找到的节点。插入:从根节点开始逐个与关键字进行对比,小了去左边,大了去右边,碰到子树为空的情况就将新的节点链接。删除:如果要删除的节点是叶子,直接删;如果只有左子树或只有右子树,则删除节点后,将子树链接到父节点即可;如果同时有左右子树,则可以将二叉排序树进行中序遍历,取将要被删除的节点的前驱或者后继节点替代这个被删除的节点的位置。
"""
定义一个二叉树节点类。
以讨论算法为主,忽略了一些诸如对数据类型进行判断的问题。
"""
def__init__(self,data,left=None,right=None):
"""
初始化
:paramdata:节点储存的数据
:paramleft:节点左子树
:paramright:节点右子树
"""
self.data=data
self.left=left
self.right=rightclassBinarySortTree:
"""
基于BSTNode类的二叉排序树。维护一个根节点的指针。
"""
def__init__(self):
self._root=None
defis_empty(self):
returnself._rootisNone
defsearch(self,key):
"""
关键码检索
:paramkey:关键码
:return:查询节点或None
"""
bt=self._rootwhilebt:
entry=bt.dataifkey<entry:
bt=bt.leftelifkey>entry:
bt=bt.rightelse:returnentryreturnNone
definsert(self,key):
"""
插入操作
:paramkey:关键码
:return:布尔值
"""
bt=self._rootifnotbt:
self._root=BSTNode(key)return
whileTrue:
entry=bt.dataifkey<entry:ifbt.leftisNone:
bt.left=BSTNode(key)return
bt=bt.leftelifkey>entry:ifbt.rightisNone:
bt.right=BSTNode(key)return
bt=bt.rightelse:
bt.data=keyreturn
defdelete(self,key):
"""
二叉排序树最复杂的方法
:paramkey:关键码
:return:布尔值
"""
p,q=None,self._root#维持p为q的父节点,用于后面的链接操作
ifnotq:
print("空树!")return
whileqandq.data!=key:
p=qifkey<q.data:
q=q.leftelse:
q=q.rightifnotq:#当树中没有关键码key时,结束退出。
return
#上面已将找到了要删除的节点,用q引用。而p则是q的父节点或者None(q为根节点时)。
ifnotq.left:ifpisNone:
self._root=q.rightelifqisp.left:
p.left=q.rightelse:
p.right=q.rightreturn
#查找节点q的左子树的最右节点,将q的右子树链接为该节点的右子树
#该方法可能会增大树的深度,效率并不算高。可以设计其它的方法。
r=q.leftwhiler.right:
r=r.right
r.right=q.rightifpisNone:
self._root=q.leftelifp.leftisq:
p.left=q.leftelse:
p.right=q.leftdef__iter__(self):
"""
实现二叉树的中序遍历算法,
展示我们创建的二叉排序树.
直接使用python内置的列表作为一个栈。
:return:data
"""
stack=[]
node=self._rootwhilenodeorstack:whilenode:
stack.append(node)
node=node.left
node=stack.pop()yieldnode.data
node=node.rightif__name__=='__main__':
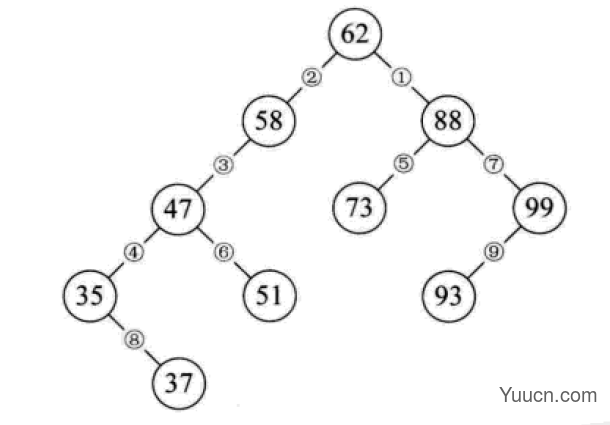
lis=[62,58,88,48,73,99,35,51,93,29,37,49,56,36,50]
bs_tree=BinarySortTree()foriinrange(len(lis)):
bs_tree.insert(lis[i])#bs_tree.insert(100)
bs_tree.delete(58)foriinbs_tree:
print(i,end="")#print("\n",bs_tree.search(4))
相关推荐:《Python视频教程》
二叉排序树总结:
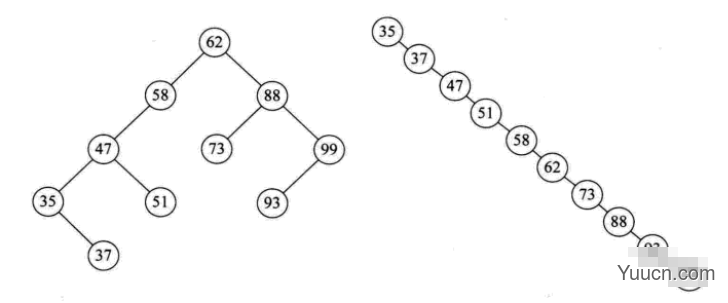
二叉排序树以链式进行存储,保持了链接结构在插入和删除操作上的优点。在极端情况下,查询次数为1,但操作次数不会超过树的深度。也就是说,二叉排序树的查找性能取决于二叉排序树的形状,也就引申出了后面的平衡二叉树。给定一个元素集合,可以构造不同的二叉排序树,当它同时是一个完全二叉树的时候,查找的时间复杂度为O(log(n)),近似于二分查找。当出现最极端的斜树时,其时间复杂度为O(n),等同于顺序查找,效果最差。
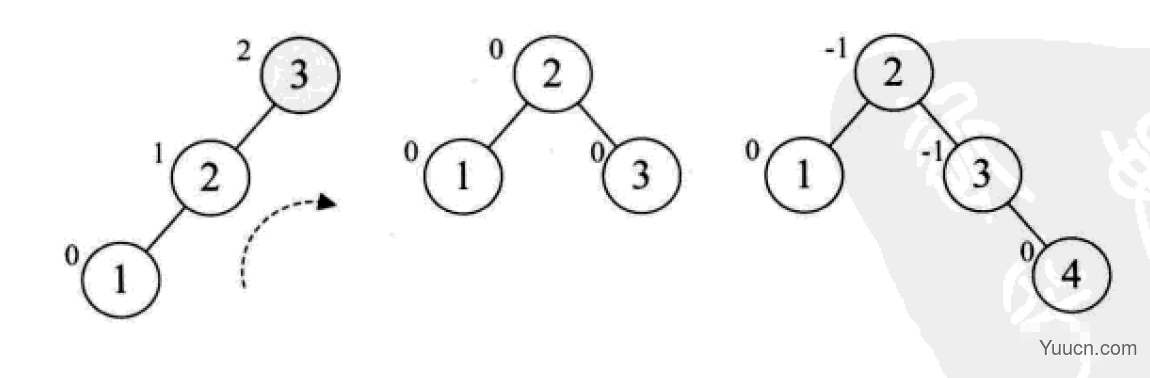
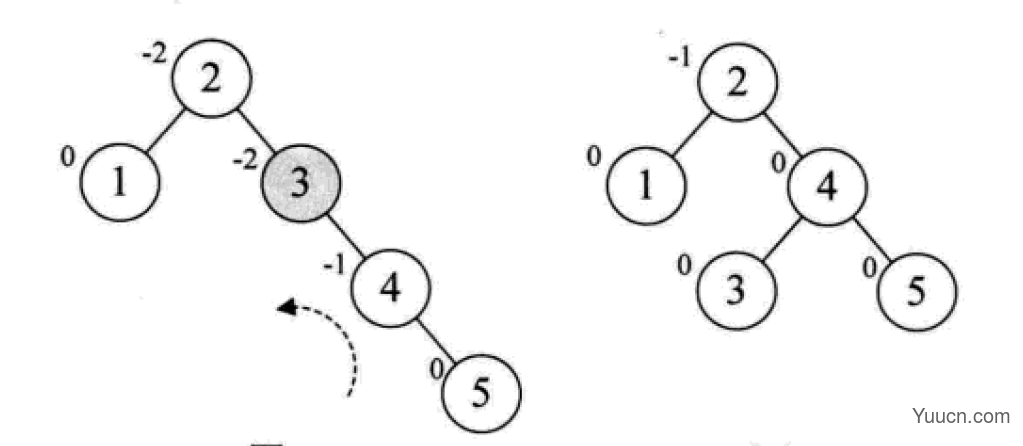
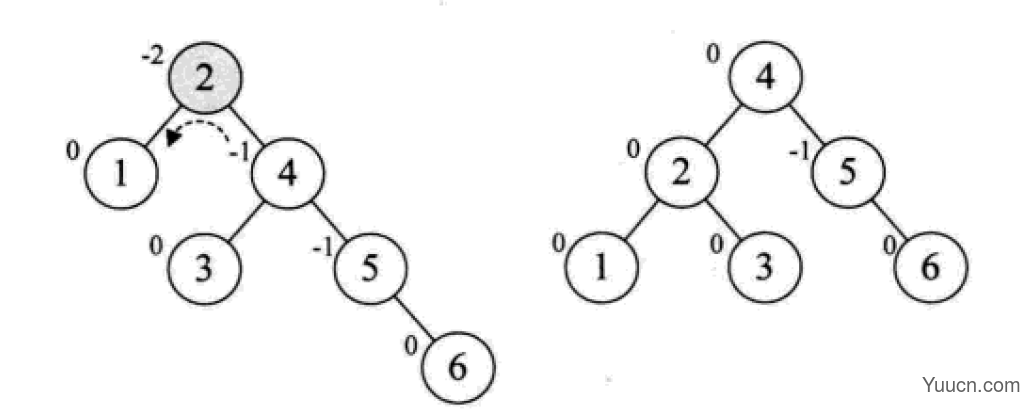
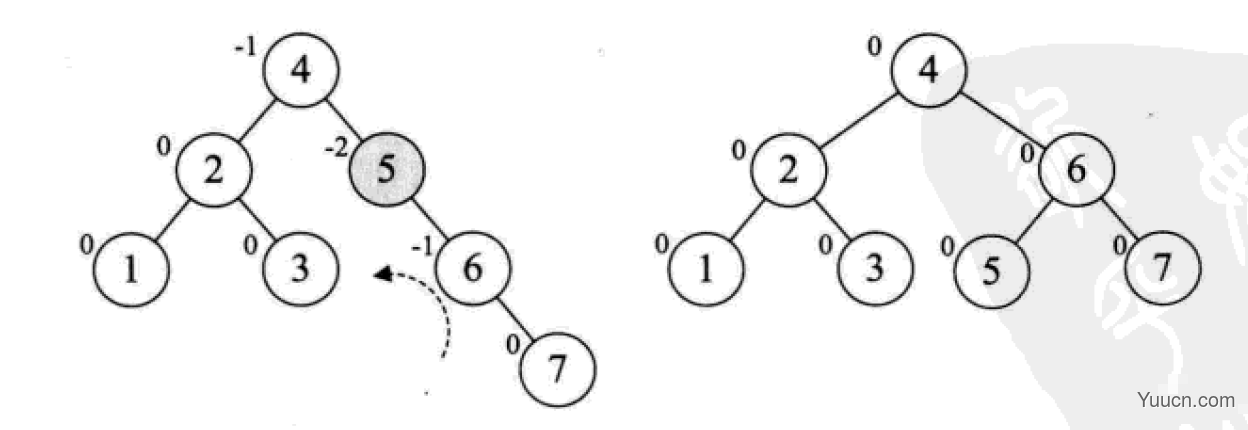
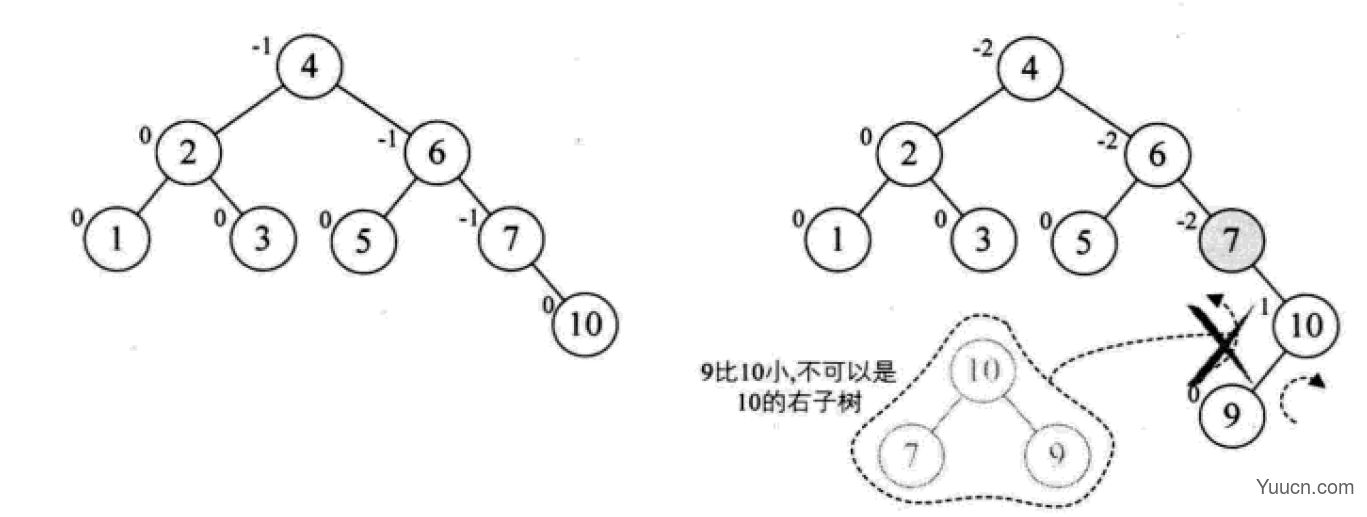
平衡二叉树
平衡二叉树(AVL树,发明者的姓名缩写):一种高度平衡的排序二叉树,其每一个节点的左子树和右子树的高度差最多等于1。
平衡二叉树首先必须是一棵二叉排序树!
平衡因子(Balance Factor):将二叉树上节点的左子树深度减去右子树深度的值。
对于平衡二叉树所有包括分支节点和叶节点的平衡因子只可能是-1,0和1,只要有一个节点的因子不在这三个值之内,该二叉树就是不平衡的。
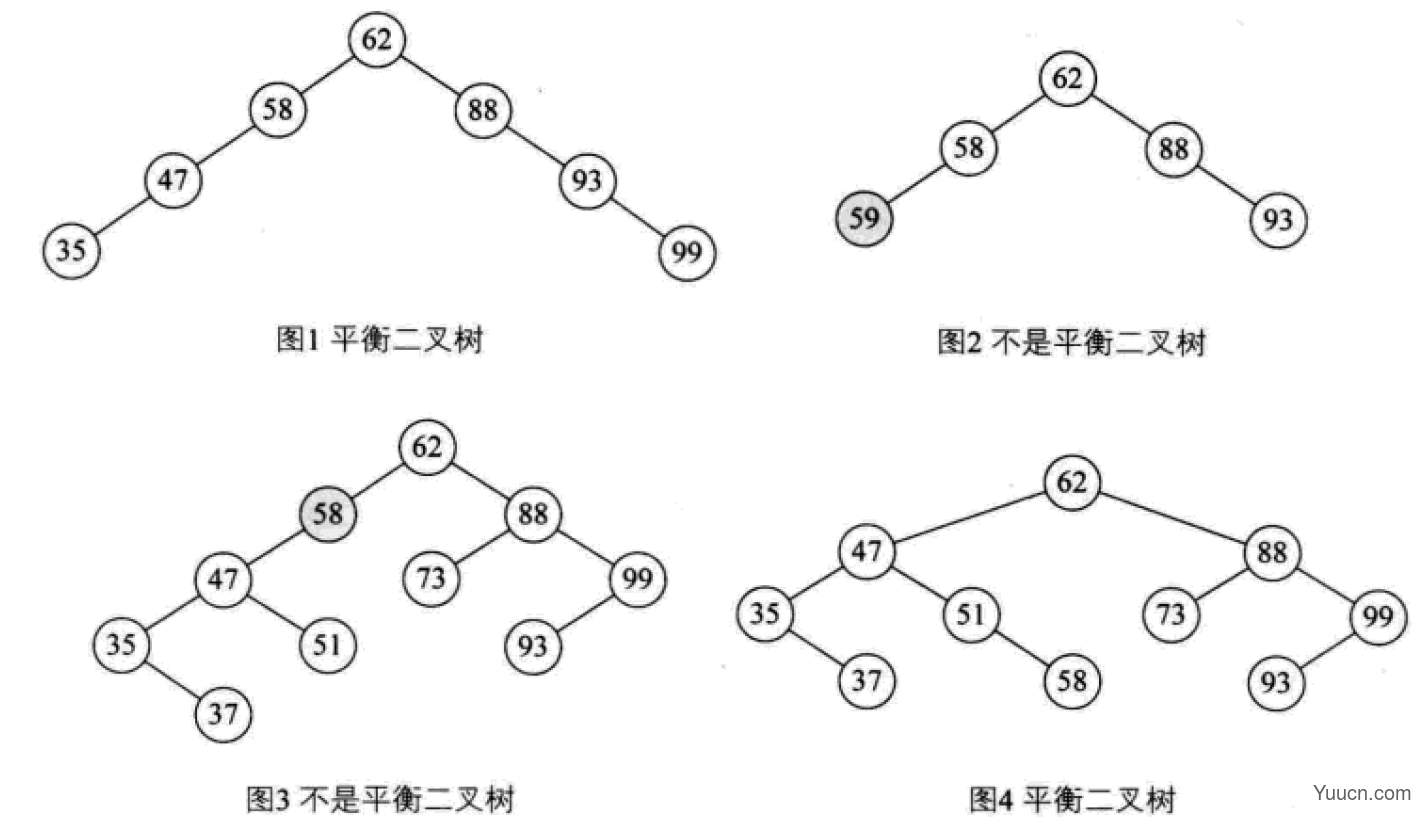
最小不平衡子树:距离插入结点最近的,且平衡因子的绝对值大于1的节点为根的子树。
平衡二叉树的构建思想:每当插入一个新结点时,先检查是否破坏了树的平衡性,若有,找出最小不平衡子树。在保持二叉排序树特性的前提下,调整最小不平衡子树中各结点之间的连接关系,进行相应的旋转,成为新的平衡子树。
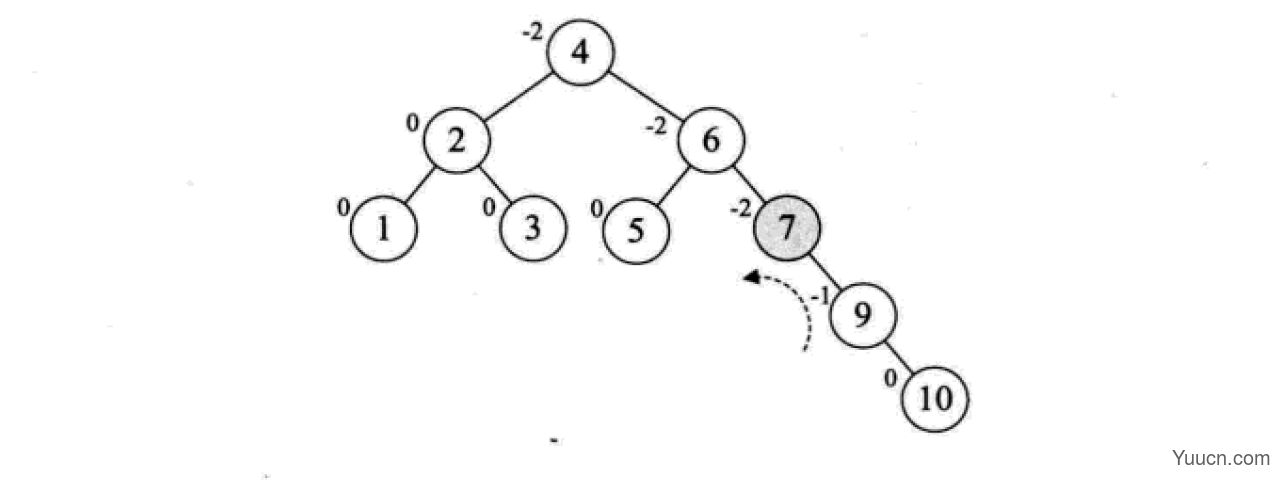
下面是由[1,2,3,4,5,6,7,10,9]构建平衡二叉树