目录
一、因果推断介绍
1.1 什么是因果推断
1.2为什么研究因果推断
1.3因果推断阶梯
1.4因果推断问题分类
二、因果推断理论框架
2.1 定义(这些定义后面会经常用到)
2.2 Assumptions(三大基本假设)
三、因果效应估计
3.1 因果效应问题定义
3.2 消除偏差方法
3.2.1 倾向性得分匹配
3.2.2 双重机器学习
3.2.3 双重稳健学习
3.3估计因果效应
四、待补充
一、因果推断介绍
1.1 什么是因果推断
因果推断是基于统计学方法刻画变量之间的因果关系。
参考:
- 关于因果推断你知道多少:关于因果推断你知道多少
1.2为什么研究因果推断
机器学习预测未来,因果推断改变未来。
1.3因果推断阶梯
-
第一层级(
关联
):从数据中观察到哪些相关规律?是对历史数据的总结。 -
第二层级(
干预
):如果采取某个行动,会产生什么结果?是面向未来的推测。 -
第三层级(
反事实
):如果当时采取了另外一个行动,结果会是怎样?是面向过去的反思。
1.4因果推断问题分类
因果推断解决的问题可以分成两类:
-
因果关系发现
(Causal Discovery):从数据中发掘哪些变量之间存在因果关系,谁是因、谁是果。 -
因果效应评估
(Causal Effect Estimatation):评估一个变量变化后能多大程度影响另外一个变量。
二、因果推断理论框架
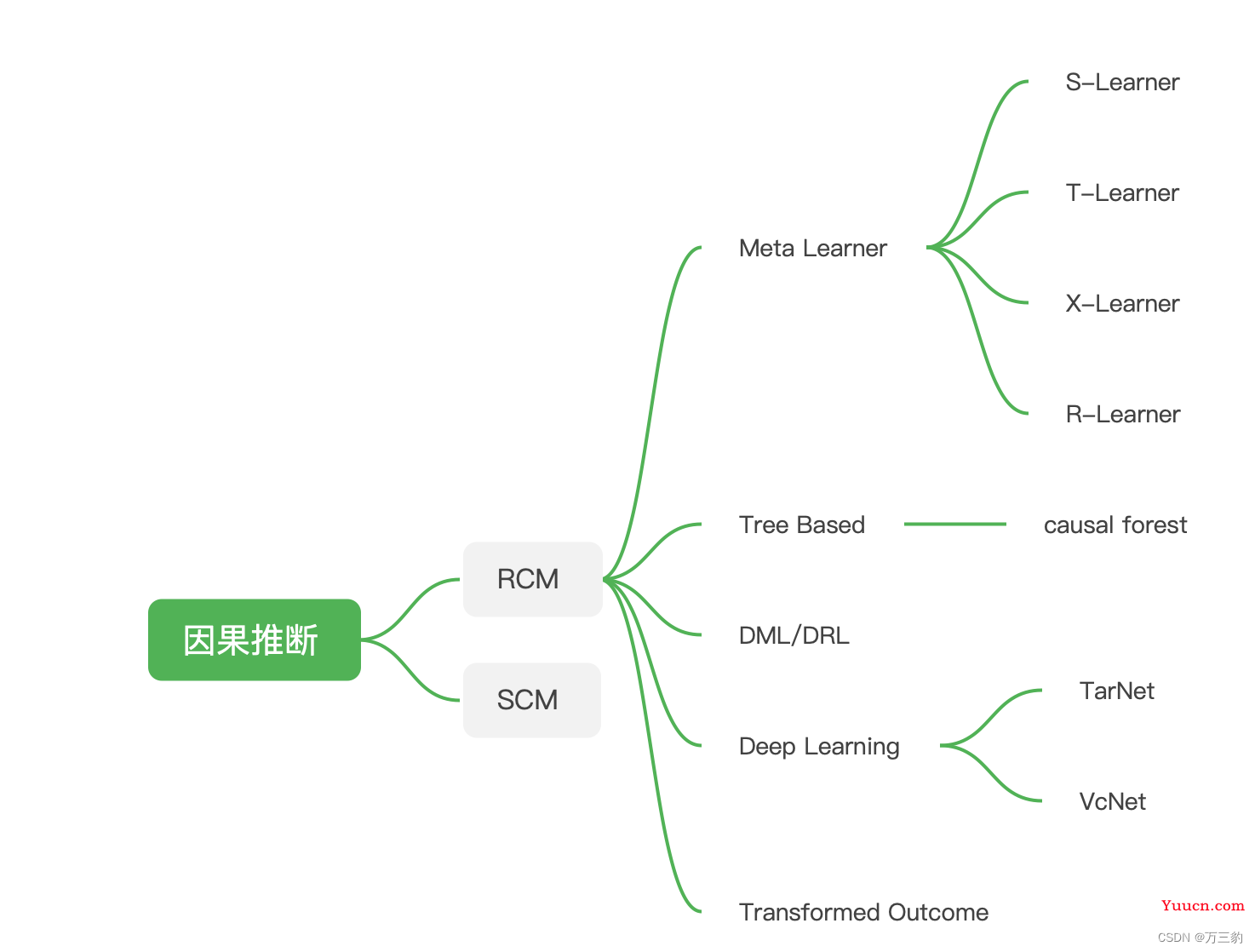
为形式化地定义和研究因果推断,多种理论框架被建立,其中最著名的是潜在结果框架(Potential Outcome Framework)和结构因果模型(Structural Causal Model,简称SCM),前者由Donald Rubin提出,所以也被称为Rubin Causal Model(简称RCM)。
2.1 定义(这些定义后面会经常用到)
-
unit:因果推断里最小的物理单元,比如一个人
-
treatment:施加给unit的动作,比如吃药。一般用W表示,比如W=1表示吃药,W=0表示不吃药
-
outcome:某个unit在某个treatment下的表现,比如吃药之后好了还是没好。一般用Y表示,Y(W=1)表示这个人在吃药后的表现,如果Y=1表示病好了,则Y(W=1)=1的含义是这个人吃药之后病好了。同理,Y(W=1)=0表示这个人吃药之后病没有好
-
observed outcome:unit在实际的treatment下的表现,这个人实际上是吃了这个药的
-
potential outcome:unit在潜在的treatment下的表现,比如这个人没有吃药,但是如果吃药了,其表现就是potential outcome
-
treatment effect:施加了treatment后的增量效果(or 增益),比如吃药之后相比于没有吃药,其治愈率提升了多少,其存在如下3个维度:
-
Average Treatment Effect (
ATE) ,整个群体的因果效应 :ATE = E[Y(W=1)] - E[T(W=0)],所有人的平均treatment effect -
Conditional Average Treatment Effect (
CATE),
条件平均因果效应:CATE = E[Y(W = 1)|X = x] − E[Y(W = 0)|X = x],在特征X=x的子人群里面treatment effect,X为筛选个体的特征值,也被称为
协变量。 -
Individual Treatment Effect (
ITE),
个体因果效应:ITEi = Yi (W = 1) − Yi (W = 0),某个unit(人维度)的treatment effect
-
-
数据格式:是这样的三元组,<X,W,Y>,X是特征,W是施加的treatment,Y是outcome
参考:
- 2020年因果推断综述《A Survey on Causal Inference》 - 知乎
2.2 Assumptions(三大基本假设)
1、Stable Unit Treatment Value Assumption (SUTVA):The potential outcomes for any unit do not vary with the treatment assigned to other units, and, for each unit, there are no different forms or versions of each treatment level, which lead to different potential outcomes.
-
每个人对各个treatment的outcome是固定,不会被其他人影响,人和人之间是独立的
-
一个treatment只有一个版本,比如某个药物,在不同的剂量下,则对应不同的treatment
2、Ignorability: Given the background variable, X , treatment assignment W is independent to the potential outcomes, i.e:
-
如果两个人的特征X相同,则他们的potential outcome(即Y(W=0)、Y(W=1))是相同的,不论在哪种的treatment下,即outcome和treatment独立
-
具有相同特征X的人群,每个人接受到哪种treatment是完全随机的,概率都相同
-
不存在某个在X之外的隐变量,同时影响outcome和treatment,使得treatment和outcome相关,因此这个假设又称unconfoundedness assumption
3、Positivity:For any value of X , treatment assignment is not deterministic: P(W = w |X = x) > 0, ∀ w and x .
-
即对于某个特征X下的人群,每个人都有概率被施加任何treatment,并且人群中存在所有的treatment
上述假设只是让我们预估treatment effect能更准确一些,但是由于存在反事实的问题,导致没有ground truth,因此预估值不一定准确。如何预估潜在的treatment effect始终是因果推断的核心问题。
三、因果效应估计
3.1 因果效应问题定义
因果推断里将采取动作称为
施加干预(
Treatment),而因果效应为施加干预与否对结果造成的差异。注意,如果想准确衡量差异,需保证其他因素不变而只有“施加干预与否”这个变化。最好的情形应该是:存在两个平行时空,分别施加和未施加干预得到两个结果,
两个结果的差异就是干预产生的因果效应。
施加干预(
Treatment),而因果效应为施加干预与否对结果造成的差异。注意,如果想准确衡量差异,需保证其他因素不变而只有“施加干预与否”这个变化。最好的情形应该是:存在两个平行时空,分别施加和未施加干预得到两个结果,
两个结果的差异就是干预产生的因果效应。
事实上不存在平行时空,我们不能同时对一个群体既施加干预又不施加干预,而只能观察到其中的一种情况,对于未观察的情况我们称之为
反事实的(Counterfactual)。理论上,可以通过随机控制实验(Random Control Trial,RCT)来解决这个问题:将群体随机分成两组,一组施加干预(
实验组),另一组不施加干预(
控制组/
对照组)。这种方法称为
实验性研究,广泛应用的AB实验方法其实就是同样的思路。
反事实的(Counterfactual)。理论上,可以通过随机控制实验(Random Control Trial,RCT)来解决这个问题:将群体随机分成两组,一组施加干预(
实验组),另一组不施加干预(
控制组/
对照组)。这种方法称为
实验性研究,广泛应用的AB实验方法其实就是同样的思路。
不过,实验组和控制组之间往往很难实现完全随机,导致两组之间会存在天然差异,即
偏差(Bias)。另外,很多时候无法进行随机控制实验,这时只能基于现有观察到的数据,采取一定方法从中筛选出“实验组”和“控制组”,这称为
观察性研究或者
准实验方法,此时的“实验组”和“控制组”更容易出现偏差。
偏差(Bias)。另外,很多时候无法进行随机控制实验,这时只能基于现有观察到的数据,采取一定方法从中筛选出“实验组”和“控制组”,这称为
观察性研究或者
准实验方法,此时的“实验组”和“控制组”更容易出现偏差。
导致偏差的原因包括:
(1)混杂偏差:同时对Treatment和结果有影响的因素叫
混杂因子(Confounder),它的存在会导致偏差。消除混杂偏差的方法是将混杂因子控制住,再去度量Treatment和结果的关系。
混杂因子(Confounder),它的存在会导致偏差。消除混杂偏差的方法是将混杂因子控制住,再去度量Treatment和结果的关系。
比如在研究“就诊频率与寿命的影响”时,身体状况会同时影响就诊频率和寿命,它就是个混杂因子,如果不消除其影响,就会产生“去医院不利于身体健康”的谬论。
如果针对相同身体状况的人群(即控制住“身体状况”这个因子)对比不同就诊频率下寿命的差异,就能去除偏差。
(2)
选择偏差:不管是实验性研究还是观察性研究,评估通常都是在一个筛选出来的样本子集上进行,如果样本子集不能代表总体,则会导致选择偏差(或称样本偏差)。
选择偏差:不管是实验性研究还是观察性研究,评估通常都是在一个筛选出来的样本子集上进行,如果样本子集不能代表总体,则会导致选择偏差(或称样本偏差)。
比如在研究“就诊频率与寿命的影响”时,为了控制身体状况这个混杂因子,我们筛选特定年龄50岁、身高175CM、体重70KG、血压120/80mmHg、心率80次/分的人群对比不同就诊频率下的寿命,此时得到的结论适用于人群总体时会有选择偏差。
因此,偏差是让从数据中的得到相关性不能推导出因果性的主要原因。
3.2 消除偏差方法
当Treatment T和Outcome Y受共同的因素X影响时,就会发生混淆偏差。为去除偏差,需要控制住X,使得实验组和控制组的特征X分布一致,此时的Treatment独立于Y,满足无混淆假设,之后就可以正确地估计因果效应。去除混淆偏差的方法包括:
3.2.1 倾向性得分匹配
Propensity Score Matching,PSM。
方法:首先通过X预测T,得到一个条件概率P(T|X),也称之为倾向性得分(Propensity Score, PS),之后基于PS得分进行匹配,对于实验组的每一个样本,在对照组找到与之匹配(即二者相似)的一个样本,组成一个样本对,最后基于所有的样本对进行因果建模。
原理:理解了倾向性得分后,PSM也就是基于PS得分进行匹配,即对于实验组的每一个样本,在对照组找到与之匹配(即二者相似)的一个样本,组成一个样本对,最后基于所有的样本对进行因果建模,以达到控制混淆的目的。根据匹配方式的不同,PSM有两种方法:距离和权重。
优点:原理简单,容易理解。倾向性得分可以使用任意ML模型。
缺点:
需要对PS得分过小或者PS得分过大的样本进行处理。
需要对PS得分过小或者PS得分过大的样本进行处理。
应用场景:适用于二值或者离散Treatment场景
疑问:
X预测T,在实验组训练还是在实验组和对照组一起训练?
X预测T,在实验组训练还是在实验组和对照组一起训练?
3.2.2 双重机器学习
Double Machine Learning, DML。
方法:首先通过X预测T,与真实的T作差,得到一个T的残差,然后通过X预测Y,与真实的Y作差,得到一个Y的残差,预测模型可以是任何ML模型,最后基于T的残差和Y的残差进行因果建模。
原理:DML采用了一种残差回归的思想。
优点:原理简单,容易理解。预测阶段可以使用任意ML模型。
缺点:
需要因果效应为线性的假设。
需要因果效应为线性的假设。
应用场景:适用于连续Treatment且因果效应为线性场景
3.2.3 双重稳健学习
Doubly Robust Learning, DRL。
方法:首先通过X预测T,得到一个倾向性得分P(X),然后通过(X,T)预测Y,预测模型可以是任何ML模型,最后基于X和预测的Y进行因果建模。
原理:DML采用了一种残差回归的思想。
优点:只需倾向性得分预测模型和目标值预测模型的其中一个预测准确即可,预测阶段可以使用任意ML模型。
缺点:
当两个模型都表现不佳时,误差会变大。
当两个模型都表现不佳时,误差会变大。
应用场景:适用于离散Treatment场景。
3.3估计因果效应
四、待补充
- 因果效应估计方法介绍
- 因果效应评估方式
- 因果效应估计方法代码实现
- 因果森林分裂方式
- 具体应用/运筹优化
- 相关论文学习