模糊控制
文章目录
- 模糊控制
- 前言
- 一、模糊控制是什么?与神经网络的区别?
- 二、模糊控制原理
-
- 1.模糊化
- 2.模糊规则
- 3.模糊推理
- 4.解模糊化
- 三、模糊控制算法实例解析(含代码)
-
- 1、选择观测量和控制量
- 参考
前言
鉴于个人学习方向并不在此,所以此文章仅作为个人学习笔记使用,主要介绍理论以及学习过程,仅供参考!
一、模糊控制是什么?与神经网络的区别?
为什么要有模糊控制、为什么要用神经网络、为什么还要将两者结合,还有那么多不同的结合方法等等问题的关键。两个理解模糊神经网络的重要前提:
(1)模糊控制的基本思想是利用计算机来实现人的控制经验[;
(2)人工神经网络是一种应用类似于大脑神经突触联接的结构进行信息处理的数学模型;
在历史的发展中,人类始终以自己为中心来建立世界的模型。数学的哲学本质也可以理解为人们对客观世界建立的主观模型,数学和哲学这两个东西是真的好,因为这是从另一种角度去阅读自然。模糊控制的诞生始于对客观世界复杂性和不确定性,当人们尝试探索一些物理过程内部的精确机理时,会发现有很多问题,“当一个系统复杂性增大时,人们能使它精确化的能力会降低,当达到一定阈值时,复杂性与精确性相互排斥”。这就意味着人无法完全掌握一些十分复杂的系统,实际上在实际应用中,也并不需要掌握,因为那些生产线上的工人不知道系统内部机理,他们控制系统的效果依然很好。这就是模糊控制,利用人的经验而不是系统内部原理来实现复杂系统控制。“人”或者“人脑”才是这个自然最完美的控制器,因此模拟人脑的过程就是人们为了实现完美控制的重要途经。
二、模糊控制原理
模糊控制是一种最简单的人脑模拟器
1.模糊化
import numpy as np
import pandas as pd
人在处理外部信息的时候,并没有量化数据这个概念,而是根据自己的经验来判断。比如,你现在的位置与帝都的距离。你可能觉得很远,因为你在魔都。但是如果你自己在河北、天津,你就觉得不是很远。而你在5环,你依旧觉得你依然离帝都很远。这个“很远”,“不是很远”其实就是模糊化,因为人的“传感器”不能给你一个完全精确的距离,但你也不必关心,你关心的是这个距离你打车大概花多少钱,比如便宜、还行、贵,也是模糊化的概念。这里其实输入就是距离这个模糊概念,输出就是花的钱这个模糊化后的概念。这些概念人是可以理解的,但是电脑可不行,要想实现自动化的控制,就需要把这些概念通过一些转换,映射到电脑里面去做计算。隶属度函数、模糊集合、模糊运算…其实这些总结为一句话就是如果把这些东西放到电脑里该怎么计算的。
官方定义:
(1)论域:由被考虑对象的所有元素的全体组成的基本集合,对应“全集”这个概念;
(2)模糊子集:设论域 E ,E 到闭区间 [0,1] 的任一映射 ,它确定了 E 的一个模糊子集,简称模糊集。
有了模糊子集的定义后就可以进入正题了 —— 隶属度函数。隶属度函数是模糊控制中的最重要的概念之一,它是由清晰输入到模糊输入的转变,是精确值到模糊语言的转化,也是模糊控制的第一步。但是隶属度函数的设计上有很多要求,比如要符合客观规律,不能是主观臆想,还要能反映出客观模糊现象的具体特征。实际上,模糊隶属度函数的确定取决于设计控制系统的人,灵活性很大。灵活性大是好事,但也是坏事。隶属度函数的确定已经可以初窥人们对控制器的追求。灵活性通常意味着人们可以自己随便设定隶属度函数,而实际的应用中,很明显不是所有人都能设计初适应性特别好、精度特别高的隶属度函数。所以大家就都用那些设计好的隶属度函数,可以理解为专家设计的。
模糊隶属度函数的确定方法:
(1)模糊统计法
(2)二元对比排序法
(3)专家经验法
前面说灵活性,其实为了控制系统的性能着想,就要优化设计过程中的每一步,专家经验给定的就是比较准确的隶属度函数。总之不知道的时候就听专家的吧。其实,采用专家经验也是很多文献中采用的优化办法。
(4)演绎推理法
(5)角模糊集法
(6)神经网络法
神经网络也可以理解为是一种专家经验,通过试验数据或理论数据对一个网络进行训练,节省了训练“专家”的时间,并且降低了主观臆测的风险,因为神经网络是完全凭借数据说话的。你会发现在很多场合中,尤其是奥运会的评分项目中,人们都倾向于将评分尽量打的客观,避免“黑哨”,所以才有这个领域的专家,那么一旦神经网络模型完美模拟了人,那这些专家可真要喝西北风了。
(7)遗传算法
(8)归纳推理
(9)借助常见模糊分布函数 (最常用)
这里就不用说了,三角型、高斯型隶属度函数。
模糊化得到的结果通常可以表示成语言变量,但是在计算机中则表现为一个具体的数值—隶属度。接下来就需要对这些隶属度做进一步处理——设计规则。
2.模糊规则
模糊规则的设计实际上也十分灵活,取决于你的被控系统特性。比如要控制一个点的温度为50℃恒温。当它为40℃的时候你觉得可能是“偏低”,而我觉得“很低”,专家觉得“这样就行”,在误差范围内。那么结果就是你的行动是“稍微加热一下”,我的行动就是“全力加热”,专家直接“睡大觉”去了。这些行动其实就是规则,规则通常表现为查找表的形式,就是你让计算机去按照你设定的规则表去行动,如下表所示:
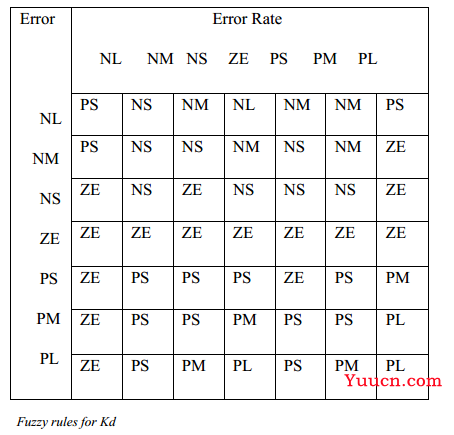
模糊控制最常采用的输入是实际输出与期望输出的误差(error)和误差变化率(error rate)两个量。这里需要做以下说明:
假设模糊控制全部采用误差与误差变化率的7 * 7规则表作为控制规则,那么当系统为单输入单输出(SISO)情况下,有7 * 7 * 1 * 1个规则,其中这个1为单输入,第二个1为单输出。当系统为1输入2输出的情况下,可以推理,每个输出应对应一个规则表,则两个输出有7 * 7 * 1 * 2个规则。这里输入为1的原因是评价系统的参数为单一参数,即如果你控制一个系统的温度,那么就根据这个温度的误差和误差变化率来设计对应的输出条件。则对于多输入的情况下 7 * 7 * N * M个规则,我上一篇写了模糊控制静态特性中提到了模糊规则的设计,这对人工设计来说,工作量实在太大。这里我们就只说SISO系统的模糊控制。
3.模糊推理
模糊推理是模糊规则运算的过程。对于一个模糊系统或者一个模糊过程,人们通常只能近似地进行推理,以得出一个近似的结果,这种推理方式也叫做似然推理。不过在模糊控制系统中已经发展出了一些比较固定的推理方法。
(1)Zadeh 推理
Zadeh 几乎发展出来了一套系统化的模糊控制理论,当然也包括模糊推理的理论化过程。
蕴含算子:
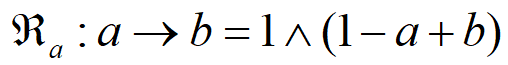
写成下面这个样子更容易理解:
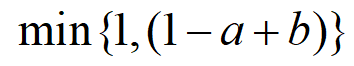
如果你不知道该如何理解“算子”两个字,没多大问题。学过传递函数得概念的话,你可以把算子理解为一个广义的传递函数,就是有个输入来的东西,通过与这个算子做运算,就可以得到你要的输出。其实本质上就是把一个映射单独拿了出来,就叫算子了。
(2)Mamdani 推理
Mandani推理简单粗暴,而且有效:
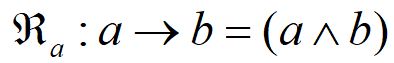
可以看到,在MATLAB的工具箱中,默认的就是他:
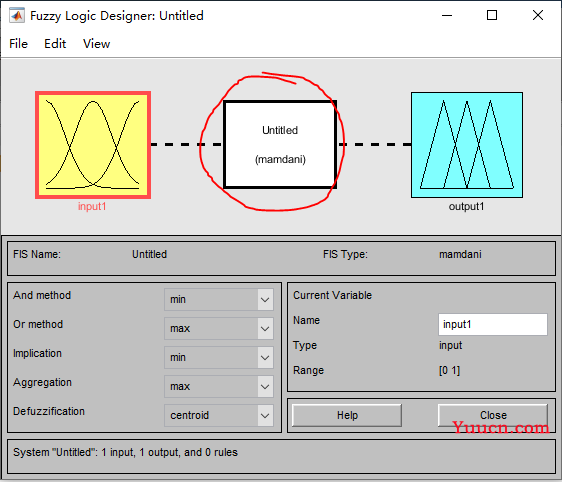
另外推理算法还有Baldwin、T’sukamato、Yager等推理算法。“通常把基于不精确的、不绝对可靠的或不完全的信息基础上的推理称为不确定性推理。同时,又把针对模糊系统的不确定性推理方法称为模糊推理方法。” 理解一下就是,在模糊系统中,基于不精确、不绝对可靠或信息不完全的推理就是模糊推理,也就是说,模糊推理本身上是无法做到完全准确的。注意啦,这是重点,这意味着我们可以把推理过程做到尽可能准确,那么用什么方法?—— 优化、神经网络…用你自己的办法。
4.解模糊化
解模糊化的主要目的就是将模糊控制系统得到的模糊输出值映射到真实的世界中,而不再以模糊语言的形式来表示。最直观的理解如:求“很大”这个模糊语言的数值是多少。解模糊化也叫“去模糊化”、“清晰化”等。
解模糊化最常用的几种方法:
(1)最大隶属度法
直接选择模糊输出中隶属度函数值最大的那个元素。
优点:主要信息突出,计算简单;
缺点:次要信息易丢失,方法粗糙,只适用于要求不高的模糊控制系统设计;
(2)中位数法(重心法、质心法、面积中心法)
目前最流行、合理的解模糊化方法。该方法将模糊控制系统中的中位数作为控制量。
优点:相比最大隶属度法,重心法包含了模糊子集中的所有信息;
缺点:计算复杂,尤其是在隶属度函数的论域为连续时,需要求解积分方程。
(3)加权平均法
适用于输出隶属度函数的模糊集是对称的。
相比重心法,计算相对简单。
(4)平均最大隶属度法
与最大隶属度法类似,但这里的最大隶属度值可以不是一个,而是多个。
(5)求和中心法
与加权平均法相似,但这里求和的是各个隶属度函数的面积,而加权平均的是隶属度函数值。
优点:计算速度很快。
(6)最大面积中心法
如果输出模糊集至少有两个凸的子区域,则最大面积凸子区域的重心作为输出的解模糊化值。
(7)首尾最大值法
三、模糊控制算法实例解析(含代码)
首先来看一个实例,控制进水阀S1和出水阀S2,使水箱水位保持在目标水位O处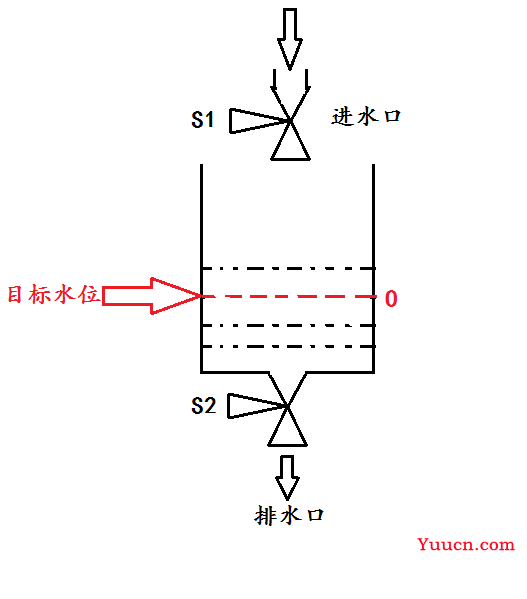
按照日常操作经验,有以下规则:
1、 若当前水位高于目标水位,则向外排水,差值越大,排水越快;
2、 若当前水位低于目标水位,则向内注水,差值越大,注水越快;
3、 若当前水位和目标水位相差很小,则保持排水速度和注水速度相等。
1、选择观测量和控制量
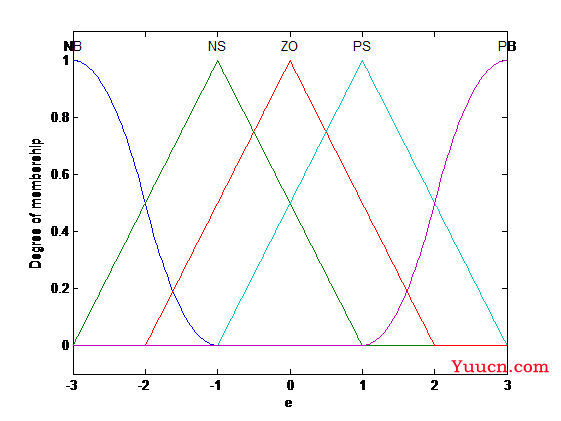
将偏差e划分为5个模糊集,负大(NB)、负小(NS)、零(ZO)、正小(PS)、正大(PB),e为负表示当前水位低于目标水位,e为正表示当前水位高于目标水位。设定e的取值范围为[-3,3],隶属度函数如下。
下面来设计一个模糊控制器
%水位模糊控制算法
clear all;
close all;
a = newfis('fuzzy tank');
a = addvar(a,'input','e',[-3,3]);
a = addmf(a,'input',1,'NB','zmf',[-3,-1]);
a =addmf(a,'input',1,'NS','trimf',[-3,-1,1]);
a =addmf(a,'input',1,'ZO','trimf',[-2,0,2]);
a =addmf(a,'input',1,'PS','trimf',[-1,1,3]);
a = addmf(a,'input',1,'PB','smf',[1,3]);
a = addvar(a,'output','u',[-4,4]);
a = addmf(a,'output',1,'NB','zmf',[-4,-2]);
a =addmf(a,'output',1,'NS','trimf',[-4,-2,0]);
a =addmf(a,'output',1,'ZO','trimf',[-2,0,2]);
a =addmf(a,'output',1,'PS','trimf',[0,2,4]);
a = addmf(a,'output',1,'PB','smf',[2,4]);
%建立模糊规则
rulelist=[1 1 1 1;
2 2 1 1;
3 3 1 1;
4 4 1 1;
5 5 1 1];
a = addrule(a,rulelist);
%设置反模糊化算法
a1 = setfis(a,'DefuzzMethod','mom');
writefis(a1,'tank');
a2 = readfis('tank');
figure(1);
plotfis(a2);
figure(2);
plotmf(a,'input',1);
figure(3);
plotmf(a,'output',1);
showrule(a);
ruleview('tank');
for i=1:1:7
e(i)=i-4;
Ulist(i)=evalfis([e(i)],a2);
end
Ulist = round(Ulist); %对决策结果四舍五入取整
disp('------------------------------------------------------');
disp('----------模糊控制表:e =[-3,3], u = [-4,4]-----------');
disp('------------------------------------------------------');
fprintf('| a |');
fprintf(' %d |',e);
fprintf('\n');
fprintf('| u |');
fprintf(' %d |',Ulist);
fprintf('\n');
参考
链接1
链接2