全连接层(Fully Connected layer,FC)
全连接层在整个卷积神经网络中起到了分类器的作用。如果说卷积层、池化层和激活函数等操作是将原始数据映射到隐层特征空间的话,全连接层则是起到了将学到的“分布式特征表示”映射到样本标记空间的作用。在 CNN 中,全连接常出现在最后几层,用于对前面设计的特征做加权和。
相邻层的所有神经元之间都有连接,称为全连接(fully connected)。用Affine层实现全连接层。在CNN结构中,经多个卷积层和池化层后,连接着1个或1个以上的全连接层。全连接层中的每个神经元与其前一层的所有神经元进行全连接,用来把前边提取到的特征综合起来。由于其全相连的特性,一般全连接层的参数也是最多的。为了提升 CNN网络性能,全连接层每个神经元的激活函数一般用ReLU函数。如下图所示
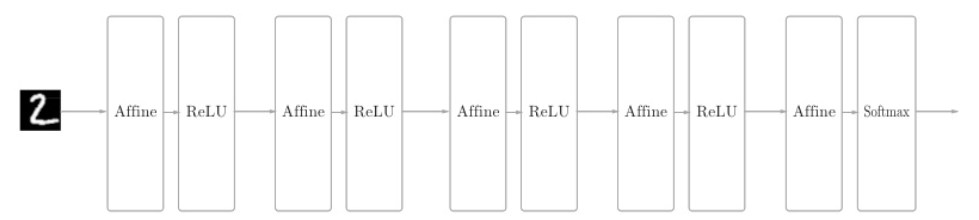
全连接的神经网络中,Affine层后面跟着激活函数ReLU层(或者Sigmoid层),图中堆叠了4层Affine-ReLU组合,然后第5层是Affine层,最后由Softmax层输出最终结果(概率)。
作用
-
全连接层主要用于线性映射,将输入数据从低维空间映射到高维空间。它也可以通过加入非线性激活函数来实现非线性映射。
复杂度
-
全连接层的复杂度很高,因为每个神经元与上一层的所有神经元都有连接。因此,当网络规模变大时,全连接层的计算量会呈指数增长。
全连接层的操作过程
卷积取的是局部特征,全连接就是把以前的局部特征重新通过权值矩阵组装成完整的图。因为用到了所有的局部特征,所以叫全连接。
如下图所示,一开始是9x9的图像,经过一系列的卷积、池化、激活函数操作后,即将进入到全连接层中。
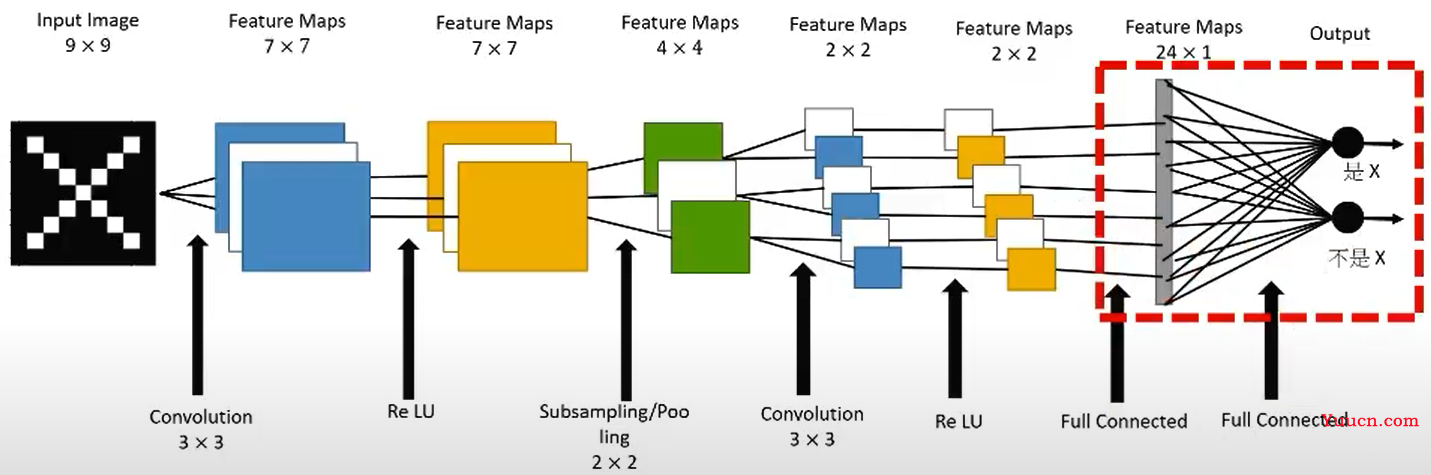
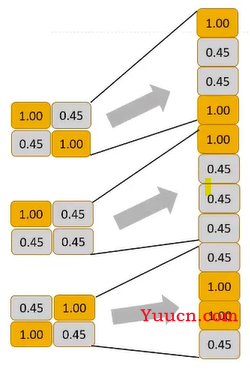
到了全连接层时,全连接层是一维数据,所以要将feature map变为一维。提问:它是怎么样把二维的输出,转换成一维形式的呢?假设在到达全连接层时是3个2x2的矩阵,此时这12×1向量中的每一个元素就是输入层的一个神经元,将这3个矩阵变为一维的操作如下图所示:
然后将得到的一维向量输入到网络中以概率(Softmax)的方式判断是X还是非X。粗线表示特征明显的数据,即是X的特征与不是X的特征,如下图所示:
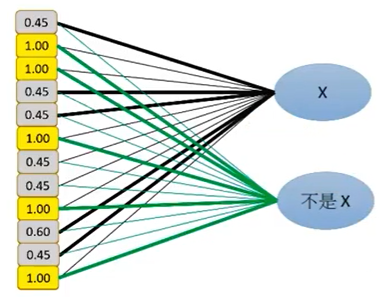
根据计算得到的权重矩阵,对其进行加权求和,就得到了每个分类的得分,然后根据softmax函数进行概率计算,得到X的概率为0.92,不是X的概率为0.5。如下图所示:
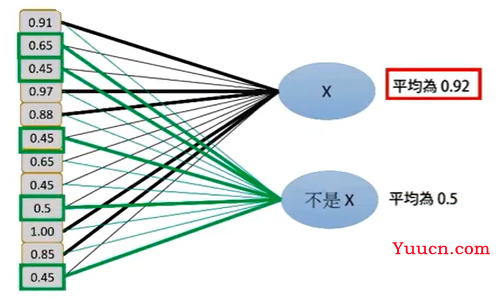
最终得到输出结果。
reference:
[1]:https://blog.csdn.net/m0_37407756/article/details/80904580
[2]:https://www.youtube.com/watch?v=_0rICtewveE
[3]:https://juejin.cn/post/7196330013981392933