前言
本文介绍了隐马尔可夫模型 (HMM)、最大熵马尔可夫模型 (MEMM) 和条件随机场 (CRF) 的比较分析。 HMM、MEMM 和 CRF 是三种流行的统计建模方法,通常应用于模式识别和机器学习问题。 让我们更详细地探讨每种方法。
一、隐马尔可夫模型 (HMM)
“隐藏”一词象征着只有系统发布的符号是可观察的,而用户无法查看状态之间的底层随机游走。 该领域的许多人将 HMM 视为有限状态机。
-
- HMM的优势
HMM 具有强大的统计基础和高效的学习算法,可以直接从原始序列数据中进行学习。 它允许以本地可学习方法的形式一致地处理插入和删除惩罚,并且可以处理可变长度的输入。 它们是序列概况最灵活的概括。 它还可以执行多种操作,包括多重对齐、数据挖掘和分类、结构分析和模式发现。 它也很容易组合到库中。
-
- HMM 的缺点
-
HMM 仅依赖于每个状态及其对应的观察对象:
-
序列标注,除了与单个词有关系外,还与观察到的序列长度、词上下文等方面有关。
-
目标函数和预测的目标函数不匹配:HMM得到的是状态和观测序列的联合分布P(Y, X),而在估计问题上,我们需要一个条件概率P(Y|X)。
二、最大熵马尔可夫模型 (MEMM)
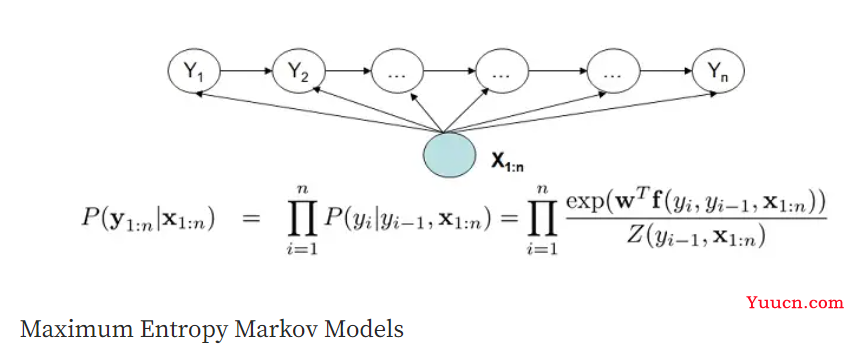
MEMM 考虑了相邻状态和整个观察序列之间的依赖关系,因此具有更好的表达能力。 MEMM不考虑P(X),减少建模工作量,学习目标函数与估计函数的一致性。
-
- MEMM 标签偏差
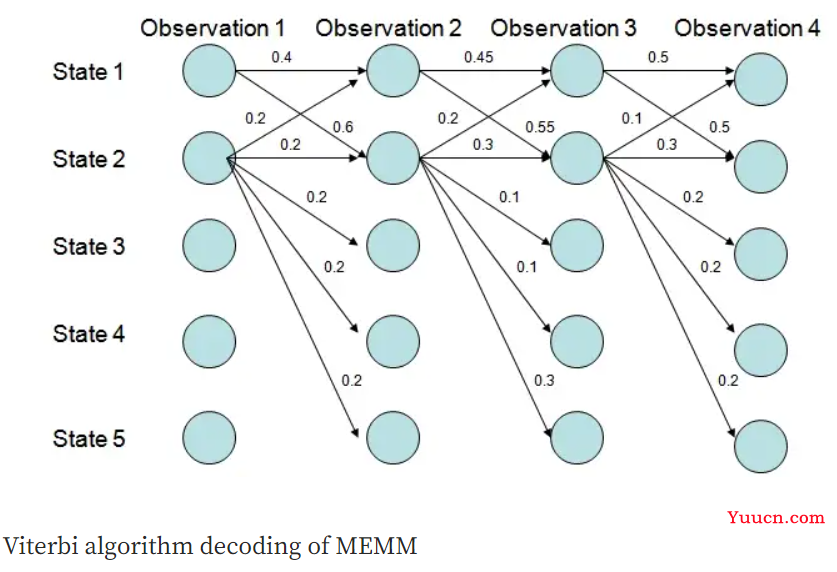
在上图 中,状态 1 倾向于转换为状态 2,同时状态 2 倾向于停留在状态 2。
P(1-> 1-> 1-> 1)= 0.4 x 0.45 x 0.5 = 0.09, P(2->2->2->2)= 0.2 x 0.3 x 0.3 = 0.018,
P(1->2->1->2)= 0.6 x 0.2x 0.5 = 0.06,P(1->1->2->2)= 0.4 x 0.55 x 0.3 = 0.066。
然而,最佳状态转换路径是 1 > 1 > 1 > 1。 为什么?
这是因为 State 2 的可转换状态比 State 1 多,从而降低了转换概率——MEMM 倾向于选择可转换状态较少的状态。 这种选择被称为标签偏差问题。 CRF 很好地解决了标签偏差问题。
三、条件随机场(CRF 模型)
CRF 模型解决了标注偏差问题,消除了 HMM 中两个不合理的假设。 当然,模型也变得更复杂了。MEMM采用局部方差归一化,CRF采用全局方差归一化。另一方面,MEMM 无法找到满足以下分布的相应参数,但是 CRF 可以:
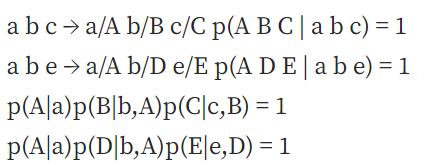
1.生成模型或判别模型
假设 o 是观测值,m 是模型。
a) 生成模型:无限样本>概率密度模型=生成模型>预测
如果你对 P(o|m) 建模,它就是一个生成模型。 其基本思想是,首先建立样本的概率密度模型,然后利用该模型进行推理预测。 样本无限大或尽可能大的要求是常识。 该方法借鉴了统计力学和贝叶斯理论。
HMM直接对转移概率和表型概率进行建模,计算共现概率。 因此,它是一个生成模型。
b) 判别模型:有限样本>判别函数=判别模型>预测
如果你在条件概率 P(m|o) 上建模,它就是判别模型。 其基本思想是以有限样本建立判别函数,不考虑样本的生成模型,直接研究预测模型。 其代表理论是统计学习理论。
CRF是一种判别模型。 MEMM 不是生成模型,而是基于状态分类的具有有限状态的模型。
2.拓扑结构
HMM和MEMM是有向图,而CRF是无向图。
3.全局最优或局部最优
HMM直接对转移概率和表型概率进行建模,计算共现概率。
MEMM 基于转移概率和表型概率建立共现概率。 它计算条件概率,只采用局部方差归一化,容易陷入局部最优。
CRF 在全局范围内计算归一化概率,而不是像 MEMM 那样在局部范围内计算。 它是一个最优的全局解决方案,解决了 MEMM 中的标签偏差问题。
4.CRF的优点和缺点
(1)优点
与HMM相比:由于CRF没有HMM那样严格的独立性假设,它可以容纳任何上下文信息。 其功能设计灵活(与ME相同)。
与MEMM相比:由于CRF计算的是全局最优输出节点的条件概率,因此克服了MEMM中label bias的弊端。
与ME相比:CRF计算的是在有待标记的观察序列时,整个标记序列的联合概率分布,而不是定义给定当前状态条件下下一个状态的状态分布。
(2)缺点
CRF 在算法的训练阶段具有高度的计算复杂性。 当更新的数据可用时,很难重新训练模型。
结论
这篇博客详细介绍了隐马尔可夫模型 (HMM)、最大熵马尔可夫模型 (MEMM) 和条件随机场 (CRF) 之间的比较分析。 在这篇文章中,我们明确了解到 CRF 和 MEMMS 主要是判别序列模型,而 HMM 主要是生成序列模型。 贝叶斯规则构成了 HMM 的基础。 相反,CRF 和 MEMM 基于过渡和可观察特征的 MaxEnt 模型。