1.极大极小值搜索介绍
人机博弈是人工智能的重要分支,人们在这一领域探索的过程中产生了大量的研究成果,而极小化极大算法(minimax)是其中最基础的算法,它由Shannon在1950年正式提出。
Minimax算法 又名极小化极大算法,是一种找出失败的最大可能性中的最小值的算法(即最小化对手的最大得益)。通常以递归形式来实现。极大极小搜索策略一般都是使用在一些博弈类的游戏之中。这样策略本质上使用的是深度搜索策略,所以一般可以使用递归的方法来实现。在搜索过程中,对本方有利的搜索点上应该取极大值,而对本方不利的搜索点上应该取极小值。极小值和极大值都是相对而言的。在搜索过程中需要合理的控制搜索深度,搜索的深度越深,效率越低,但是一般来说,走法越好。极大极小搜索可以分开写,也可以放在一起写。
在五子棋游戏中, AI 先获取当前所有可以下的位置(就是棋盘上的空格),然后每次在其中一个位置下子,根据棋型评估函数获取一个分数,所有位置都下过一遍后,从中获取评分最高的位置。这个就是极大值的搜索过程,我们称为 AI 的MAX层,即AI 要保证自己下棋的评分最大化。如果是轮到玩家下棋时,肯定会选取对自己最有利的位置,也可以说是对AI最不利的位置,即评分要最小化,我们称为AI的MIN层。上面是只有一层的搜索,如果要考虑多层搜索,第一层是AI下棋,第二层是玩家下棋,第三层是AI下棋,第四层是玩家下棋,依次类推。假设每一层有50个可选择的位置,每个位置看做树的一个节点,那么第一层是根节点下面的子节点,有50个节点,第二层是第一层下面的子节点,就有50×50个节点,第三层就有50×50×50个节点,依次类推,这样会形成一个巨大的博弈树。我们要做的就是搜索这棵树,找到对于AI最有利的下棋位置。假设一个两层的博弈树,如图1所示,最上面一层是树的根节点,这里MAX表示会选取下一层子节点中评分最高的。第二层的MIN表示会选取下一层子节点中评分最低的。第三层是叶子节点,只需要计算评分。注意:只有在叶子节点时才会计算评分,在树的中间层,对于AI来说暂时是无法知道哪一个节点是最有利的。
2.alpha beta剪枝介绍
Alpha-beta剪枝是一种搜索算法,用以减少极小化极大算法(Minimax算法)搜索树的节点数。这是一种对抗性搜索算法,主要应用于机器游玩的二人游戏(如井字棋、象棋、围棋)。当算法评估出某策略的后续走法比之前策略的还差时,就会停止计算该策略的后续发展。该算法和极小化极大算法所得结论相同,但剪去了不影响最终决定的分枝。 Alpha-beta剪枝的本质就是一种基于极小化极大算法的改进方法。在人机博弈中,双方回合制地进行走棋,己方考虑当自己在所有可行的走法中作出某一特定选择后,对方可能会采取的走法,从而选择最有利于自己的走法。
极大极小值搜索算法的缺点就是当博弈树的层数变大时,需要搜索的节点数目会指数级增长。比如上面每一层的节点为50时,六层博弈树的节点就是50的6次方,运算时间会非常漫长。
在上面的例子中,我们会计算所有叶子节点的评分,但这个不是必要的。Alpha-Beta剪枝就是用来将搜索树中不需要搜索的分支裁剪掉,以提高运算速度。基本的原理是:
当一个 MIN 层节点的 α值 ≤ β值时 ,剪掉该节点的所有未搜索子节点
当一个 MAX 层节点的 α值 ≥ β值时 ,剪掉该节点的所有未搜索子节点
其中α值是该层节点当前最有利的评分,β值是父节点当前的α值,根节点因为是MAX层,所以 β值 初始化为正无穷大(+∞)。
初始化节点的α值,如果是MAX层,初始化α值为负无穷大(-∞),这样子节点的评分肯定比这个值大。如果是MIN层,初始化α值为正无穷大(+∞),这样子节点的评分肯定比这个值小。
上述两个步骤的核心代码实现如下:
# 负极大值搜索 alpha+beta剪枝
def negativeMax(is_ai, depth, alpha, beta):
if is_GameOver(ai_list) or is_GameOver(me_list) or depth == 0:
return evaluation(is_ai)
# 未落子的位置
blank_list = list(set(all_list).difference(set(aime_list)))
blank_list = Rearrange(blank_list)
for next_step in blank_list:
global search_count
search_count += 1
if not has_neighbor(next_step):
continue
if is_ai:
ai_list.append(next_step)
else:
me_list.append(next_step)
aime_list.append(next_step)
value = -negativeMax(not is_ai, depth-1, -beta, -alpha)
if is_ai:
ai_list.remove(next_step)
else:
me_list.remove(next_step)
aime_list.remove(next_step)
if value > alpha:
if depth == DEPTH:
next_point[0], next_point[1] = next_step[0], next_step[1]
if value >= beta:
global cut_count
cut_count += 1
return beta
alpha = value
return alpha
def AI():
global cut_count
global search_count
# 剪枝次数
cut_count = 0
# 搜索次数
search_count = 0
negativeMax(True, DEPTH, -99999999, 99999999)
print('[Cut_Count]: %d, [Search_Count]: %d' % (cut_count, search_count))
return next_point[0], next_point[1]
3.展示结果
运行环境:python3.6.5
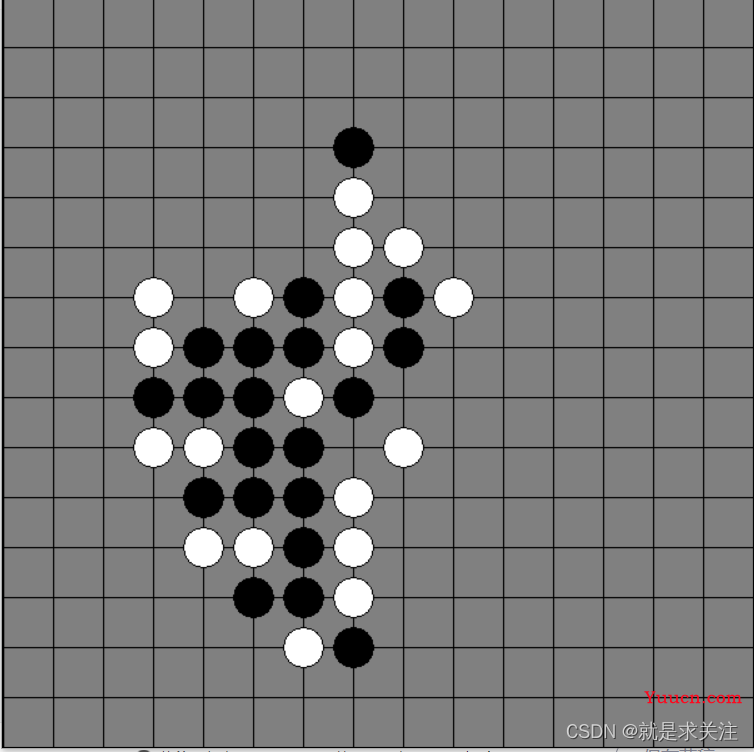
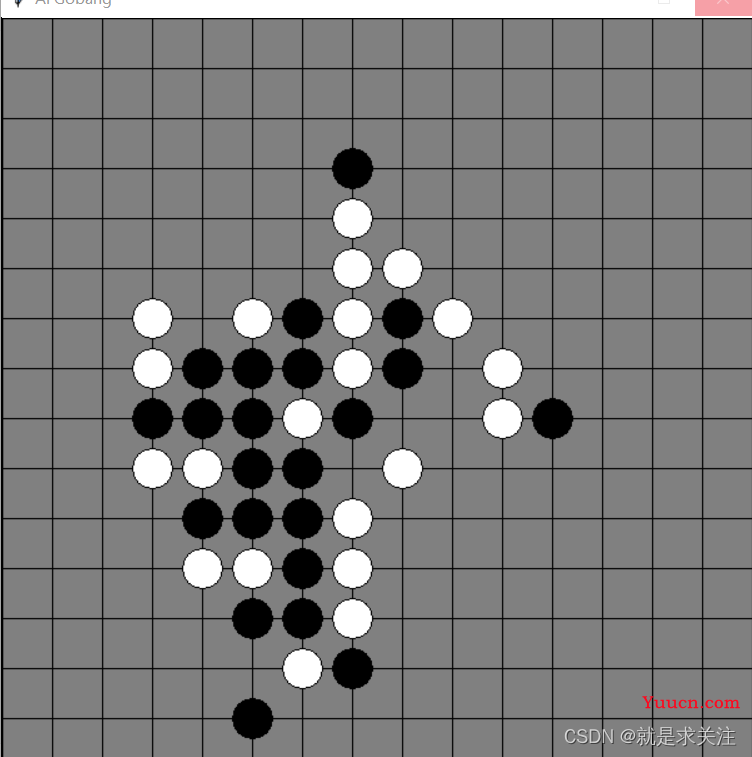
4.参考资料
1. Python 五子棋AI实现(3):极大极小值搜索和alpha beta剪枝_marble_xu的博客-CSDN博客_极大极小值算法实现五子棋
2.AI五子棋第二篇-运用极大极小值算法书写AI三子棋,可拓展到五子棋(建议收藏)_Ja_King_ZH的博客-CSDN博客_五子棋极大极小值
5. 全部代码下载
基于python的AI五子棋实现(极大极小值搜索和alphabeta剪枝)-机器学习文档类资源-CSDN下载