一、状态空间描述中两处噪声的理论假设
首先放出基本公式
状态方程:x(k) = Ax(k-1)+Bu(k-1)+w(k-1)
观测方程:y(k)=Cx(k)+v(k)
其中,w(k-1)为过程噪声,通常记作Q,v(k)为观测噪声,通常记作R。
标准卡尔曼滤波对于Q和R的要求主要有四点:
1.互不相关
2.零均值
3.高斯白噪声序列
4.Q,R分别是已知值的非负定阵和正定阵
也即:
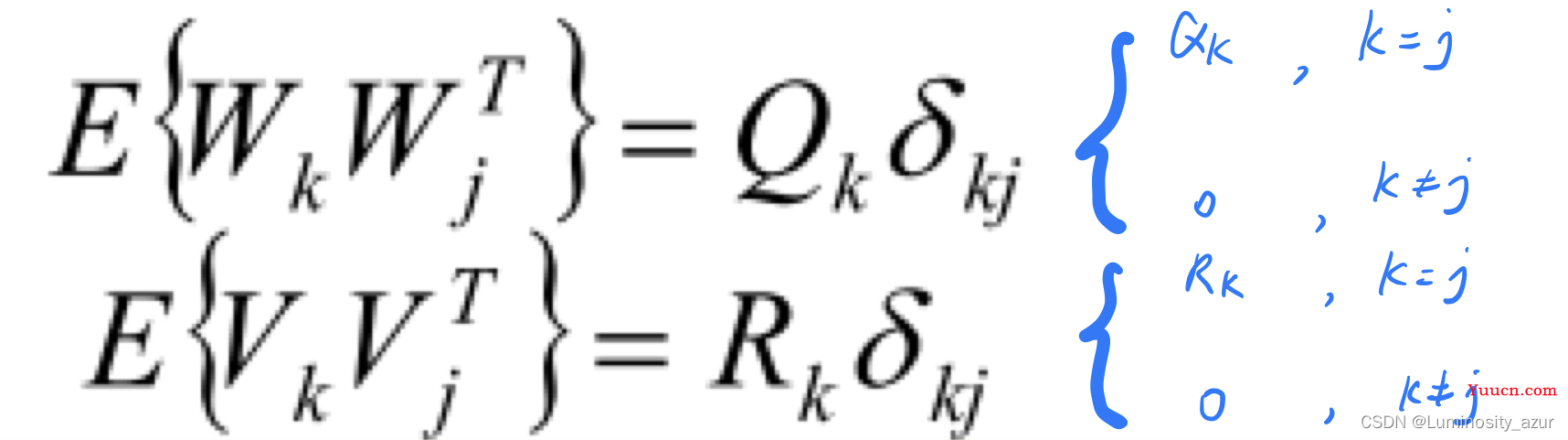
其中:

二、两处噪声如何从工程应用中获取
过程噪声Q:
构建所研究问题的“理想状态”,与实际情况进行对比实验,用所得的样本方差作为Q
例如研究滑块运动时,可以将在相对光滑表面的运动数据作为理想情况,与实际粗糙表面的情况进行对比;或是控制一个无人小车,在dt时间内,它其实是近圆弧行驶的,但我们研究时常常将它近似为线性模型了,因此产生的系统误差可以计算出一个范围阈值
观测噪声R:
这一噪声相对容易获取,通常依据传感器精度即可,直接进行观测实验,用样本方差作为Q
例如一个温度计的误差是±0.5,观测噪声R=0.5^2=0.25
三、两处噪声对于卡尔曼滤波估计误差的影响
事实上,我认为现阶段很难直接构建过程噪声Q和过程噪声R的具体数值与卡尔曼滤波估计的误差之间的线性关系,目前的研究主要集中在寻求Q和R的最优化组合
比如通过遗传算法来寻求这个最佳方差组合,可以参阅这篇文献:
[1]郭应时,王畅,张亚岐.噪声方差对卡尔曼滤波结果影响分析[J].计算机工程与设计,2014,35(02):641-645.DOI:10.16208/j.issn1000-7024.2014.02.016.
但需注意,在工程实际问题中,Q和R一定是客观存在的,我们尽力减小Q和R,通常更有助于我们获取更优的估计结果。