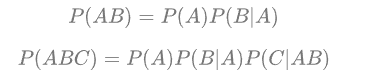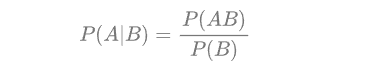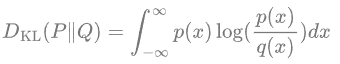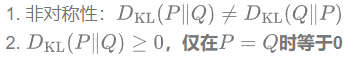发布时间：2023-04-19 文章分类：电脑百科投稿人：樱花字号：默认 | 大 | 超大打印

---

前言
一、常见生成模型
二、直观理解Diffusion model
三、形式化解析Diffusion model
*四、详解 Diffusion Model（数学推导）
- 1.前向过程(扩散过程)
- 2.逆扩散过程
- 3.逆扩散条件概率推导
- 4.训练损失
五、训练、测试伪代码
- 1. 训练
- 2.测试
六、代码解析
- 1.train_cifar.py
- 2.sample_images.py（预测过程）
总结

前言

AI 作画从 18 年的 DeepDream噩梦中惊醒过来，在 2022 年 OpenAI 的 DALL·E 2达到惊人效果，见图：

AI + 艺术涉及到 Transformer、VAE、ELBO、Diffusion Model 等一系列跟数学相关的知识。Diffusion Models 跟 VAE 一样原理很复杂。

扩散模型（论文：DDPM 即 Denoising Diffusion Probabilistic Model）2020年发表以来关注较少，因为他不像 GAN 那样简单粗暴好理解，但最近爆火以至于ICRL会议相关投稿一半以上，其最先进的两个文本生成图像——OpenAI 的 DALL·E 2 和 Google 的 Imagen，都是基于扩散模型来完成的。

一、常见生成模型

先横向对一下几个重要生成模型 GAN、VAE、Flow-based Models、Diffusion Models。

GAN 由一个生成器（generator）和判别器（discriminator）组成，generator 负责生成逼真数据以 “骗” 过 discriminator，而 discriminator 负责判断一个样本是真实的还是 “造” 出来的。GAN 的训练其实就是两个模型在相互学习，能不能不叫“对抗”，和谐一点。

VAE 同样希望训练一个生成模型 x=g(z)，这个模型能够将采样后的概率分布映射到训练集的概率分布，生成隐变量 z ，并且 z 是既含有数据信息又含有噪声，除了还原输入的样本数据以外，还可以用于生成新的数据。

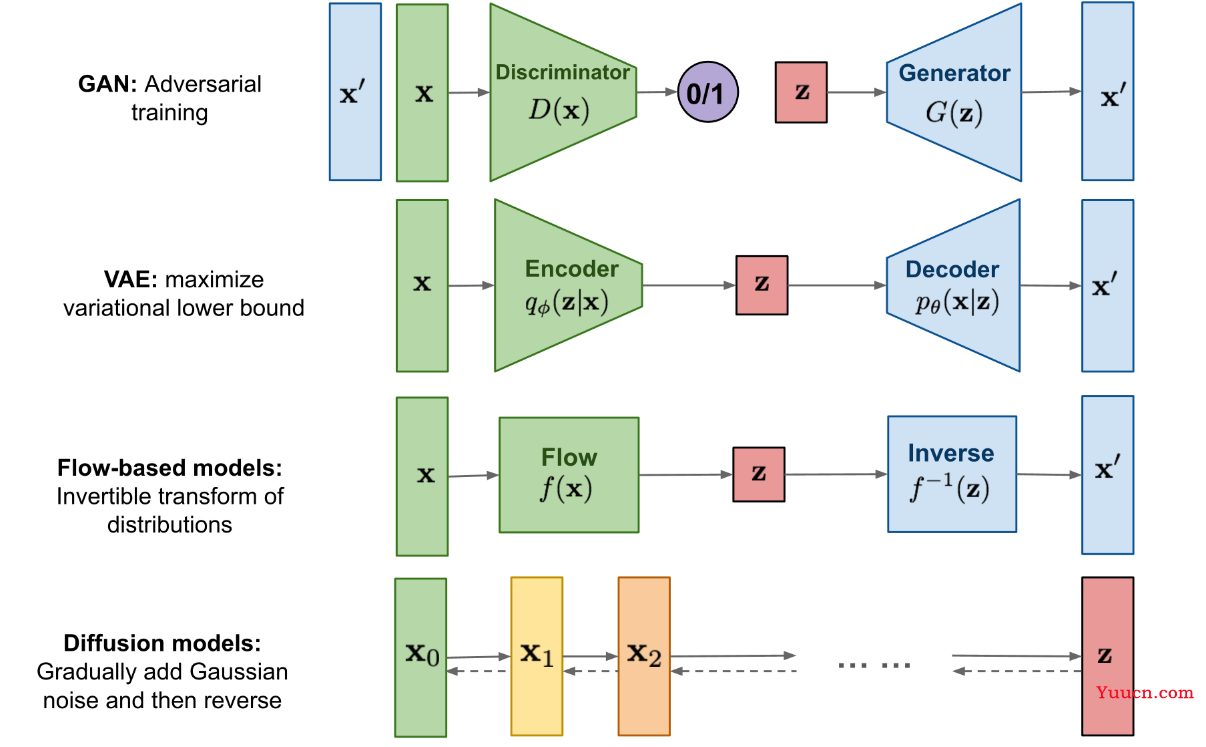
Diffusion Models 的灵感来自non-equilibrium thermodynamics （非平衡热力学）。理论首先定义扩散步骤的马尔可夫链，以缓慢地将随机噪声添加到数据中，然后学习逆向扩散过程以从噪声中构造所需的数据样本。与 VAE 或流模型不同，扩散模型是通过固定过程学习，并且隐空间 z 具有比较高的维度。

二、直观理解Diffusion model

生成式模型本质上是一组概率分布。如图所示，左边是一个训练数据集，里面所有的数据都是从某个数据 p_data 中独立同分布取出的随机样本。右边就是其生成式模型（概率分布），在这种概率分布中，找出一个分布 p_θ 使得它离的 p_data 距离最近。接着在 p_θ 上采新的样本，可以获得源源不断的新数据。

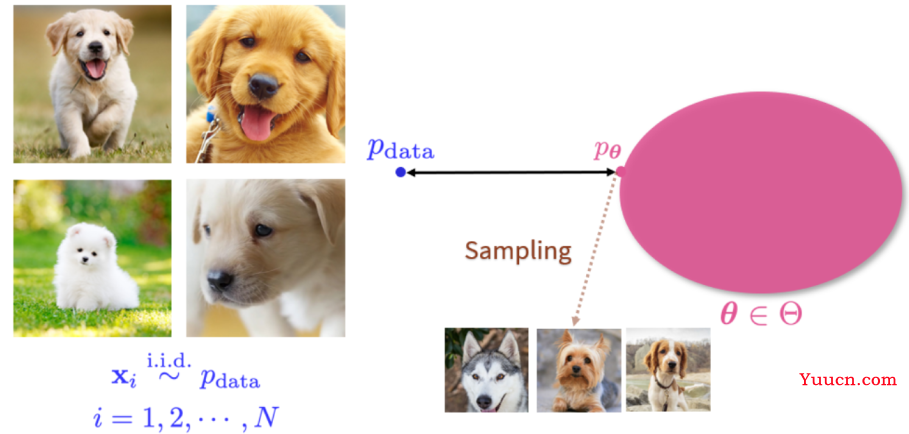
但是往往 p_data 的形式是非常复杂的，而且图像的维度很高，我们很难遍历整个空间，同时我们能观测到的数据样本也有限。

Diffusion作用：

我们可以将任意分布，当然也包括我们感兴趣的 p_data ，不断加噪声，使得他最终变成一个纯噪声分布 N(0,I)。怎么理解呢？

从概率分布的角度来看，考虑下图瑞士卷形状的二维联合概率分布 p(x,y) ，扩散过程q非常直观，本来集中有序的样本点，受到噪声的扰动，向外扩散，最终变成一个完全无序的噪声分布。

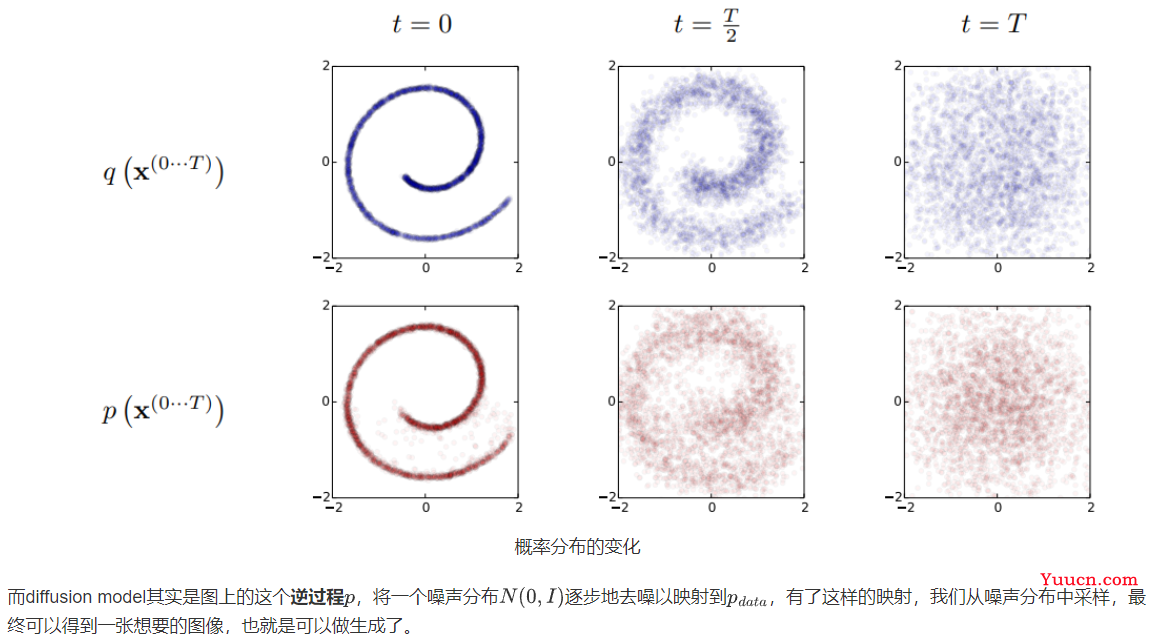
从单个图像样来看这个过程，扩散过程q就是不断往图像上加噪声直到图像变成一个纯噪声，逆扩散过程p就是从纯噪声生成一张图像的过程。样本变化：

三、形式化解析Diffusion model

既然叫生成模型，这意味着 Diffusion Models 用于生成与训练数据相似的数据。从根本上说，Diffusion Models 的工作原理，是通过连续添加高斯噪声来破坏训练数据，然后通过反转这个噪声过程，来学习恢复数据。

测试时，可以使用 Diffusion Models 将随机采样的噪声传入模型中，通过学习去噪过程来生成数据。也就是下面图中所对应的基本原理。

更具体地说，扩散模型是一种隐变量模型（latent variable model），使用马尔可夫链（Markov Chain, MC）映射到 latent space。通过马尔可夫链，在每一个时间步 t 中逐渐将噪声添加到数据 x_i 中以获得后验概率 q(x_1:T | x₀) ，其中 x₁…x_T 代表输入的数据同时也是 latent space。也就是说 Diffusion Models 的 latent space与输入数据具有相同维度。

后验概率：在贝叶斯统计中，一个随机事件或者一个不确定事件的后验概率（Posterior probability）是在考虑和给出相关证据或数据后所得到的条件概率。wiki

马尔可夫链为状态空间中经过从一个状态到另一个状态的转换的随机过程。该过程要求具备“无记忆”的性质：下一状态的概率分布只能由当前状态决定，在时间序列中它前面的事件均与之无关。

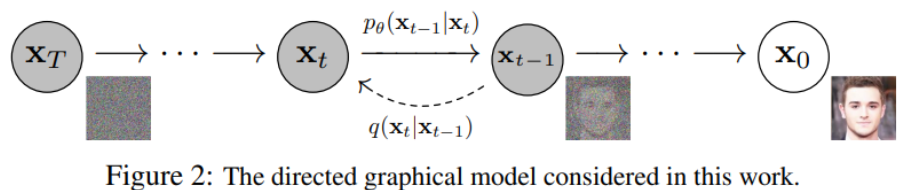
Diffusion Models 分为正向的扩散过程和反向的逆扩散过程。下图为扩散过程，从到最后的就是一个马尔可夫链，表示状态空间中经过从一个状态到另一个状态的转换的随机过程。而下标则是 Diffusion Models 对应的图像扩散过程。

最终，从 x₀ 输入的真实图像，经过 Diffusion Models 后被渐近变换为纯高斯噪声的图片 x_T 。

模型训练主要集中在逆扩散过程。训练扩散模型的目标是，学习正向的反过程：即训练概率分布 p_θ(x_t-1 | x_t) 。通过沿着马尔可夫链向后遍历，可以重新生成新的数据 x₀ 。

Diffusion Models 跟 GAN 或者 VAE 的最大区别在于不是通过一个模型来进行生成的，而是基于马尔可夫链，通过学习噪声来生成数据。

除了生成高质量图片之外呢，Diffusion Models 另一个好处是训练过程中没有对抗，对于 GAN 网络模型来说，对抗性训练其实是很不好调试的，因为对抗训练过程互相博弈的两个模型，对我们来说是个黑盒子。另外在训练效率方面，扩散模型还具有可扩展性和可并行性，那这里面如何加速训练过程，如何添加更多数学规则和约束，扩展到语音、文本、三维领域就很好玩了，可以出很多新文章。

*四、详解 Diffusion Model（数学推导）

上面已经清晰表示了 Diffusion Models 由正向过程（或扩散过程）和反向过程（或逆扩散过程）组成，其中输入数据逐渐被噪声化，然后噪声被转换回源目标分布的样本。原理即 马尔可夫链 + 条件概率分布。核心在于如何使用神经网络模型，来求解马尔可夫过程的概率分布。

1.前向过程(扩散过程)

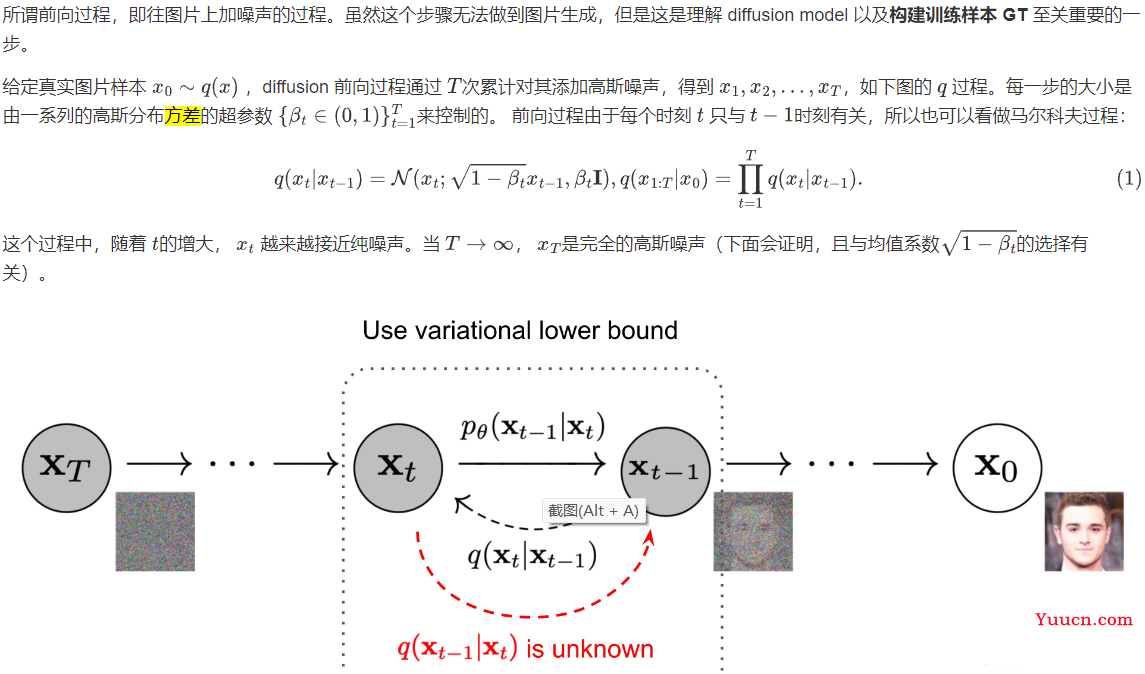
在实现和推导过程中要用到的两个重要特性：

特性 1：重参数（reparameterization trick）
重参数技巧在很多工作（gumbel softmax, VAE）中有所引用。如果我们要从某个分布中随机采样 (高斯分布) 一个样本，这个过程是无法反传梯度的。而这个通过高斯噪声采样得到 x_t 的过程在 diffusion 中到处都是，因此我们需要通过重参数技巧来使得他可微:

特性 2：任意时刻的 x_t 可以由 x₀ 和 β_t 表示

2.逆扩散过程

如果说前向过程 (forward) 是加噪的过程，那么逆向过程(reverse) 就是diffusion 的去噪推断过程。

如果我们能够逆转上述过程并从 q(x_t-1|x_t) 采样，就可以从高斯噪声 x_T ~N( 0, I )还原出原图分布 x₀ ~q(x) 。在文献7中证明了如果q(x_t|x_t-1) 满足高斯分布且 β_t 足够小， q(x_t-1|x_t) 仍然是一个高斯分布。然而我们无法简单推断 q(x_t-1|x_t) ，因此我们使用深度学习模型（参数为 θ，目前主流是 U-Net+attention 的结构）去预测这样的一个逆向的分布 p_θ（类似 VAE）：

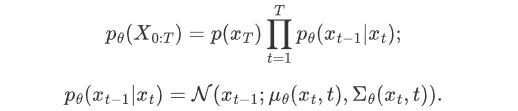
然而在论文中，作者把条件概率 p_θ(x_t-1|x_t) 的方差直接取了 β_t ，而不是上面说的需要网络去估计的 Σ_θ(x_t, t)，所以说实际上只有均值需要网络去估计。

正向扩散和逆扩散过程都是马尔可夫，然后正态分布，然后一步一步的条件概率，唯一的区别就是正向扩散里每一个条件概率的高斯分布的均值和方差都是已经确定的（依赖于 β_t 和 x₀），而逆扩散过程里面的均值和方差是我们网络要学出来。

3.逆扩散条件概率推导

虽然我们无法得到逆转过程的概率分布 q(x_t-1|x_t)，但是如果知道 x₀， q(x_t-1|x_t, x₀)就可以直接写出，这个玩意儿大概是这么个形式

贝叶斯公式：

带入公式得到：

7-1带入了贝叶斯公式2；7-2带入乘法公式1，再整理一下就能得到7-3

单变量正态分布概率密度函数定义为：
，代入得到式 7.4

式 7.5 可整理为 $\frac{1}{2}$ (ax²+bx+c）的形式，即 $\frac{1}{2}$ a (x+ $\frac{b}{2a}$ )²+C，其均值为- $\frac{b}{2a}$ ，方差为 $\frac{1}{a}$ ，因此稍加整理我们可以得到 (6) 中的方差和均值为：

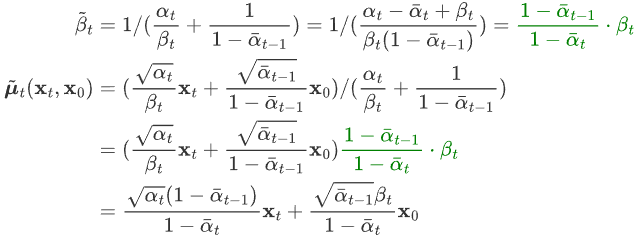
根据特性2的公式（2），我们得知，带入上式：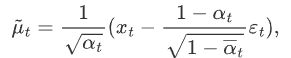

可以看出，在给定 x₀ 的条件下，后验条件高斯分布的均值只和超参数,x_t、ε_t 有关，方差只与超参数有关。

通过以上的方差和均值，我们就得到了q(x_t-1|x_t, x₀) 的解析形式。

4.训练损失

如何训练 Diffusion Models 以求得公式 (3) 中的均值 μ_θ(x_t，t) 和方差 Σ_θ (x_t，t) 呢？在 VAE 中我们学过极大似然估计的作用：对于真实的训练样本数据已知，要求模型的参数，可以使用极大似然估计。

统计学中，似然函数是一种关于统计模型参数的函数。给定输出x时，关于参数θ的似然函数L(θ|x)（在数值上）等于给定参数θ后变量X的概率：L(θ|x)=P(X=x|θ)。

Diffusion Models 通过极大似然估计，来找到逆扩散过程中马尔可夫链转换的概率分布，这就是 Diffusion Models 的训练目的。即最大化模型预测分布的对数似然，从Loss下降的角度就是最小化负对数似然：

这个过程很像VAE，即 可以使用变分下界(VLB)来优化负对数似然。

KL 散度是一种不对称统计距离度量，用于衡量一个概率分布 P 与另外一个概率分布 Q 的差异程度。连续分布的 KL 散度的数学形式是：

KL散度的性质：

由KL散度可知：

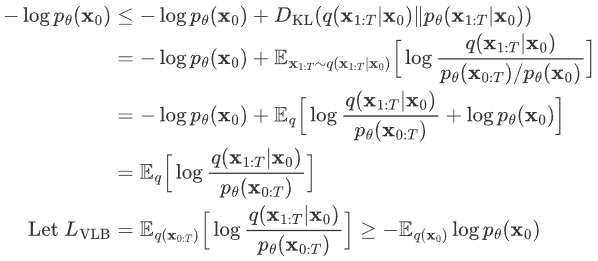
进一步可以写出上式的交叉熵的上界，进一步对其上界进行化简：

接下来我们对这三种情况进行分类讨论：

首先，由于前向过程 q 没有可学习参数，而 x_T 则是纯高斯噪声，因此 L_T 可以当做常量忽略。

然后，L_t-1 是KL散度，则可以看做拉近 2 个分布的距离：

第一个分布 q(x_t-1|x_T,x₀,) 我们已经在上一节推导出其解析形式，这是一个高斯分布，其均值和方差为
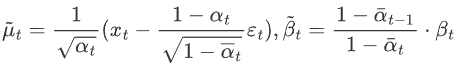
第二个分布 p_θ(x_t-1，x_t) 是我们网络期望拟合的目标分布，也是一个高斯分布，均值用网络估计，方差被设置为了一个和 β_t 有关的常数。

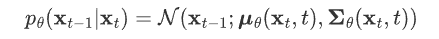
如果有两个分布 p,q 都是高斯分布，则他们的KL散度为

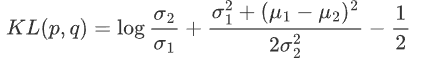
然后因为这两个分布的方差全是常数，和优化无关，所以其实优化目标就是两个分布均值的二范数

把这个公式，带入到上一公式中得到：

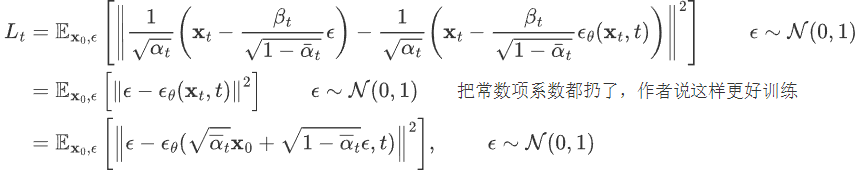
经过这样一番推导之后就是个 L2 loss。网络的输入是一张和噪声线性组合的图片，然后要估计出来这个噪声：

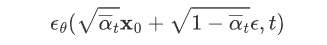
五、训练、测试伪代码

1. 训练

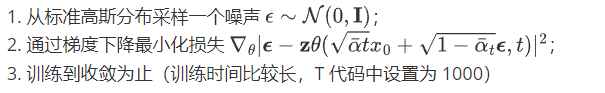
2.测试

六、代码解析

推荐一个简易ddpm项目，用cifar10数据集进行训练：
github.com/abarankab/DDPM
使用代码请见：

1.train_cifar.py

from torchvision import datasets
# 1.定义模型（Unet，后续会展开）
diffusion = script_utils.get_diffusion_from_args(args).to(device)
diffusion.load_state_dict(torch.load(args.model_checkpoint))  
# 2.迭代器
optimizer = torch.optim.Adam(diffusion.parameters(), lr=args.learning_rate)
# 3.从 torchvision 读入数据集
train_dataset = datasets.CIFAR10( root='./cifar_train', train=True,
            download=True, transform=script_utils.get_transform())
train_loader = script_utils.cycle(DataLoader( train_dataset,  batch_size=batch_size, shuffle=True, drop_last=True,num_workers=-1,))
for iteration in range(1, 80000):
        diffusion.train()
        x, y = next(train_loader)
        if args.use_labels:
            loss = diffusion(x, y)
        else:
            loss = diffusion(x)

展开1：定义 diffusion

model = UNet(img_channels=3, base_channels=128)
# 生成 t=1000 对应的 β（0.001~0.02）
if args.schedule == "cosine":
    betas = generate_cosine_schedule(args.num_timesteps=1000)
else:
    betas = generate_linear_schedule(num_timesteps=1000,
        1e-4 * 1000 / args.num_timesteps,
        0.02 * 1000 / args.num_timesteps)
diffusion = GaussianDiffusion( model, (32, 32), 3, 10, betas,
    ema_decay=0.9999,  ema_update_rate=1, ema_start=2000, loss_type='l2')
return diffusion

展开2：UNet
由 time_mlp、init_conv(3,128)、down（12层ResidualBlock）、mid、up（12层Res）组成。time_mlp为时间步 t 的可学习张量，下面有具体定义代码；
GaussianDiffusion为预设的一系列超参数，如 β、累乘α等：

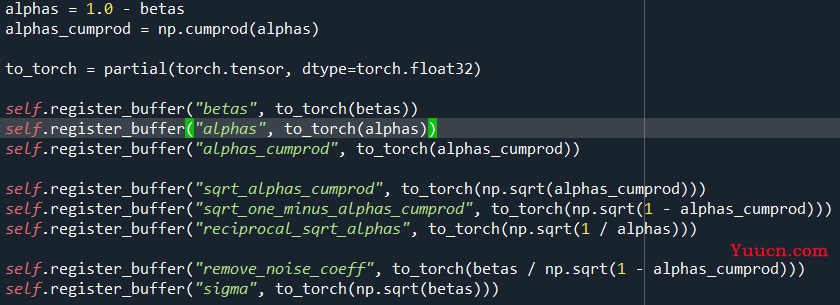
class PositionalEmbedding(nn.Module):
    __doc__ = r"""Computes a positional embedding of timesteps.
    Input:
        x: tensor of shape (N)
    Output:
        tensor of shape (N, dim)
    Args:
        dim (int): embedding dimension
        scale (float): linear scale to be applied to timesteps. Default: 1.0
    """
    def __init__(self, dim, scale=1.0):
        super().__init__()
        assert dim % 2 == 0
        self.dim = dim
        self.scale = scale
    def forward(self, x):
        device = x.device
        half_dim = self.dim // 2
        emb = math.log(10000) / half_dim
        emb = torch.exp(torch.arange(half_dim, device=device) * -emb)
        emb = torch.outer(x * self.scale, emb)
        emb = torch.cat((emb.sin(), emb.cos()), dim=-1)
        return emb
self.time_mlp = nn.Sequential(
            PositionalEmbedding(base_channels=128, time_emb_scale=1.0),
            nn.Linear(128, 512),
            nn.SiLU(),
            nn.Linear(512, 512),
        )

展开3：loss = diffusion(x)

b, c, h, w = x.shape                    # x:128，3，32，32  y是对应的128个标签
t = torch.randint(0, self.num_timesteps, (b,), device=device) 
# 从(0,1000)中随机选128个t
return self.get_losses(x, t, y)
def get_losses(self, x, t, y):
    noise = torch.randn_like(x)         # 随机噪声
    1.perturbed_x = self.perturb_x(x, t, noise)    
      # 用x0表示出xt， 下一行是具体操作：
      perturbed_x = extract(self.sqrt_alphas_cumprod, t, x.shape) * x + 
                    extract(self.sqrt_one_minus_alphas_cumprod, t, x.shape) * noise
    2.estimated_noise = self.model(perturbed_x, t, y)
      # 下一行是具体操作：
      2.1. time_emb = self.time_mlp(t)         # (128) -> (128,512)
           emb = math.log(10000) / half_dim    # 10000/64= 0.143
           emb = torch.exp(torch.arange(half_dim, device=device) * -emb)    # (64):[1.0, 0.86, 0.75, ...0.0001]
           emb = torch.outer(t * self.scale, emb)        # (128,64) 矩阵乘法
           emb = torch.cat((emb.sin(), emb.cos()), dim=-1)   # （128，128）
           time_emb = conv2d(emb)              # (128,512)
      2.2. for layer in self.downs:
               x = layer(x, time_emb, y)    # 将 time_emb 添加到特征中。即：
               out += self.time_bias(self.activation(time_emb))[:, :, None, None]
               # self.time_bias 是linear（512，128），activation 是silu函数。直接跟特征相加
           for layer in self.mid:
               x = layer(x, time_emb, y)
           for layer in self.ups:
               x = layer(x, time_emb, y)
           x = self.activation(self.out_norm(x))
           x = self.out_conv(x)              # 返回值为噪音（跟输入维度相同）
    if self.loss_type == "l1":
        loss = (estimated_noise - noise).abs().mean()
    elif self.loss_type == "l2":
        loss = (estimated_noise - noise).square().mean()
    return loss

2.sample_images.py（预测过程）

x = torch.randn(batch_size, self.img_channels, *self.img_size, device=device)
# 随机采样高斯噪声，作为xt
for t in range(self.num_timesteps - 1, -1, -1):        # T=1000
    t_batch = torch.tensor([t], device=device).repeat(batch_size)  
    x = self.remove_noise(x, t_batch, y, use_ema)      # 得到x(t-1),即：
    x = (    (x - extract(self.remove_noise_coeff, t, x.shape) * self.model(x, t, y)) 
         * extract(self.reciprocal_sqrt_alphas, t, x.shape)       )

最后一行代码，即

总结

Diffusion Model 通过参数化的方式表示为马尔科夫链，这意味着隐变量 x₁,…x_T 都满足当前时间步 t 只依赖于上一个时间步 t-1，这样对后续计算很有帮助。
马尔科夫链中的转变概率分布 p_θ(x_t-1|x_t) 服从高斯分布，在正向扩散过程当中高斯分布的参数是直接设定的，而逆向过程中的高斯分布参数是通过学习得到的。
Diffusion Model 网络模型扩展性和鲁棒性比较强，可以选择输入和输出维度相同的网络模型，例如类似于UNet的架构，保持网络模型的输入和输出 Tensor dims 相等。
Diffusion Model 的目的是对输入数据求极大似然函数，实际表现为通过训练来调整模型参数以最小化数据的负对数似然的变分上限
在概率分布转换过程中，因为通过马尔科夫假设，目标函数第4点中的变分上限都可以转变为利用 KL 散度来计算，因此避免了采用蒙特卡洛采样的方式。

标签 dd, 代码, 生成

【生成模型】DDPM概率扩散模型（原理+代码)

---

前言