智能优化算法:蜣螂优化算法
摘要:蜣螂优化算法( Dung beetle optimizer, DBO), 是由 Jiankai Xue 等于2022 年提出的一种群体智能优化算法。其灵感来源于蜣螂的生物行为过程,具有寻优能力强,收敛速度快的特点。
1.蜣螂优化算法
众所周知,蜣螂是自然界中一种常见的昆虫,动物的粪便为食,在全世界内分布广泛,扮演着自然界中分解者的角色,对生态系统平衡起着至关重要的作用。蜣螂有一个有趣的习惯,它们会把粪便捏成球,然后把它滚出来,目的是能够尽可能快速、有效地移动粪球,防止被其他蜣螂抢夺。蜣螂的可以利用天体线索(特别是太阳、月亮和偏振光)来导航,让粪球沿着直线滚动,如果完全没有光源(也就是在完全黑暗的环境中),蜣螂的就不再走直线,而是弯曲的,有时甚至略圆,有很多因素(如风、地面不平)都会导致蜣螂偏离原来的方向,蜣螂在滚粪球的过程如遇到障碍物而无法前进时,通常会爬到粪球上面"跳舞"(包括一系列的旋转和停顿),决定它们的运动方向。
从蜣螂的习性中观察发现,其获取粪球主要有以下两个目的:①用来产卵和养育下一代;②作为食物。蜣螂会把粪球埋起来,雌性蜣螂会在粪球里产卵,粪球不仅是蜣螂幼虫的发育场所,也是必需的食物。所以,粪球对蜣螂的生存起着不可替代的作用。
本位介绍了一种新的群体智能优化算法------DBO(Dung beetle optimizer)技术,其灵感主要来源于蜣螂的滚球、跳舞、觅食、偷窃、和繁殖等行为。
1.1 结构和算法
根据上面的讨论,蜣螂在滚动过程中需要通过天体线索导航,以保持粪球在直线路径上滚动。为了模拟滚球行为,要求蜣螂在整个搜索空间中沿着给定的方向移动。蜣螂的运动轨迹如图1所示。在图1中,蜣螂利用太阳来导航,其中红色箭头表示的是滚动的方向,同时,我们假设光源的强度也会影响蜣螂的路径。在滚动过程中,滚球蜣螂的位置更新,可以表示为
x
i
(
t
+
1
)
=
x
i
(
t
)
+
α
×
k
×
x
i
(
t
−
1
)
+
b
×
Δ
x
,
Δ
x
=
∣
x
i
(
t
)
−
X
w
∣
(1)
x_{i}(t + 1) = x_{i}(t) + \alpha \times k \times x_{i}(t - 1) + b \times \mathrm{\Delta}x,\\\mathrm{\Delta}x = \left| x_{i}(t) - X^{w} \right|\tag{1}
xi(t+1)=xi(t)+α×k×xi(t−1)+b×Δx,Δx=∣xi(t)−Xw∣(1)
其中,
t
t
t 表示当前迭代次数,
x
i
(
t
)
x_i(t)
xi(t) 表示第
i
i
i 只蜕螂在第
t
t
t 次迭代时的位置信息,
k
∈
(
,
0.2
]
k \in(0,0.2]
k∈(0,0.2] 表示挠度系数, 为定值。
b
b
b 表示属于
(
,
1
)
(0,1)
(0,1) 的定值,
α
\alpha
α 为自然系数, 赋值为
−
1
-1
−1 或
1
,
X
w
1, X^w
1,Xw 表示全局 最差位置,
Δ
x
\Delta x
Δx 用于模拟光强的变化。
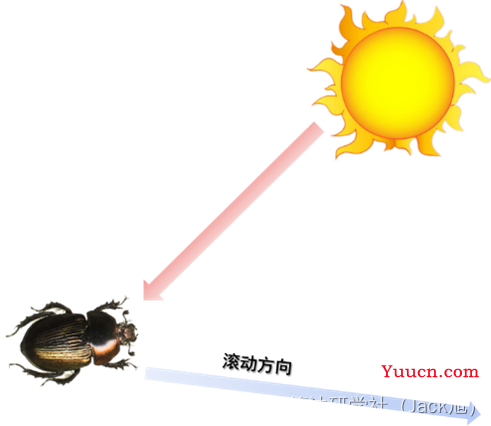
图1蜣螂运动轨迹的概念模型
在式(1)中, 适当选择两个参数
(
k
(k
(k 和
b
b
b )的值至关重要,
α
\alpha
α 代表诸多自然因素(如风和不平坦 的地面)可使蚝螂偏离原来的方向。当
α
=
1
\alpha=1
α=1 时, 表示无偏差, 当
α
=
−
1
\alpha=-1
α=−1 时, 表示偏离原方向。本 文中, 为模拟现实世界中的复杂环境, 通过概率法设
α
\alpha
α 为 1 或-1。同样,
Δ
x
\Delta x
Δx 的值越高表示光源 越弱, 同时,
k
k
k 和
b
b
b 分别设为
0.1
0.1
0.1 和
0.3
0.3
0.3 。利用
Δ
x
\Delta x
Δx 有以下两个优点: (1)算法在优化过程中, 可尽 可能地彻底地探索整个空间; (2)使算法具有更强的搜索性能, 从而避免陷入局部最优。
X
w
X^w
Xw 通 过控制
Δ
x
\Delta x
Δx 的值, 来扩大搜索范围。
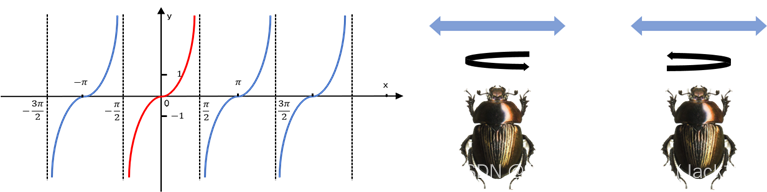
图2 切线函数的概念模型和蜣螂的舞蹈行为
当蛢螂遇到障碍物无法前进时, 就需要通过跳舞来重新定位, 目的是获得新的路线。为了 模拟舞蹈行为, 用切线函数得到新的滚动方向。需要指出的是, 只需要考虑定义在区间
[
,
π
]
[0, \pi]
[0,π], 如图 2 所示。一旦蜣螂成功确定了一个新的方向, 它继续把球向后㳖。因此, 将䖩螂的位置更 新, 并定义如下:
x
i
(
t
+
1
)
=
x
i
(
t
)
+
tan
θ
∣
x
i
(
t
)
−
x
i
(
t
+
1
)
∣
(2)
x_i(t+1)=x_i(t)+\tan \theta\left|x_i(t)-x_i(t+1)\right| \tag{2}
xi(t+1)=xi(t)+tanθ∣xi(t)−xi(t+1)∣(2)
其中,
θ
\theta
θ 为挠度角, 属于
[
,
π
]
[0, \pi]
[0,π] 。
∣
x
i
(
t
)
−
x
i
(
t
+
1
)
∣
\left|x_i(t)-x_i(t+1)\right|
∣xi(t)−xi(t+1)∣ 表示第
i
i
i 只蜕螂在第
t
t
t 次迭代时的位置与其 在第
t
−
1
t-1
t−1 次迭代时的位置之差。如果
θ
=
,
π
/
2
,
π
\theta=0, \pi / 2, \pi
θ=0,π/2,π, 蛢螂的位置不更新。
在自然界中, 粪球是被蛢螂滚到安全的地方藏起来。为了给它们的后代提供安全的环境, 选择合适的产卵地点对蚝螂来说至关重要。模拟䧳蚝螂产卵的区域边界选择策略, 其定义为:
L
b
∗
=
max
(
X
∗
×
(
1
−
R
)
,
L
b
)
,
U
b
∗
=
min
(
X
∗
×
(
1
+
R
)
,
U
b
)
(3)
\begin{aligned} & L b^*=\max \left(X^* \times(1-R), L b\right), \\ & U b^*=\min \left(X^* \times(1+R), \quad U b\right) \end{aligned}\tag{3}
Lb∗=max(X∗×(1−R),Lb),Ub∗=min(X∗×(1+R),Ub)(3)
其中,
X
∗
X^*
X∗ 为当前局部最佳位置,
L
b
∗
L b^*
Lb∗ 和
U
b
∗
U b^*
Ub∗ 分别为产卵区下限和上界,
R
=
1
−
t
/
T
max
,
T
max
R=1-t / T_{\max }, T_{\max }
R=1−t/Tmax,Tmax 表 示最大迭代次数,
L
b
L b
Lb 和
U
b
\mathrm{Ub}
Ub 分别代表优化问题的下界和上界。
如图 3 所示, 当前局部最佳位置
X
∗
X^*
X∗ 用一个大的棕色圈表示, 而
X
∗
X^*
X∗ 周围的小黑圈表示卵球。 每个卵球中都蕴含一枚蜣螂卵, 红色的小圆圈代表边界的上下界。
一旦确定了产卵区域, 雌性蜕螂就会选择这个区域的卵卵球产卵。对于 DBO 算法, 每只 雌蚝螂在每次迭代中只产一个卵。此外, 从式(3)中可以清楚地看到, 产卵区域的边界范围是 动态变化的, 这主要是由
R
R
R 值决定的。由此可见, 卵球的位置在迭代过程中也是动态的, 表示 为:
B
i
(
t
+
1
)
=
X
∗
+
b
1
×
(
B
i
(
t
)
−
L
b
∗
)
+
b
2
×
(
B
i
(
t
)
−
U
b
∗
)
(4)
B_i(t+1)=X^*+b_1 \times\left(B_i(t)-L b^*\right)+b_2 \times\left(B_i(t)-U b^*\right) \tag{4}
Bi(t+1)=X∗+b1×(Bi(t)−Lb∗)+b2×(Bi(t)−Ub∗)(4)
B
i
(
t
)
B_i(t)
Bi(t) 为第
t
\mathrm{t}
t 次迭代时第
i
\mathrm{i}
i 个卵球的位置信息,
b
1
b_1
b1 和
b
2
b_2
b2 表示大小为
1
×
D
1 \times \mathrm{D}
1×D 的两个独立随机向量,
D
\mathrm{D}
D 表示优化问题的维数。卵球的位置被严格限制在一定范围内。
一些已经长成成虫的蚝螂会从地下钻出来受食, 我们称它们为小蚝螂, 还需要建立最优受 食区域来引导蜣螂受食, 最佳受食区域的边界定义如下:
L
b
b
=
max
(
X
b
×
(
1
−
R
)
,
L
b
)
,
U
b
b
=
min
(
X
b
×
(
1
+
R
)
,
U
b
)
(5)
\begin{aligned} & L b^b=\max \left(X^b \times(1-R), \quad L b\right), \\ & U b^b=\min \left(X^b \times(1+R), \quad U b\right) \end{aligned} \tag{5}
Lbb=max(Xb×(1−R),Lb),Ubb=min(Xb×(1+R),Ub)(5)
X
b
X^b
Xb 表示全局最佳受食位置,
L
b
b
L b^b
Lbb 和乌
U
b
b
U b^b
Ubb 分别为最优受食区域的下界和上界, 其他参数在 式(3)中定义, 因此小蚝螂的位置更新如下:
x
i
(
t
+
1
)
=
x
i
(
t
)
+
C
1
×
(
x
i
(
t
)
−
L
b
b
)
+
C
2
×
(
x
i
(
t
)
−
U
b
b
)
(6)
x_i(t+1)=x_i(t)+C_1 \times\left(x_i(t)-L b^b\right)+C_2 \times\left(x_i(t)-U b^b\right) \tag{6}
xi(t+1)=xi(t)+C1×(xi(t)−Lbb)+C2×(xi(t)−Ubb)(6)
其中,
x
i
(
t
)
x_i(t)
xi(t) 表示第
t
t
t 次迭代时第
i
i
i 只小蚝螂的位置信息,
C
1
C_1
C1 表示一个服从正态分布的随机数,
C
2
C_2
C2 表示属于
(
,
1
)
(0,1)
(0,1) 的随机向量。
还有一些蚝螂被称为偷窃䖩螂, 会从其他蚝螂那里偷粪球,这是自然界中非常常见的现象。 从式(5)可以看出,
X
b
X^b
Xb 即最优的食物来源位置。因此, 我们可以假设
X
b
X^b
Xb 即表示争夺食物的最佳 地点。在迭代过程中, 偷穷槩螂的位置更新信息定义如下:
∣
x
i
(
t
+
1
)
=
X
b
+
S
×
g
×
(
∣
x
i
(
t
)
−
X
∗
∣
+
∣
x
i
(
t
)
−
X
b
∣
)
(7)
\mid x_i(t+1)=X^b+S \times g \times\left(\left|x_i(t)-X^*\right|+\left|x_i(t)-X^b\right|\right) \tag{7}
∣xi(t+1)=Xb+S×g×(∣xi(t)−X∗∣+∣∣xi(t)−Xb∣∣)(7)
其中,
x
i
(
t
)
x_i(t)
xi(t) 表示第
i
i
i 个偷窃蜕螂在第
t
t
t 次迭代时的位置信息,
g
g
g 是一个大小为
1
×
D
1 \times \mathrm{D}
1×D 维的随机向 量, 服从于正态分布,
S
S
S 表示恒定值。
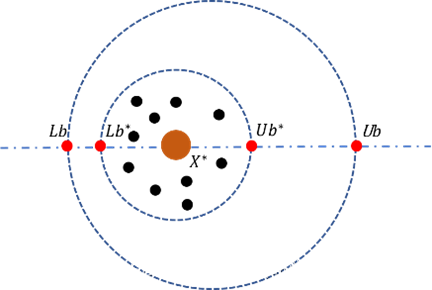
图3 边界选择策略的概念模型
偷窃蜣螂在优化过程中位置不断更新, 最后输出最佳位置
X
b
X^b
Xb 。根据此算法 更具体地说, 在
D
B
O
\mathrm{DBO}
DBO 算法中, 一个蜕螂种群包括
N
\mathrm{N}
N 种目标代理, 其中代理
i
i
i 都代表一组候选 解, 第
i
i
i 个代理的位置向量用
x
i
(
t
)
x_i(t)
xi(t) 表示,
x
i
(
t
)
=
(
x
i
1
(
t
)
,
x
i
2
(
t
)
,
…
…
,
x
i
D
(
t
)
)
x_i(t)=\left(x_{i 1}(t), x_{i 2}(t), \ldots \ldots, x_{i D}(t)\right)
xi(t)=(xi1(t),xi2(t),……,xiD(t)), 其中,
D
D
D 为搜索 空间的维数。它们的分布比例没有指定, 可以根据实际应用问题进行设置。
1.2 计算步骤
DBO 算法作为一种新颖的基于 SI 的优化技术, 主要有六个步骤:
(1) 初始化蜣螂群和 DBO 算法的参数;
(2) 根据目标函数计算出所有目标代理的适应度值;
(3) 更新所有蛲螂的位置;
(4) 判断每个目标代理是否超出边界;
(5) 更新当前最优解及其适应度值;
(6) 重复上述步骤, 直到 t 满足终止准则, 输出全局最优解及其适应度值。

2.实验结果
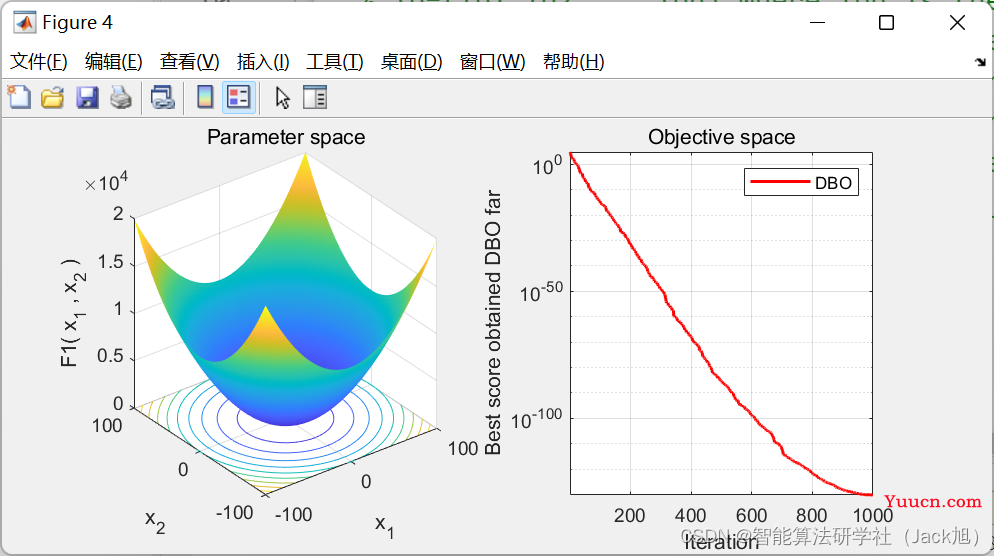
3.参考文献
[1] Jiankai Xue & Bo Shen (2022) Dung beetle optimizer: a new meta-heuristic algorithm for global optimization. The Journal of Supercomputing, DOI:10.1007/s11227-022-04959-6