本文内容

本文基于李宏毅老师对 Self-Attention 的讲解，进行理解和补充，并结合Pytorch代码，最终目的是使得自己和各位读者更好的理解Self-Attention

李宏毅Self-Attention链接: https://www.youtube.com/watch?v=hYdO9CscNes
PPT链接见视频下方

通过本文的阅读，你可以获得以下知识：

1. 什么是Self-Attention，为什么要用Self-Attention
2. Self-Attention是如何做的
3. Self-Attention是如何设计的
4. Self-Attention公式的细节
5. MultiHead Attention
6. Masked Attention

一、Self-Attention

1.1. 为什么要使用Self-Attention

假设现在一有个词性标注(POS Tags)的任务，例如：输入I saw a saw（我看到了一个锯子）这句话，目标是将每个单词的词性标注出来，最终输出为N, V, DET, N(名词、动词、定冠词、名词)。

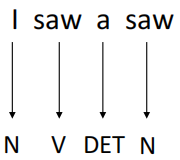
这句话中，第一个saw为动词，第二个saw(锯子)为名词。如果想做到这一点，就需要保证机器在看到一个向量(单词)时，要同时考虑其上下文，并且，要能判断出上下文中每一个元素应该考虑多少。例如，对于第一个saw，要更多的关注I，而第二个saw，就应该多关注a。

这个时候，就要Attention机制来提取这种关系：如果一个任务的输入是一个Sequence（一排向量），而且各向量之间有一定关系，那么就要利用Attention机制来提取这种关系。

1.2. 直观的感受下Self-Attention

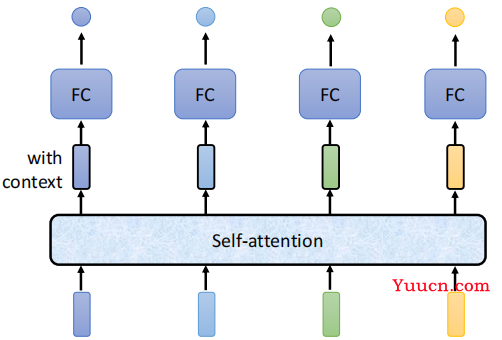
该图描述了Self-Attention的使用。Self-Attention接受一个Sequence（一排向量，可以是输入，也可以是前面隐层的输出），然后Self-Attention输出一个长度相同的Sequence，该Sequence的每个向量都充分考虑了上下文。 举个例子，输入是I、saw、a、saw，对应向量为：

I
=
[
1
]
,
  saw
=
[
1
]
,
  a
=
[
1
]
,
  saw
=
[
1
]
\text{I} = \begin{bmatrix} 1 \\ 0 \\ 0 \\ \end{bmatrix},~~\text{saw} = \begin{bmatrix} 0 \\ 1 \\ 0 \\ \end{bmatrix},~~\text{a} = \begin{bmatrix} 0 \\ 0 \\ 1 \\ \end{bmatrix},~~\text{saw} = \begin{bmatrix} 0 \\ 1 \\ 0 \\ \end{bmatrix}
I=​100​​,  saw=​010​​,  a=​001​​,  saw=​010​​

在经过Self-Attention层之后，可能就变成了这样：

I
′
=
[
0.7
0.28
0.02
]
,
  
saw
′
=
[
0.34
0.65
0.01
]
,
  
a
′
=
[
0.2
0.2
0.6
]
,
  
saw
′
=
[
0.01
0.5
0.49
]
\text{I}' = \begin{bmatrix} 0.7 \\ 0.28 \\ 0.02 \\ \end{bmatrix},~~\text{saw}' = \begin{bmatrix} 0.34 \\ 0.65 \\ 0.01 \\ \end{bmatrix},~~\text{a}' = \begin{bmatrix} 0.2 \\ 0.2 \\ 0.6 \\ \end{bmatrix},~~\text{saw}' = \begin{bmatrix} 0.01 \\ 0.5 \\ 0.49 \\ \end{bmatrix}
I′=​0.70.280.02​​,  saw′=​0.340.650.01​​,  a′=​0.20.20.6​​,  saw′=​0.010.50.49​​

对于第一个saw，它除了自身外，还要考虑 $0.34$个I；对于第二个saw，它要考虑$0.49$个a。

1.3. Self-Attenion是如何考虑上下文的

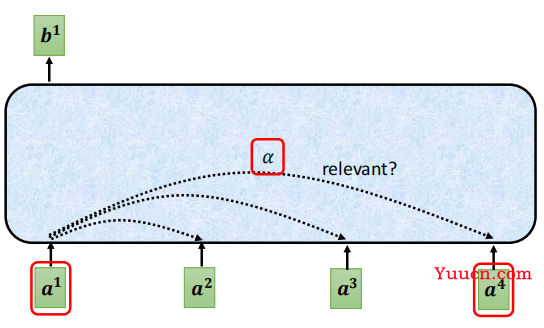
如图所示，每个输入都会和其他输入计算一个相关性分数，然后基于该分数，输出包含上下文信息的新向量。

对于上图，
a
1
a^1
a1需要与
a
1
,
a
2
,
a
3
,
a
4
a^1,a^2,a^3,a^4
a1,a2,a3,a4 分别计算相关性分数
α
1
,
1
,
α
1
,
2
,
α
1
,
3
,
α
1
,
4
\alpha_{1,1}, \alpha_{1,2}, \alpha_{1,3}, \alpha_{1,4}
α1,1​,α1,2​,α1,3​,α1,4​（需要和自己也计算一下）, $\alpha$ 的分数越高，表示两个向量的相关度越高。

计算好
α
1
,
∗
\alpha_{1,*}
α1,∗​ 后，就可以求出新的包含上下文信息的向量
b
1
b^1
b1，假设
α
1
,
1
=
5
,
α
1
,
2
=
2
,
α
1
,
3
=
1
,
α
1
,
4
=
2
\alpha_{1,1}=5, \alpha_{1,2}=2, \alpha_{1,3}=1, \alpha_{1,4}=2
α1,1​=5,α1,2​=2,α1,3​=1,α1,4​=2，则：

b
1
=
∑
i
α
1
,
i
⋅
a
i
=
5
⋅
a
1
+
2
⋅
a
2
+
1
⋅
a
3
+
2
⋅
a
4
b_1 = \sum_{i}\alpha_{1,i} \cdot a^i = 5 \cdot a^1 + 2 \cdot a^2 + 1 \cdot a^3 + 2 \cdot a^4
b1​=i∑​α1,i​⋅ai=5⋅a1+2⋅a2+1⋅a3+2⋅a4

同理，对于
b
2
b_2
b2​，首先计算权重
α
2
,
1
,
α
2
,
2
,
α
2
,
3
,
α
2
,
4
\alpha_{2,1}, \alpha_{2,2}, \alpha_{2,3}, \alpha_{2,4}
α2,1​,α2,2​,α2,3​,α2,4​ , 然后进行加权求和

如果按照上面这个式子做，还有两个问题：

1. $\alpha$ 之和不为1，这样会将输入向量放大或缩小
2. 直接用输入向量
   a
   i
   a^i
   ai去乘的话，拟合能力不够好

对于问题1，通常的做法是将 $\alpha$ 过一个Softmax（当然也可以选择其他的方式）

对于问题2，通常是将
a
i
a^i
ai 乘个矩阵（该矩阵是训练出来的），然后生成
v
i
v^i
vi ，然后用
v
i
v^i
vi 去乘 $\alpha$

1.4. 如何计算相关性分数 $\alpha$

首先，复习下向量相乘。两个向量相乘（做内积），公式为：$a\cdot b=|a||b|\cos \theta$ ， 通过公式可以很容易得出结论：

• 两个向量夹角越小（越接近），其内积越大，相关性越高。反之，两个向量夹角越大，相关性越差，如果夹角为90°，两向量垂直，内积为0，无相关性

通过上面的结论，很容易想到，要计算
a
1
a^1
a1 和
a
2
a^2
a2 的相关性，直接做内积即可，即
α
1
,
2
=
a
1
⋅
a
2
\alpha_{1,2} = a_1 \cdot a_2
α1,2​=a1​⋅a2​ 。 但如果直接这样，显然不好，例如，句子I saw a saw的saw和saw相关性一定很高(两个一样的向量夹角为0)，这样不就错了嘛。

为了解决上面这个问题，Self-Attention又额外“训练”了两个矩阵
W
q
W^q
Wq 和
W
k
W^k
Wk

• 
  W
  q
  W^q
  Wq 负责对“主角”进行线性变化，将其变换为 $q$，称为query，
• 
  W
  k
  W^k
  Wk 负责对“配角”进行线性变化，将其变换为 $k$，称为key

有了
W
q
和
W
k
W^q和W^k
Wq和Wk，我们就可以计算
a
1
a^1
a1 和
a
2
a^2
a2 的相关分数
α
1
,
2
\alpha_{1,2}
α1,2​了，即：

α
1
,
2
=
q
1
⋅
k
2
=
(
W
q
⋅
a
1
)
⋅
(
W
k
⋅
a
2
)
\alpha_{1,2} = q^1 \cdot k^2 = (W^q \cdot a^1 )\cdot (W^k \cdot a^2)
α1,2​=q1⋅k2=(Wq⋅a1)⋅(Wk⋅a2)

上面这些内容可以汇总成如下图：

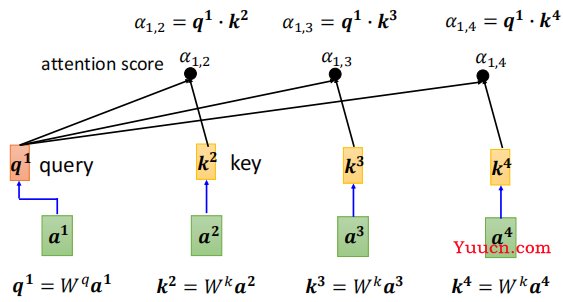
要计算
a
1
a^1
a1（主角）与
a
1
,
a
2
,
a
3
,
a
4
a^1, a^2, a^3, a^4
a1,a2,a3,a4（配角）的相关度，需要经历如下几步：

1. 通过
   W
   q
   W^q
   Wq ，计算
   q
   1
   q^1
   q1
2. 通过
   W
   k
   W^k
   Wk，计算
   k
   1
   ,
   k
   2
   ,
   k
   3
   ,
   k
   4
   k^1, k^2, k^3, k^4
   k1,k2,k3,k4
3. 通过 $q$ 和 $k$ ， 计算
   α
   1
   ,
   1
   ,
   α
   1
   ,
   2
   ,
   α
   1
   ,
   3
   ,
   α
   1
   ,
   4
   \alpha_{1,1}, \alpha_{1,2}, \alpha_{1,3}, \alpha_{1,4}
   α1,1​,α1,2​,α1,3​,α1,4​

上图并没有把
k
1
k^1
k1 画出来，但实际计算的时候，需要计算
k
1
k_1
k1​，即需要计算
a
1
a^1
a1和其自身的相关分数。

1.5. 将 $\alpha$ 归一化

还记得上面提到的，$\alpha$之和不为1，所以，在上面得到了
α
1
,
∗
\alpha_{1, *}
α1,∗​ 后，还需要过一下Softmax，将
α
1
,
∗
\alpha_{1, *}
α1,∗​进行归一化。如下图：

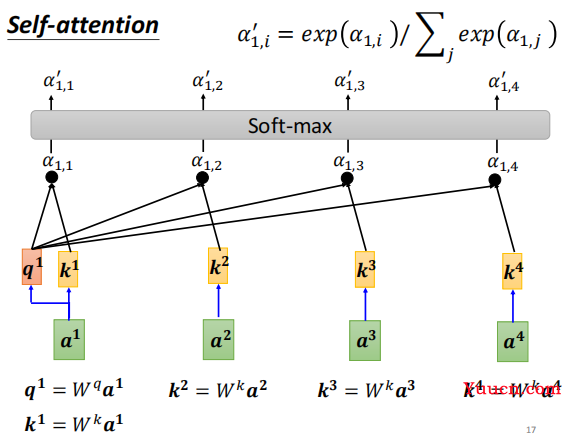
最终，会将归一化后的
α
1
,
∗
′
\alpha'_{1, *}
α1,∗′​ 作为
a
1
a^1
a1 与其它向量的相关分数。 同理，
a
2
,
a
3
,
.
.
.
a^2, a^3, ...
a2,a3,... 向量与其他向量的相关分数也这么求。

不一定非要用Softmax，你开心想用什么都行，说不定效果还不错，也不一定非要归一化。 只是通常是这么做的

1.6. 整合上述内容

求出了相关分数
α
′
\alpha '
α′，就可以进行加权求和计算出包含上下文信息的向量 $b$ 了。还记得上面提到过，如果直接用 $a$ 与
α
′
\alpha '
α′ 进行加权求和，泛化性不够好，所以需要对 $a$ 进行线性变换，得到向量 $v$，所以Self-Attention还需要训练一个矩阵
W
v
W^v
Wv 用于对 $a$ 进行线性变化，即：

v
1
=
W
v
⋅
a
1
        
v
2
=
W
v
⋅
a
2
         
v
3
=
W
v
⋅
a
3
           
v
4
=
W
v
⋅
a
4
v^1 = W^v \cdot a^1 ~~~~~~~~v^2 = W^v \cdot a^2~~~~~~~~~v^3 = W^v \cdot a^3~~~~~~~~~~~v^4 = W^v \cdot a^4
v1=Wv⋅a1        v2=Wv⋅a2         v3=Wv⋅a3           v4=Wv⋅a4

然后就可用 $v$ 与
α
′
\alpha '
α′ 进行加权求和，得到 $b$ 了。

b
1
=
∑
i
α
1
,
i
′
⋅
v
i
=
α
1
,
1
′
⋅
v
1
+
α
1
,
2
′
⋅
v
2
+
α
1
,
3
′
⋅
v
3
+
α
1
,
4
′
⋅
v
4
b^1 = \sum_i \alpha'_{1,i} \cdot v^i = \alpha'_{1,1} \cdot v^1 + \alpha'_{1,2} \cdot v^2 + \alpha'_{1,3} \cdot v^3 + \alpha'_{1,4} \cdot v^4
b1=i∑​α1,i′​⋅vi=α1,1′​⋅v1+α1,2′​⋅v2+α1,3′​⋅v3+α1,4′​⋅v4

将求
b
1
b^1
b1 的整个过程可以归纳为下图：

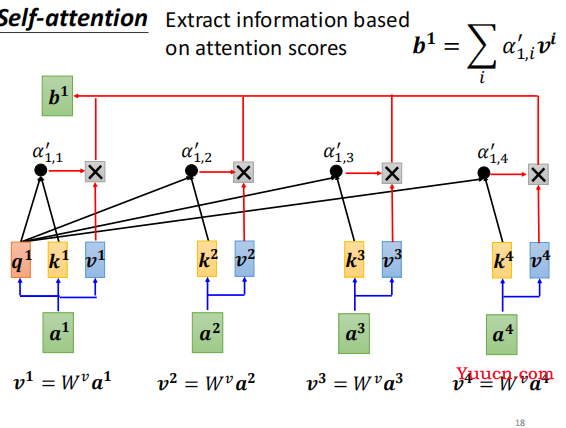
用更正式的话描述一下整个过程：

有一组输入序列
I
=
(
a
1
,
a
2
,
⋯
 
,
a
n
)
I = (a^1, a^2, \cdots, a^n)
I=(a1,a2,⋯,an)，其中
a
i
a^i
ai 为向量， 将序列 $I$ 通过Self-Attention，可以将其转化为另外一个序列
O
=
(
b
1
,
b
2
,
⋯
 
,
b
n
)
O = (b^1, b^2, \cdots, b^n)
O=(b1,b2,⋯,bn)，其中向量
b
i
b^i
bi 是由向量
a
i
a^i
ai 结合其上下文得出的，
b
i
b^i
bi 的求解过程如下：

1. 求出查询向量
   q
   i
   q^i
   qi， 公式为
   q
   i
   =
   W
   q
   ⋅
   a
   i
   q^i = W^q \cdot a^i
   qi=Wq⋅ai
2. 求出
   k
   1
   ,
   k
   2
   ,
   ⋯
    
   ,
   k
   n
   k^1,k^2, \cdots, k^n
   k1,k2,⋯,kn，公式为
   k
   j
   =
   W
   k
   ⋅
   a
   j
   k^j = W^k \cdot a^j
   kj=Wk⋅aj
3. 求出
   α
   i
   ,
   1
   ,
   α
   i
   ,
   2
   ,
   ⋯
    
   ,
   α
   i
   ,
   n
   \alpha_{i,1}, \alpha_{i,2}, \cdots, \alpha_{i,n}
   αi,1​,αi,2​,⋯,αi,n​ ， 公式为
   α
   i
   ,
   j
   =
   q
   i
   ⋅
   k
   j
   \alpha_{i,j}=q^i\cdot k^j
   αi,j​=qi⋅kj
4. 将
   α
   i
   ,
   1
   ,
   α
   i
   ,
   2
   ,
   ⋯
    
   ,
   α
   i
   ,
   n
   \alpha_{i,1}, \alpha_{i,2}, \cdots, \alpha_{i,n}
   αi,1​,αi,2​,⋯,αi,n​ 进行归一化得到
   α
   i
   ,
   1
   ′
   ,
   α
   i
   ,
   2
   ′
   ,
   ⋯
    
   ,
   α
   i
   ,
   n
   ′
   \alpha'_{i,1}, \alpha'_{i,2}, \cdots, \alpha'_{i,n}
   αi,1′​,αi,2′​,⋯,αi,n′​，公式为
   α
   i
   ,
   j
   ′
   =
   Softmax
   (
   α
   i
   ,
   j
   ;
   α
   i
   ,
   ∗
   )
   =
   exp
   ⁡
   (
   α
   i
   ,
   j
   )
   /
   ∑
   t
   exp
   ⁡
   (
   α
   i
   ,
   t
   )
   \alpha'_{i,j} = \text{Softmax}(\alpha_{i,j};\alpha_{i,*}) = \exp(\alpha_{i,j})/\sum_t \exp(\alpha_{i,t})
   αi,j′​=Softmax(αi,j​;αi,∗​)=exp(αi,j​)/∑t​exp(αi,t​)
5. 求出向量
   v
   1
   ,
   v
   2
   ,
   ⋯
    
   ,
   v
   n
   v^1, v^2, \cdots, v^n
   v1,v2,⋯,vn， 公式为：
   v
   j
   =
   W
   v
   ⋅
   a
   j
   v^j=W^v \cdot a^j
   vj=Wv⋅aj
6. 求出
   b
   i
   b^i
   bi， 公式为
   b
   i
   =
   ∑
   j
   α
   i
   ,
   j
   ′
   ⋅
   v
   j
   b^i = \sum_j \alpha'_{i,j} \cdot v^j
   bi=∑j​αi,j′​⋅vj

其中，
W
q
,
W
k
,
W
v
W^q, W^k, W^v
Wq,Wk,Wv 都是训练出来的

到这里Self-Attention的面纱已经揭开，但还没有结束，因为上面的步骤如果写成代码，需要大量的for循环，显然效率太低，所以需要进行向量化，能合并成向量的合成向量，能合并成矩阵的合成矩阵。

1.7. 向量化

向量$a$ 的矩阵化，假设列向量
a
i
a^i
ai 维度为 $d$，显然可以将输入转化为矩阵 $I$，公式为：

I
d
×
n
=
(
a
1
,
a
2
,
⋯
 
,
a
n
)
I_{d\times n} = (a^1, a^2, \cdots, a^n)
Id×n​=(a1,a2,⋯,an)

接下来定义
W
q
,
W
k
,
W
v
W^q, W^k, W^v
Wq,Wk,Wv 矩阵，其中
W
q
W^q
Wq和
W
k
W^k
Wk的矩阵维度必须一致，为
d
k
×
d
d_k\times d
dk​×d，而
W
v
W^v
Wv的矩阵维度为
d
v
×
d
d_v\times d
dv​×d，其中 $d_k $和
d
v
d_v
dv​ 都是需要调的超参数（一般与词向量的维度 $d$ 保持一致）。
d
k
d_k
dk​ 只影响过程，但
d
v
d_v
dv​ 会影响结果，即
d
v
d_v
dv​ 是Attention的输出向量 $b$ 的维度。 定义好
W
q
W^q
Wq 的维度后，就可以将 $q$ 矩阵化了，

向量 $q$ 的矩阵化，公式为：

Q
d
k
×
n
=
(
q
1
,
q
2
,
⋯
 
,
q
n
)
=
W
d
k
×
d
q
⋅
I
d
×
n
Q_{d_k\times n} = (q^1, q^2, \cdots, q^n) = W^q_{d_k\times d} \cdot I_{d\times n}
Qdk​×n​=(q1,q2,⋯,qn)=Wdk​×dq​⋅Id×n​

同理，向量k的矩阵化，公式为：

K
d
k
×
n
=
(
k
1
,
k
2
,
⋯
 
,
k
n
)
=
W
k
⋅
I
K_{d_k\times n} = (k^1, k^2, \cdots, k^n) = W^k \cdot I
Kdk​×n​=(k1,k2,⋯,kn)=Wk⋅I

同理，向量v的矩阵化，公式为：

V
d
v
×
n
=
(
v
1
,
v
2
,
⋯
 
,
v
n
)
=
W
v
⋅
I
V_{d_v\times n} = (v^1, v^2, \cdots, v^n) = W^v \cdot I
Vdv​×n​=(v1,v2,⋯,vn)=Wv⋅I

得到了矩阵$Q$和$K$，那么就很容易得出相关分数 $\alpha$ 的矩阵了，

相关分数 $\alpha$ 的矩阵为：

A
n
×
n
=
[
α
1
,
1
α
2
,
1
⋯
α
n
,
1
α
1
,
2
α
2
,
2
⋯
α
n
,
2
⋮
⋮
⋮
α
1
,
n
α
2
,
n
⋯
α
n
,
n
]
=
K
T
⋅
Q
=
[
k
1
T
k
2
T
⋮
k
n
T
]
⋅
(
q
1
,
q
2
,
⋯
 
,
q
n
)
A_{n\times n} = \begin{bmatrix} \alpha_{1,1} & \alpha_{2,1} & \cdots &\alpha_{n,1} \\ \alpha_{1,2} & \alpha_{2,2} & \cdots &\alpha_{n,2} \\ \vdots & \vdots & &\vdots \\ \alpha_{1,n} & \alpha_{2,n} & \cdots &\alpha_{n,n} \\ \end{bmatrix} = K^T \cdot Q =\begin{bmatrix} {k^1}^T \\ {k^2}^T \\ \vdots \\ {k^n}^T \end{bmatrix} \cdot (q^1, q^2, \cdots, q^n)
An×n​=​α1,1​α1,2​⋮α1,n​​α2,1​α2,2​⋮α2,n​​⋯⋯⋯​αn,1​αn,2​⋮αn,n​​​=KT⋅Q=​k1Tk2T⋮knT​​⋅(q1,q2,⋯,qn)

我的定义
k
i
k^i
ki 是列向量，所以要转置一下

进一步，
α
′
\alpha '
α′ 的矩阵为：

A
n
×
n
′
=
softmax
(
A
)
=
[
α
1
,
1
′
α
2
,
1
′
⋯
α
n
,
1
′
α
1
,
2
′
α
2
,
2
′
⋯
α
n
,
2
′
⋮
⋮
⋮
α
1
,
n
′
α
2
,
n
′
⋯
α
n
,
n
′
]
A'_{n\times n} = \textbf{softmax}(A) = \begin{bmatrix} \alpha'_{1,1} & \alpha'_{2,1} & \cdots &\alpha'_{n,1} \\ \alpha'_{1,2} & \alpha'_{2,2} & \cdots &\alpha'_{n,2} \\ \vdots & \vdots & &\vdots \\ \alpha'_{1,n} & \alpha'_{2,n} & \cdots &\alpha'_{n,n} \\ \end{bmatrix}
An×n′​=softmax(A)=​α1,1′​α1,2′​⋮α1,n′​​α2,1′​α2,2′​⋮α2,n′​​⋯⋯⋯​αn,1′​αn,2′​⋮αn,n′​​​

A
′
A'
A′ 有了，$V$ 有了，那就可以对输出向量 $b$ 进行矩阵化了，

输出向量b的矩阵化，公式为：

O
d
v
×
n
=
(
b
1
,
b
2
,
⋯
 
,
b
n
)
=
V
d
v
×
n
⋅
A
n
×
n
′
=
(
v
1
,
v
2
,
⋯
 
,
v
n
)
⋅
[
α
1
,
1
′
α
2
,
1
′
⋯
α
n
,
1
′
α
1
,
2
′
α
2
,
2
′
⋯
α
n
,
2
′
⋮
⋮
⋮
α
1
,
n
′
α
2
,
n
′
⋯
α
n
,
n
′
]
O_{d_v\times n} = (b^1, b^2, \cdots, b^n) = V_{d_v\times n} \cdot A'_{n\times n} = (v^1, v^2, \cdots, v^n) \cdot \begin{bmatrix} \alpha'_{1,1} & \alpha'_{2,1} & \cdots &\alpha'_{n,1} \\ \alpha'_{1,2} & \alpha'_{2,2} & \cdots &\alpha'_{n,2} \\ \vdots & \vdots & &\vdots \\ \alpha'_{1,n} & \alpha'_{2,n} & \cdots &\alpha'_{n,n} \\ \end{bmatrix}
Odv​×n​=(b1,b2,⋯,bn)=Vdv​×n​⋅An×n′​=(v1,v2,⋯,vn)⋅​α1,1′​α1,2′​⋮α1,n′​​α2,1′​α2,2′​⋮α2,n′​​⋯⋯⋯​αn,1′​αn,2′​⋮αn,n′​​​

将上面全部整合起来，就可以的到，整合后的公式为

O
=
Attention
(
Q
,
K
,
V
)
=
V
⋅
softmax
(
K
T
Q
)
O = \textbf{Attention}(Q, K, V) = V\cdot \textbf{softmax}(K^T Q)
O=Attention(Q,K,V)=V⋅softmax(KTQ)

如果你看过其他文章，你应该会看到真正的最终公式如下：

 Attention 
(
Q
,
K
,
V
)
=
softmax
⁡
(
Q
K
T
d
k
)
V
\text { Attention }(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V
 Attention (Q,K,V)=softmax(dk​​QKT​)V

其实我们的公式和这个公式只差了一个转置和
d
k
\sqrt{d_k}
dk​​ 。转置不比多说，就是表示方式不同。

原公式的$Q,K,V$以及输出$O$，对应我们公式的
Q
T
,
K
T
,
V
T
Q^T,K^T,V^T
QT,KT,VT和
O
T
O^T
OT

1.8.
d
k
d_k
dk​是什么，为什么要除以
d
k
\sqrt{d_k}
dk​​

首先，
d
k
d_k
dk​是Q和K矩阵的行维度，也就是上面的
Q
d
k
×
d
Q_{d_k\times d}
Qdk​×d​中的
d
k
d_k
dk​ 。而矩阵相乘会放大原有矩阵的标准差，放大的倍数约为
d
k
\sqrt{d_k}
dk​​，为了将标准差缩放回原来的大小，所以要除以
d
k
\sqrt{d_k}
dk​​。

例如，假设
Q
n
×
d
k
Q_{n \times d_k}
Qn×dk​​ 和
K
n
×
d
k
K_{n\times d_k}
Kn×dk​​ 的均值为0，标准差为1。则矩阵
Q
K
T
QK^T
QKT 的均值为0，标准差为
d
k
\sqrt{d_k}
dk​​，矩阵相乘使得其标准差放大了
d
k
\sqrt{d_k}
dk​​倍

矩阵的均值就是把所有的元素加起来除以元素数量，方差同理。

可以通过以下代码验证这个结论（数学不好，只能通过实验验证结论了，哭）：

Q = np.random.normal(size=(123, 456)) # 生成均值为0，标准差为1的 Q和K
K = np.random.normal(size=(123, 456))
print("Q.std=%s, K.std=%s, \nQ·K^T.std=%s, Q·K^T/√d.std=%s" 
      % (Q.std(), K.std(), 
         Q.dot(K.T).std(), Q.dot(K.T).std() / np.sqrt(456)))

Q.std=0.9977961671085275, K.std=1.0000574599289282,
Q·K^T.std=21.240017020263437, Q·K^T/√d.std=0.9946549289466212

通过输出可以看到，Q和K的标准差都为1，但是两矩阵相乘后，标准差却变为了 21.24, 通过除以
d
k
\sqrt{d_k}
dk​​，标准差又重新变为了 1

再看另一个例子，该例子Q和K的标准差是随机的，更符合真实的情况：

Q = np.random.normal(loc=1.56, scale=0.36, size=(123, 456)) # 生成均值为随机，标准差为随机的 Q和K
K = np.random.normal(loc=-0.34, scale=1.2, size=(123, 456))
print("Q.std=%s, K.std=%s, \nQ·K^T.std=%s, Q·K^T/√d.std=%s" 
      % (Q.std(), K.std(), 
         Q.dot(K.T).std(), Q.dot(K.T).std() / np.sqrt(456)))

Q.std=0.357460640868945, K.std=1.204536717914841,
Q·K^T.std=37.78368871510589, Q·K^T/√d.std=1.769383337989377

可以看到，最开始Q的标准差为 $0.35$, K的标准差为 $1.20$，结果矩阵相乘后标准差达到了 $37.78$， 经过缩放后，标准差又回到了$1.76$。

1.9. 代码实战：Pytorch定义SelfAttention模型

接下来使用Pytorch来定义SelfAttention模型，这里使用原论文中的公式：

 Attention 
(
Q
,
K
,
V
)
=
softmax
⁡
(
Q
K
T
d
k
)
V
\text { Attention }(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V
 Attention (Q,K,V)=softmax(dk​​QKT​)V

这里为了使代码定义逻辑更清晰，下面我将各个部分的维度标记出来：

O
n
×
d
v
=
 Attention 
(
Q
n
×
d
k
,
K
n
×
d
k
,
V
n
×
d
v
)
=
softmax
⁡
(
Q
n
×
d
k
K
d
k
×
n
T
d
k
)
V
n
×
d
v
=
A
n
×
n
′
V
n
×
d
v
\begin{aligned} O_{n\times d_v} = \text { Attention }(Q_{n\times d_k}, K_{n\times d_k}, V_{n\times d_v})&=\operatorname{softmax}\left(\frac{Q_{n\times d_k} K^{T}_{d_k\times n}}{\sqrt{d_k}}\right) V_{n\times d_v} \\\\ & = A'_{n\times n} V_{n\times d_v} \end{aligned}
On×dv​​= Attention (Qn×dk​​,Kn×dk​​,Vn×dv​​)​=softmax(dk​​Qn×dk​​Kdk​×nT​​)Vn×dv​​=An×n′​Vn×dv​​​

其中，各个变量定义为：

• $n$：input_num，输入向量的数量，例如，你一句话包含20个单词，则该值为20
• 
  d
  k
  d_k
  dk​：dimension of K，Q和K矩阵的行维度（超参数，需要自己调，一般和输入向量维度 $d$ 一致即可），该值决定了线性层的宽度。
• 
  d
  v
  d_v
  dv​：dimension of V，V矩阵的行维度，该值为输出向量的维度（超参数，需要自己调，一般取值和输入向量维度 $d$ 保持一致）。

上述公式中，$Q,K,V$是通过矩阵
W
q
,
W
k
,
W
v
W^q,W^k,W^v
Wq,Wk,Wv和输入向量 $I$ 计算出来的，而一般对于要训练的矩阵，代码中一般使用线性层来表示，详情可参考：Pytorch nn.Linear的基本用法，所以最终 $Q$ 矩阵的计算公式为：

Q
n
×
d
k
=
I
n
×
d
W
d
×
d
k
q
        
(
2
)
Q_{n \times d_k} = I_{n\times d} W^q_{d\times d_k} ~~~~~~~~(2)
Qn×dk​​=In×d​Wd×dk​q​        (2)

$K,V$ 矩阵同理。其中

• $d$：input_vector_dim: 输入向量的维度，例如你将单词编码为了10维的向量，则该值为10

有了公式(1)和(2)，就可以定义SelfAttention模型了，代码如下：

class SelfAttention(nn.Module):
    def __init__(self, input_vector_dim: int, dim_k=None, dim_v=None):
        """
        初始化SelfAttention，包含如下关键参数：
        input_vector_dim: 输入向量的维度，对应上述公式中的d，例如你将单词编码为了10维的向量，则该值为10
        dim_k: 矩阵W^k和W^q的维度
        dim_v: 输出向量的维度，即b的维度，例如，经过Attention后的输出向量b，如果你想让他的维度为15，则该值为15，若不填，则取input_vector_dim
        """
        super(SelfAttention, self).__init__()
        self.input_vector_dim = input_vector_dim
        # 如果 dim_k 和 dim_v 为 None，则取输入向量的维度
        if dim_k is None:
            dim_k = input_vector_dim
        if dim_v is None:
            dim_v = input_vector_dim
        """
        实际写代码时，常用线性层来表示需要训练的矩阵，方便反向传播和参数更新
        """
        self.W_q = nn.Linear(input_vector_dim, dim_k, bias=False)
        self.W_k = nn.Linear(input_vector_dim, dim_k, bias=False)
        self.W_v = nn.Linear(input_vector_dim, dim_v, bias=False)
        # 这个是根号下d_k
        self._norm_fact = 1 / np.sqrt(dim_k)
    def forward(self, x):
        """
        进行前向传播：
        x: 输入向量，size为(batch_size, input_num, input_vector_dim)
        """
        # 通过W_q, W_k, W_v矩阵计算出，Q,K,V
        # Q,K,V矩阵的size为 (batch_size, input_num, output_vector_dim)
        Q = self.W_q(x)
        K = self.W_k(x)
        V = self.W_v(x)
        # permute用于变换矩阵的size中对应元素的位置，
        # 即，将K的size由(batch_size, input_num, output_vector_dim)，变为(batch_size, output_vector_dim，input_num)
        # 0,1,2 代表各个元素的下标，即变换前，batch_size所在的位置是0，input_num所在的位置是1
        K_T = K.permute(0, 2, 1)
        # bmm是batch matrix-matrix product，即对一批矩阵进行矩阵相乘
        # bmm详情参见：https://pytorch.org/docs/stable/generated/torch.bmm.html
        atten = nn.Softmax(dim=-1)(torch.bmm(Q, K_T) * self._norm_fact）
        # 最后再乘以 V
        output = torch.bmm(atten, V)
        return output

接下来使用一下，定义50个为一批(batch_size=50)，输入向量维度为3， 一次输入5个向量，欲经过Attention层后，编码成5个4维的向量：

model = SelfAttention(3, 5, 4)
model(torch.Tensor(50,5,3)).size()

torch.Size([50, 5, 4])

Attention模型一般作为整体模型的一部分，是套在其他模型中使用的，最经典的莫过于Transformer

二. MultiHead Attention

2.1 MultiHead Attention理论讲解

在Transformer中使用的是MultiHead Attention，其实这玩意和Self Attention区别并不是很大。先明确以下几点，然后再开始讲解：

1. MultiHead的head不管有几个，参数量都是一样的。并不是head多，参数就多。
2. 当MultiHead的head为1时，并不等价于Self Attetnion，MultiHead Attention和Self Attention是不一样的东西
3. MultiHead Attention使用的也是Self Attention的公式
4. MultiHead除了
   W
   q
   ,
   W
   k
   ,
   W
   v
   W^q, W^k, W^v
   Wq,Wk,Wv三个矩阵外，还要多额外定义一个
   W
   o
   W^o
   Wo。

好了，知道上面几点，我们就可以开始讲解MultiHeadAttention了。

MultiHead Attention大部分逻辑和Self Attention是一致的，是从求出Q,K,V后开始改变的，所以我们就从这里开始讲解。

现在我们求出了Q, K, V矩阵，对于Self-Attention，我们已经可以带入公式了，用图像表示则为：

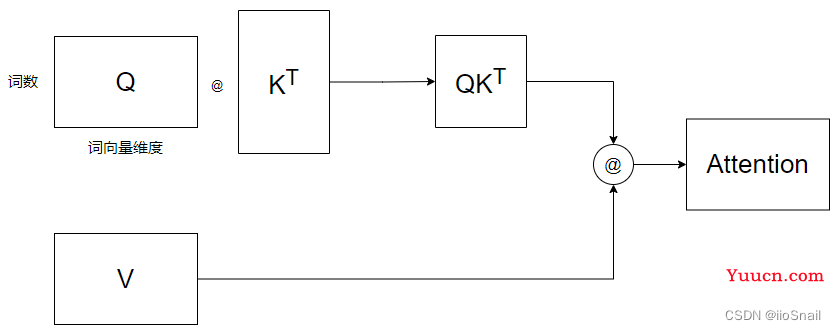
为了简单起见，该图忽略了Softmax和
d
k
d_k
dk​ 的计算

而MultiHead Attention在带入公式前做了一件事情，就是拆，它按照“词向量维度”这个方向，将Q,K,V拆成了多个头，如图所示：

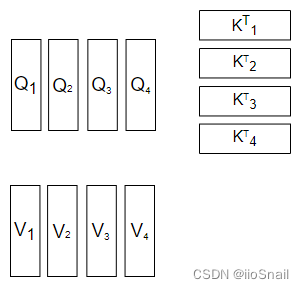
这里我的head数为4。既然拆成了多个head，那么之后的计算，也是各自的head进行计算，如图所示：

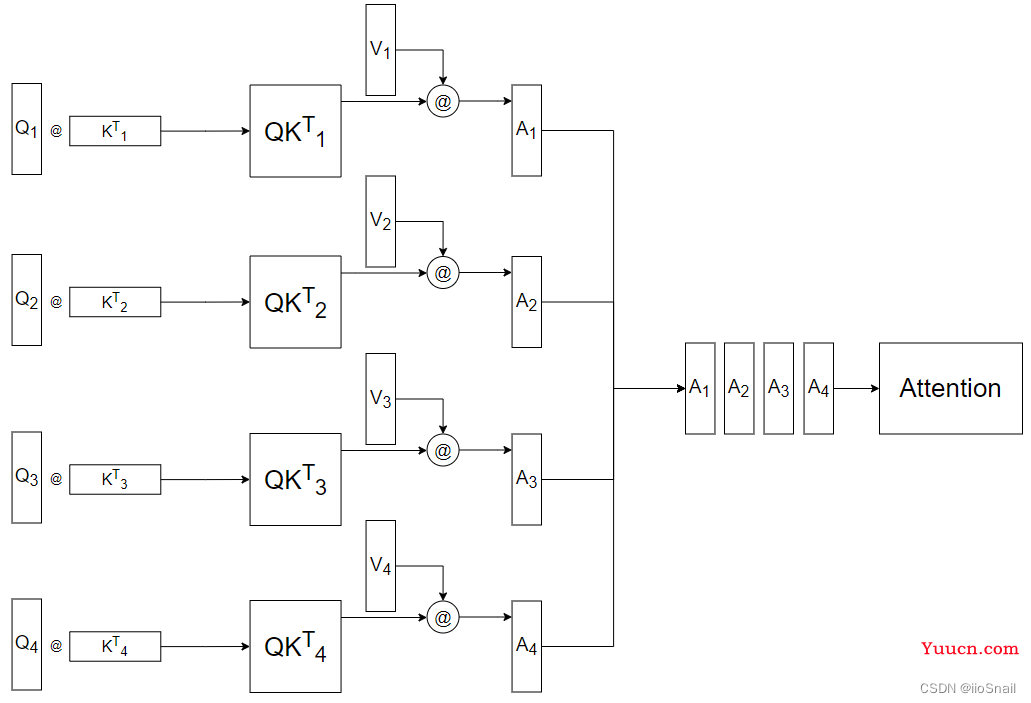
但这样拆开来计算的Attention使用Concat进行合并效果并不太好，所以最后需要再采用一个额外的
W
o
W^o
Wo矩阵，对Attention再进行一次线性变换，如图所示：

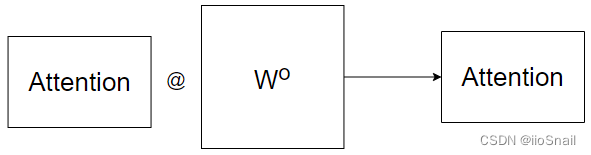
到这里也能看出来，head数并不是越多越好。而为什么要用MultiHead Attention，Transformer给出的解释为：Multi-head attention允许模型共同关注来自不同位置的不同表示子空间的信息。反正就是用了比不用好。

2.2. Pytorch实现MultiHead Attention

该代码参考项目annotated-transformer。

首先定义一个通用的Attention函数：

def attention(query, key, value):
    """
    计算Attention的结果。
    这里其实传入的是Q,K,V，而Q,K,V的计算是放在模型中的，请参考后续的MultiHeadedAttention类。
    这里的Q,K,V有两种Shape，如果是Self-Attention，Shape为(batch, 词数, d_model)，
                           例如(1, 7, 128)，即batch_size为1，一句7个单词，每个单词128维
                           但如果是Multi-Head Attention，则Shape为(batch, head数, 词数，d_model/head数)，
                           例如(1, 8, 7, 16)，即Batch_size为1，8个head，一句7个单词，128/8=16。
                           这样其实也能看出来，所谓的MultiHead其实就是将128拆开了。
                           在Transformer中，由于使用的是MultiHead Attention，所以Q,K,V的Shape只会是第二种。
    """
    # 获取d_model的值。之所以这样可以获取，是因为query和输入的shape相同，
    # 若为Self-Attention，则最后一维都是词向量的维度，也就是d_model的值。
    # 若为MultiHead Attention，则最后一维是 d_model / h，h为head数
    d_k = query.size(-1)
    # 执行QK^T / √d_k
    scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)
    # 执行公式中的Softmax
    # 这里的p_attn是一个方阵
    # 若是Self Attention，则shape为(batch, 词数, 次数)，例如(1, 7, 7)
    # 若是MultiHead Attention，则shape为(batch, head数, 词数，词数)
    p_attn = scores.softmax(dim=-1)
    # 最后再乘以 V。
    # 对于Self Attention来说，结果Shape为(batch, 词数, d_model)，这也就是最终的结果了。
    # 但对于MultiHead Attention来说，结果Shape为(batch, head数, 词数，d_model/head数)
    # 而这不是最终结果，后续还要将head合并，变为(batch, 词数, d_model)。不过这是MultiHeadAttention
    # 该做的事情。
    return torch.matmul(p_attn, value)
class MultiHeadedAttention(nn.Module):
    def __init__(self, h, d_model):
        """
        h: head的数量
        """
        super(MultiHeadedAttention, self).__init__()
        assert d_model % h == 0
        # We assume d_v always equals d_k
        self.d_k = d_model // h
        self.h = h
        # 定义W^q, W^k, W^v和W^o矩阵。
        # 如果你不知道为什么用nn.Linear定义矩阵，可以参考该文章：
        # https://blog.csdn.net/zhaohongfei_358/article/details/122797190
        self.linears = [
            nn.Linear(d_model, d_model),
            nn.Linear(d_model, d_model),
            nn.Linear(d_model, d_model),
            nn.Linear(d_model, d_model),
        ]
    def forward(self, x):
        # 获取Batch Size
        nbatches = x.size(0)
        """
        1. 求出Q, K, V，这里是求MultiHead的Q,K,V，所以Shape为(batch, head数, 词数，d_model/head数)
            1.1 首先，通过定义的W^q,W^k,W^v求出SelfAttention的Q,K,V，此时Q,K,V的Shape为(batch, 词数, d_model)
                对应代码为 `linear(x)`
            1.2 分成多头，即将Shape由(batch, 词数, d_model)变为(batch, 词数, head数，d_model/head数)。
                对应代码为 `view(nbatches, -1, self.h, self.d_k)`
            1.3 最终交换“词数”和“head数”这两个维度，将head数放在前面，最终shape变为(batch, head数, 词数，d_model/head数)。
                对应代码为 `transpose(1, 2)`
        """
        query, key, value = [
            linear(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
            for linear, x in zip(self.linears, (x, x, x))
        ]
        """
        2. 求出Q,K,V后，通过attention函数计算出Attention结果，
           这里x的shape为(batch, head数, 词数，d_model/head数)
           self.attn的shape为(batch, head数, 词数，词数)
        """
        x = attention(
            query, key, value
        )
        """
        3. 将多个head再合并起来，即将x的shape由(batch, head数, 词数，d_model/head数)
           再变为 (batch, 词数，d_model)
           3.1 首先，交换“head数”和“词数”，这两个维度，结果为(batch, 词数, head数, d_model/head数)
               对应代码为：`x.transpose(1, 2).contiguous()`
           3.2 然后将“head数”和“d_model/head数”这两个维度合并，结果为(batch, 词数，d_model)
        """
        x = (
            x.transpose(1, 2)
                .contiguous()
                .view(nbatches, -1, self.h * self.d_k)
        )
        # 最终通过W^o矩阵再执行一次线性变换，得到最终结果。
        return self.linears[-1](x)

接下来尝试使用一下：

# 定义8个head，词向量维度为512
model = MultiHeadedAttention(8, 512)
# 传入一个batch_size为2， 7个单词，每个单词为512维度
x = torch.rand(2, 7, 512)
# 输出Attention后的结果
print(model(x).size())

输出为：

torch.Size([2, 7, 512])

三. Masked Attention

3.1 为什么要使用Mask掩码

在Transformer中的Decoder中有一个Masked MultiHead Attention。本节来对其进行一个详细的讲解。

首先我们来复习一下Attention的公式：

O
n
×
d
v
=
 Attention 
(
Q
n
×
d
k
,
K
n
×
d
k
,
V
n
×
d
v
)
=
softmax
⁡
(
Q
n
×
d
k
K
d
k
×
n
T
d
k
)
V
n
×
d
v
=
A
n
×
n
′
V
n
×
d
v
\begin{aligned} O_{n\times d_v} = \text { Attention }(Q_{n\times d_k}, K_{n\times d_k}, V_{n\times d_v})&=\operatorname{softmax}\left(\frac{Q_{n\times d_k} K^{T}_{d_k\times n}}{\sqrt{d_k}}\right) V_{n\times d_v} \\\\ & = A'_{n\times n} V_{n\times d_v} \end{aligned}
On×dv​​= Attention (Qn×dk​​,Kn×dk​​,Vn×dv​​)​=softmax(dk​​Qn×dk​​Kdk​×nT​​)Vn×dv​​=An×n′​Vn×dv​​​

其中：

O
n
×
d
v
=
[
o
1
o
2
⋮
o
n
]
,
    
A
n
×
n
′
=
[
α
1
,
1
′
α
2
,
1
′
⋯
α
n
,
1
′
α
1
,
2
′
α
2
,
2
′
⋯
α
n
,
2
′
⋮
⋮
⋮
α
1
,
n
′
α
2
,
n
′
⋯
α
n
,
n
′
]
,
    
V
n
×
d
v
=
[
v
1
v
2
⋮
v
n
]
O_{n\times d_v}= \begin{bmatrix} o_1\\ o_2\\ \vdots \\ o_n\\ \end{bmatrix},~~~~A'_{n\times n} = \begin{bmatrix} \alpha'_{1,1} & \alpha'_{2,1} & \cdots &\alpha'_{n,1} \\ \alpha'_{1,2} & \alpha'_{2,2} & \cdots &\alpha'_{n,2} \\ \vdots & \vdots & &\vdots \\ \alpha'_{1,n} & \alpha'_{2,n} & \cdots &\alpha'_{n,n} \\ \end{bmatrix}, ~~~~V_{n\times d_v}= \begin{bmatrix} v_1\\ v_2\\ \vdots \\ v_n\\ \end{bmatrix}
On×dv​​=​o1​o2​⋮on​​​,    An×n′​=​α1,1′​α1,2′​⋮α1,n′​​α2,1′​α2,2′​⋮α2,n′​​⋯⋯⋯​αn,1′​αn,2′​⋮αn,n′​​​,    Vn×dv​​=​v1​v2​⋮vn​​​

假设
(
v
1
,
v
2
,
.
.
.
v
n
)
(v_1, v_2, ... v_n)
(v1​,v2​,...vn​) 对应着 $(机,器,学,习,真,好,玩)$。那么
(
o
1
,
o
2
,
.
.
.
,
o
n
)
(o_1, o_2, ..., o_n)
(o1​,o2​,...,on​) 就对应着
(
机
′
,
器
′
,
学
′
,
习
′
,
真
′
,
好
′
,
玩
′
)
(机', 器', 学', 习', 真', 好', 玩')
(机′,器′,学′,习′,真′,好′,玩′)。 其中
机
′
机'
机′ 包含着
v
1
v_1
v1​ 到
v
n
v_n
vn​ 的所有注意力信息。而计算
机
′
机'
机′ 时的 $(机,器,...)$ 这些字的权重就是
A
′
A'
A′ 的第一行的
(
α
1
,
1
′
,
α
2
,
1
′
,
.
.
.
)
(\alpha'_{1,1}, \alpha'_{2,1}, ...)
(α1,1′​,α2,1′​,...)。

如果上面的回忆起来了，那么接下来看一下Transformer的用法，假设我们是要用Transformer翻译“Machine learning is fun”这句话。

首先，我们会将“Machine learning is fun” 送给Encoder，输出一个名叫Memory的Tensor，如图所示：

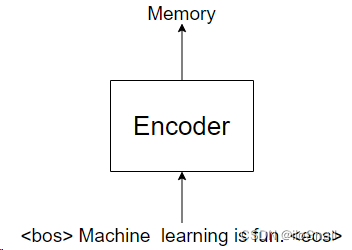
之后我们会将该Memory作为Decoder的一个输入，使用Decoder预测。Decoder并不是一下子就能把“机器学习真好玩”说出来，而是一个词一个词说（或一个字一个字，这取决于你的分词方式），如图所示：

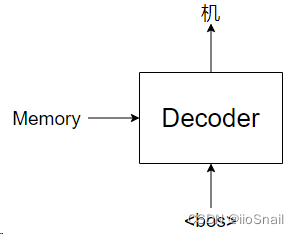
紧接着，我们会再次调用Decoder，这次是传入“<bos> 机”：

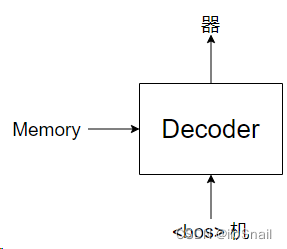
依次类推，直到最后输出<eos>结束：

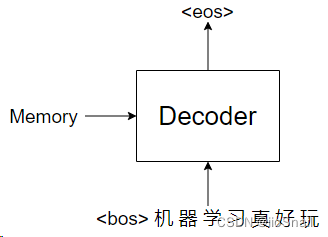
当Transformer输出<eos>时，预测就结束了。

到这里我们就会发现，对于Decoder来说是一个字一个字预测的，所以假设我们Decoder的输入是“机器学习”时，“习”字只能看到前面的“机器学”三个字，所以此时对于“习”字只有“机器学习”四个字的注意力信息。

但是，例如最后一步传的是“<bos>机器学习真好玩”，还是不能让“习”字看到后面“真好玩”三个字，所以要使用mask将其盖住，这又是为什么呢？原因是：如果让“习”看到了后面的字，那么“习”字的编码就会发生变化。

我们不妨来分析一下：

一开始我们只传入了“机”（忽略bos），此时使用attention机制，将“机”字编码为了 $[0.13,0.73,...]$

第二次，我们传入了“机器”，此时使用attention机制，如果我们不将“器”字盖住的话，那“机”字的编码就会发生变化，它就不再是是$[0.13,0.73,...]$了，也许就变成了$[0.95,0.81,...]$。

这就会导致第一次“机”字的编码是$[0.13,0.73,...]$，第二次却变成了$[0.95,0.81,...]$，这样就可能会让网络有问题。所以我们为了不让“机”字的编码产生变化，所以我们要使用mask，掩盖住“机”字后面的字，也就是即使他能attention后面的字，也不让他attention。

3.2 如何进行mask掩码

要进行掩码，只需要对scores动手就行了，也就是
A
n
×
n
′
A'_{n\times n}
An×n′​ 。直接上例子：

第一次，我们只有
v
1
v_1
v1​ 变量，所以是：

[
o
1
]
=
[
α
1
,
1
′
]
⋅
[
v
1
]
\begin{bmatrix} o_1\\ \end{bmatrix}=\begin{bmatrix} \alpha'_{1,1} \end{bmatrix} \cdot \begin{bmatrix} v_1\\ \end{bmatrix}
[o1​​]=[α1,1′​​]⋅[v1​​]

第二次，我们有
v
1
,
v
2
v_1, v_2
v1​,v2​ 两个变量：

[
o
1
o
2
]
=
[
α
1
,
1
′
α
2
,
1
′
α
1
,
2
′
α
2
,
2
′
]
[
v
1
v
2
]
\begin{bmatrix} o_1\\ o_2 \end{bmatrix} = \begin{bmatrix} \alpha'_{1,1} & \alpha'_{2,1} \\ \alpha'_{1,2} & \alpha'_{2,2} \end{bmatrix} \begin{bmatrix} v_1\\ v_2\\ \end{bmatrix}
[o1​o2​​]=[α1,1′​α1,2′​​α2,1′​α2,2′​​][v1​v2​​]

此时如果我们不对
A
2
×
2
′
A'_{2\times 2}
A2×2′​ 进行掩码的话，
o
1
o_1
o1​的值就会发生变化（第一次是
α
1
,
1
′
v
1
\alpha'_{1,1}v_1
α1,1′​v1​，第二次却变成了
α
1
,
1
′
v
1
+
α
2
,
1
′
v
2
\alpha'_{1,1}v_1+\alpha'_{2,1}v_2
α1,1′​v1​+α2,1′​v2​）。那这样看，我们只需要将
α
2
,
1
′
\alpha'_{2,1}
α2,1′​ 盖住即可，这样就能保证两次的
o
1
o_1
o1​ 一致了。

所以第二次实际就为：

[
o
1
o
2
]
=
[
α
1
,
1
′
α
1
,
2
′
α
2
,
2
′
]
[
v
1
v
2
]
\begin{bmatrix} o_1\\ o_2 \end{bmatrix} = \begin{bmatrix} \alpha'_{1,1} & 0 \\ \alpha'_{1,2} & \alpha'_{2,2} \end{bmatrix} \begin{bmatrix} v_1\\ v_2\\ \end{bmatrix}
[o1​o2​​]=[α1,1′​α1,2′​​0α2,2′​​][v1​v2​​]

依次类推，如果我们执行到第$n$次时，就应该变成：

[
o
1
o
2
⋮
o
n
]
=
[
α
1
,
1
′
⋯
α
1
,
2
′
α
2
,
2
′
⋯
⋮
⋮
⋮
α
1
,
n
′
α
2
,
n
′
⋯
α
n
,
n
′
]
[
v
1
v
2
⋮
v
n
]
\begin{bmatrix} o_1\\ o_2\\ \vdots \\ o_n\\ \end{bmatrix} = \begin{bmatrix} \alpha'_{1,1} & 0 & \cdots & 0 \\ \alpha'_{1,2} & \alpha'_{2,2} & \cdots & 0 \\ \vdots & \vdots & &\vdots \\ \alpha'_{1,n} & \alpha'_{2,n} & \cdots &\alpha'_{n,n} \\ \end{bmatrix} \begin{bmatrix} v_1\\ v_2\\ \vdots \\ v_n\\ \end{bmatrix}
​o1​o2​⋮on​​​=​α1,1′​α1,2′​⋮α1,n′​​0α2,2′​⋮α2,n′​​⋯⋯⋯​00⋮αn,n′​​​​v1​v2​⋮vn​​​

3.3 为什么是负无穷而不是0

按照上面的说法，mask掩码是0，但为什么源码中的掩码是 $-1e9$ （负无穷）。Attention部分源码如下：

if mask is not None:
    scores = scores.masked_fill(mask == 0, -1e9)
p_attn = scores.softmax(dim=-1)

你仔细看，我们上面说的
A
n
×
n
′
A'_{n\times n}
An×n′​ 是什么，是softmax之后的。而源码中呢， 源码是在softmax之前进行掩码，所以才是负无穷，因为将负无穷softmax后就会变成0了。

3.4. 训练时的掩码

通常我们在网上看Masked Attention相关的文章时，会说mask的目的是为了防止网络看到不该看到的内容。本节主要来解释一下这句话。

首先，我们需要了解一下Transformer的训练过程。

在Transformer推理时，我们是一个词一个词的输出，但在训练时这样做效率太低了，所以我们会将target一次性给到Transformer（当然，你也可以按照推理过程做），如图所示：

从图上可以看出，Transformer的训练过程和推理过程主要有以下几点异同：

1. 源输入src相同：对于Transformer的inputs部分(src参数)一样，都是要被翻译的句子。
2. 目标输入tgt不同：在Transformer推理时，tgt是从<bos>开始，然后每次加入上一次的输出（第二次输入为<bos> 我）。但在训练时是一次将“完整”的结果给到Transformer，这样其实和一个一个给结果上一致。这里还有一个细节，就是tgt比src少了一位，src是7个token，而tgt是6个token。这是因为我们在最后一次推理时，只会传入前n-1个token。举个例子：假设我们要预测<bos> 我 爱 你 <eos>（这里忽略pad），我们最后一次的输入tgt是<bos> 我 爱 你（没有<eos>），因此我们的输入tgt一定不会出现目标的最后一个token，所以一般tgt处理时会将目标句子删掉最后一个token。
3. 输出数量变多：在训练时，transformer会一次输出多个概率分布。例如上图，我就的等价于是tgt为<bos>时的输出，爱就等价于tgt为<bos> 我时的输出，依次类推。当然在训练时，得到输出概率分布后就可以计算loss了，并不需要将概率分布再转成对应的文字。注意这里也有个细节，我们的输出数量是6，对应到token就是我 爱 你 <eos> <pad> <pad>，这里少的是<bos>，因为<bos>不需要预测。计算loss时，我们也是要和的这几个token进行计算，所以我们的label不包含<bos>。代码中通常命名为tgt_y。

其实总结一下就一句话：Transformer推理时是一个一个词预测，而训练时会把所有的结果一次性给到Transformer，但效果等同于一个一个词给，而之所以可以达到该效果，就是因为对tgt进行了掩码，防止其看到后面的信息，也就是不要让前面的字具备后面字的上下文信息。

可能看了这句总结还是很难理解，所以我们接下来来做个实验，我们的实验内容为：首先模拟Transformer的推理过程，然后再模拟Transformer的训练过程，看看训练时一次性给到所有的tgt和推理时一个一个给的结果是否一致。

这里我们要用到Pytorch中的nn.Transformer，用法可参考这篇文章。

首先我们来定义模型：

# 词典数为10， 词向量维度为8
embedding = nn.Embedding(10, 8)
# 定义Transformer，注意一定要改成eval模型，否则每次输出结果不一样
transformer = nn.Transformer(d_model=8, batch_first=True).eval()

接下来定义我们的src和tgt：

# Encoder的输入
src = torch.LongTensor([[0, 1, 2, 3, 4]])
# Decoder的输入
tgt = torch.LongTensor([[4, 3, 2, 1, 0]])

然后我们将[4]送给Transformer进行预测，模拟推理时的第一步：

transformer(embedding(src), embedding(tgt[:, :1]),
            # 这个就是用来生成阶梯式的mask的
            tgt_mask=nn.Transformer.generate_square_subsequent_mask(1))

tensor([[[ 1.4053, -0.4680,  0.8110,  0.1218,  0.9668, -1.4539, -1.4427,
           0.0598]]], grad_fn=<NativeLayerNormBackward0>)

然后我们将[4, 3]送给Transformer，模拟推理时的第二步：

transformer(embedding(src), embedding(tgt[:, :2]), tgt_mask=nn.Transformer.generate_square_subsequent_mask(2))

tensor([[[ 1.4053, -0.4680,  0.8110,  0.1218,  0.9668, -1.4539, -1.4427,
           0.0598],
         [ 1.2726, -0.3516,  0.6584,  0.3297,  1.1161, -1.4204, -1.5652,
          -0.0396]]], grad_fn=<NativeLayerNormBackward0>)

这个时候你有没有发现，输出的第一个向量和上面那个一模一样。

最后我们再将tgt一次性送给transformer，模拟训练过程：

transformer(embedding(src), embedding(tgt), tgt_mask=nn.Transformer.generate_square_subsequent_mask(5))

tensor([[[ 1.4053, -0.4680,  0.8110,  0.1218,  0.9668, -1.4539, -1.4427,
           0.0598],
         [ 1.2726, -0.3516,  0.6584,  0.3297,  1.1161, -1.4204, -1.5652,
          -0.0396],
         [ 1.4799, -0.3575,  0.8310,  0.1642,  0.8811, -1.3140, -1.5643,
          -0.1204],
         [ 1.4359, -0.6524,  0.8377,  0.1742,  1.0521, -1.3222, -1.3799,
          -0.1454],
         [ 1.3465, -0.3771,  0.9107,  0.1636,  0.8627, -1.5061, -1.4732,
           0.0729]]], grad_fn=<NativeLayerNormBackward0>)

看到没，前两个tensor和模拟推理时的输出结果一模一样。所以使用mask时，我们可以保证前面的词不会具备后面词的信息，这样就可以保证Transformer的输出不会因为传入词的多少而改变，从而我们就可以做到在训练时一次将tgt全部给到Transformer，却不会出现问题。这也就是人们常说的，防止网络训练时看到不该看到的内容。

可以尝试思考下为什么输出不会变，原因其实就是因为神经网络的本质就是不断的进行矩阵相乘，例如：
X
W
1
W
2
W
3
⋯
W
n
→
O
XW_1W_2W_3\cdots W_n \rightarrow O
XW1​W2​W3​⋯Wn​→O，$X$ 为输入， $O$ 为输出。在这之中，$X$ 的第二个行向量本身就不会让你的第一个行向量的结果改变。在Transformer中多个行向量会互相影响是因为Attention机制，因为里面存在有$X$自身的运算，类似于 $X\cdot X$，但我们通过mask可以保证 $X\cdot Mask\_X$ 的第二个行向量不要影响到第一个行向量。这里就不展开讲解了，可以尝试用纸笔算一下。

完结，如果有什么地方有错误，欢迎大家指出来。

参考资料

李宏毅Self-Attention: https://www.youtube.com/watch?v=hYdO9CscNes

超详细图解Self-Attention: https://zhuanlan.zhihu.com/p/410776234

Pytorch nn.Linear的基本用法：https://blog.csdn.net/zhaohongfei_358/article/details/122797190

极简翻译模型Demo，彻底理解Transformer：https://zhuanlan.zhihu.com/p/360343417

annotated-transformer：https://github.com/harvardnlp/annotated-transformer/