注意力机制-CA注意力-Coordinate attention

简介

CA（Coordinate attention for efficient mobile network design）发表在CVPR2021，帮助轻量级网络涨点、即插即用。

CA注意力机制的优势：

1、不仅考虑了通道信息，还考虑了方向相关的位置信息。
2、足够的灵活和轻量，能够简单的插入到轻量级网络的核心模块中。

提出不足

1、SE注意力中只关注构建通道之间的相互依赖关系，忽略了空间特征。
2、CBAM中引入了大尺度的卷积核提取空间特征，但忽略了长程依赖问题。

算法流程图

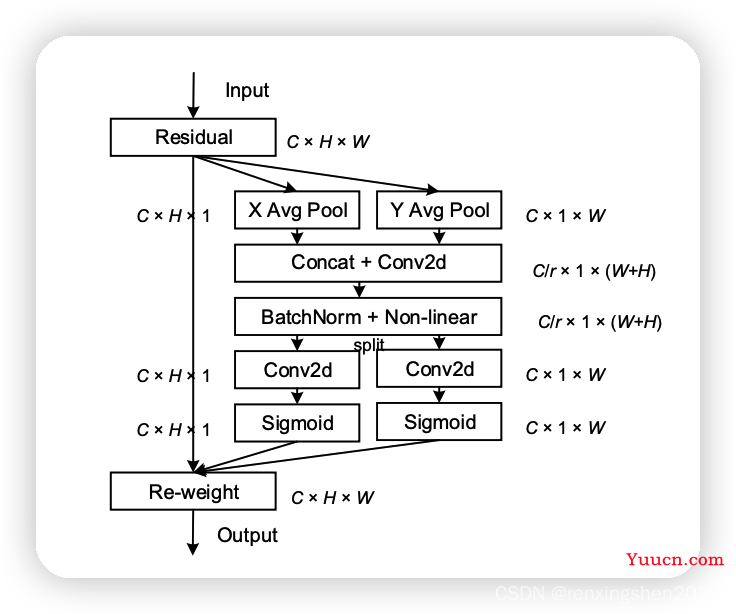
step1: 为了避免空间信息全部压缩到通道中，这里没有使用全局平均池化。为了能够捕获具有精准位置信息的远程空间交互，对全局平均池化进行的分解，具体如下：


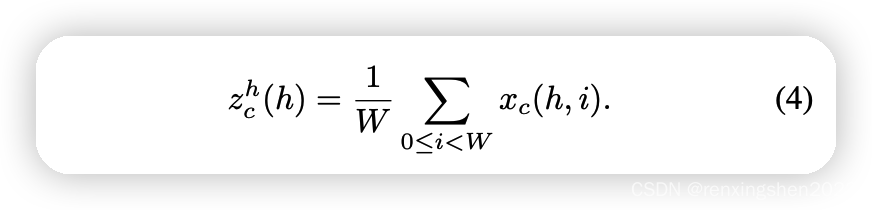
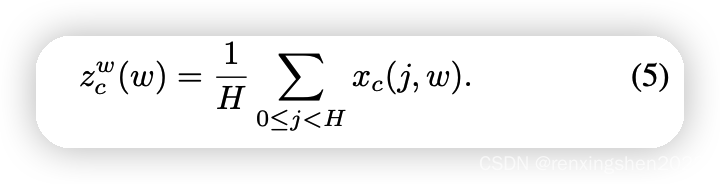
对尺寸为$C\ast H\ast W$输入特征图$Input$分别按照$X$方向和$Y$方向进行池化，分别生成尺寸为$C\ast H\ast 1$和$C\ast 1\ast W$的特征图。如下图所示（图片粘贴自B站大佬渣渣的熊猫潘）。

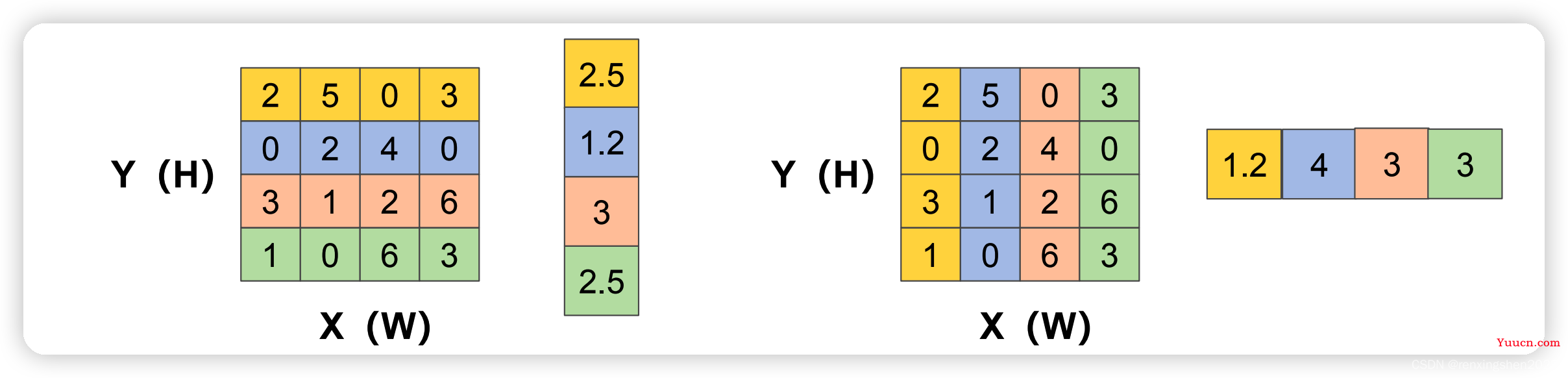
step2:将生成的$C\ast 1\ast W$的特征图进行变换，然后进行concat操作。公式如下：

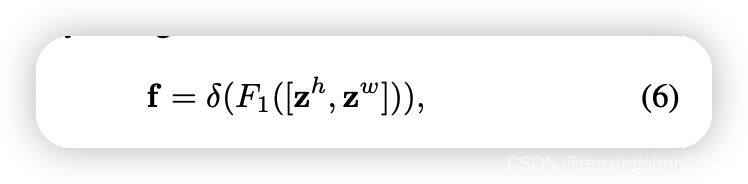
将
z
h
z^h
zh和
z
w
z^w
zw进行concat后生成如下图所示的特征图，然后进行F1操作（利用1*1卷积核进行降维，如SE注意力中操作）和激活操作，生成特征图
f
∈
R
C
/
r
×
(
H
+
W
)
×
1
f \in \mathbb{R}^{C/r\times(H+W)\times1}
f∈RC/r×(H+W)×1。

step3:沿着空间维度，再将$f$进行split操作，分成
f
h
∈
R
C
/
r
×
H
×
1
f^h\in \mathbb{R}^{C/r\times H \times1}
fh∈RC/r×H×1和
f
w
∈
R
C
/
r
×
1
×
W
f^w\in \mathbb{R}^{C/r\times1\times W}
fw∈RC/r×1×W，然后分别利用$1\times 1$卷积进行升维度操作，再结合sigmoid激活函数得到最后的注意力向量
g
h
∈
R
C
×
H
×
1
g^h \in \mathbb{R}^{C \times H \times 1 }
gh∈RC×H×1和
g
w
∈
R
C
×
1
×
W
g^w\in \mathbb{R}^{C \times1\times W}
gw∈RC×1×W。

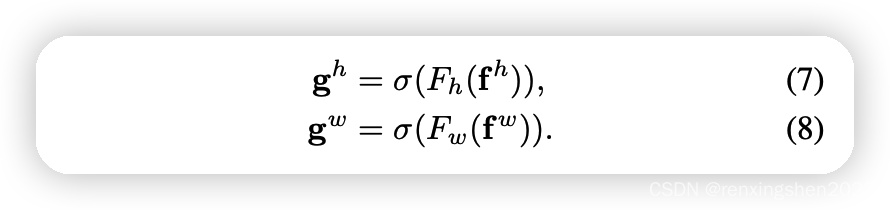
最后：Coordinate Attention 的输出公式可以写成：

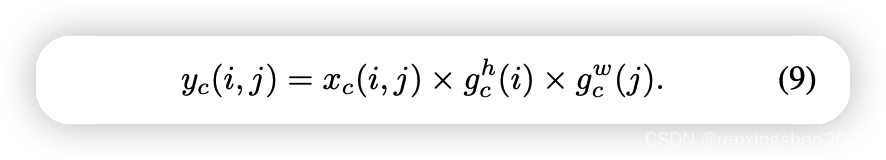
代码

代码粘贴自github。CoordAttention
地址：https://github.com/houqb/CoordAttention/blob/main/mbv2_ca.py

class CoordAtt(nn.Module):
    def __init__(self, inp, oup, groups=32):
        super(CoordAtt, self).__init__()
        self.pool_h = nn.AdaptiveAvgPool2d((None, 1))
        self.pool_w = nn.AdaptiveAvgPool2d((1, None))
        mip = max(8, inp // groups)
        self.conv1 = nn.Conv2d(inp, mip, kernel_size=1, stride=1, padding=0)
        self.bn1 = nn.BatchNorm2d(mip)
        self.conv2 = nn.Conv2d(mip, oup, kernel_size=1, stride=1, padding=0)
        self.conv3 = nn.Conv2d(mip, oup, kernel_size=1, stride=1, padding=0)
        self.relu = h_swish()
    def forward(self, x):
        identity = x
        n,c,h,w = x.size()
        x_h = self.pool_h(x)
        x_w = self.pool_w(x).permute(0, 1, 3, 2)
        y = torch.cat([x_h, x_w], dim=2)
        y = self.conv1(y)
        y = self.bn1(y)
        y = self.relu(y) 
        x_h, x_w = torch.split(y, [h, w], dim=2)
        x_w = x_w.permute(0, 1, 3, 2)
        x_h = self.conv2(x_h).sigmoid()
        x_w = self.conv3(x_w).sigmoid()
        x_h = x_h.expand(-1, -1, h, w)
        x_w = x_w.expand(-1, -1, h, w)
        y = identity * x_w * x_h
        return y

最后

CA不仅考虑到空间和通道之间的关系，还考虑到长程依赖问题。通过实验发现，CA不仅可以实现精度提升，且参数量、计算量较少。

简单进行记录，如有问题请大家指正。