发布时间：2023-03-31 文章分类：电脑基础投稿人：樱花字号：默认 | 大 | 超大打印

文章目录

Matlab 初步进行机器学习
- 实时脚本的介绍
- 导入数据
- 用导出模型进行预测
- 导出代码进行预测
- 决策树预测和可视化
- 交叉验证的测试集和随机数种子
计算F1分数和AUC，绘制ROC曲线
- 多分类问题F1分数计算
- Matlab计算F1分数
- ROC曲线与AUC曲线
网格搜索调参
- 关于调参
- - 调参的定义
  - 调参的目的
  - Matlab机器学习可以调的参数
  - 调参的方法
  - - 网格搜索
    - 随机搜索
    - 贝叶斯调参
- 网格搜索调参演示
阶段性总结：模型选择的一般步骤

Matlab 初步进行机器学习

实时脚本的介绍

类似一个笔记本，像是jupyter notebook

快捷键：

快速切换文本和代码格式：
- win:ctrl+e
- Mac:command+ctrl+e
可以运行当前节的代码
- win： Ctrl+Enter
- mac：command+enter
分节
- win：shift（？或者alt，我不清楚）+ctrl+enter
- mac：option+command+enter

视图中打开数据提示，将鼠标放在变量上，会显示变量的值，非常方便。

实时编辑器中要用到的函数，还是建议自己另外写一个.m文件，然后调用

导入数据

调整本地的数据的形式为标准形式

训练的数据放一个表，要预测的数据放一个表。

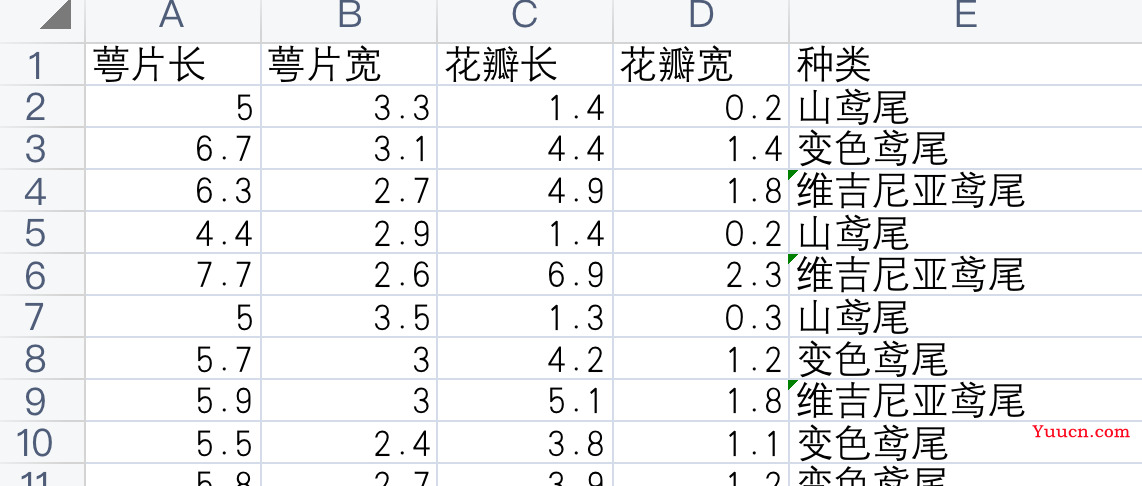
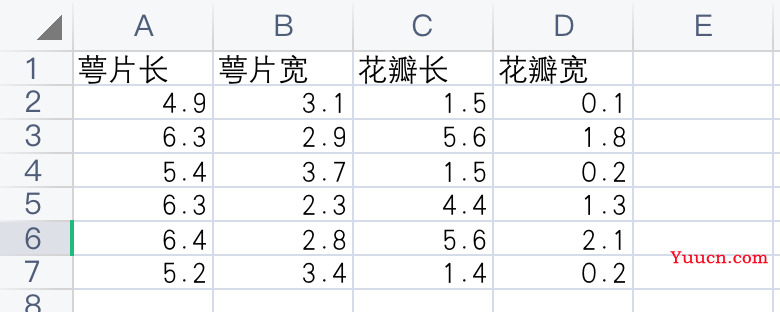
把不相关的指标都删掉（比如编号），因变量放最右边

在 matlab 中切换路径为当前文件夹，导入数据（格式为表，给指标（列名）改成英文导入的）

要保证两个表（一训练一预测）的指标名字要一样！

同时生成脚本，将脚本里内容复制到实时脚本mlx里，

用导出模型进行预测

导入完数据后，就可以使用分类学习器了，可以在上方的App中点击分类学习器（机器学习栏目中），也可以使用下面的代码调用。

classificationLearner
% 调用回归学习器的命令是regressionLearner

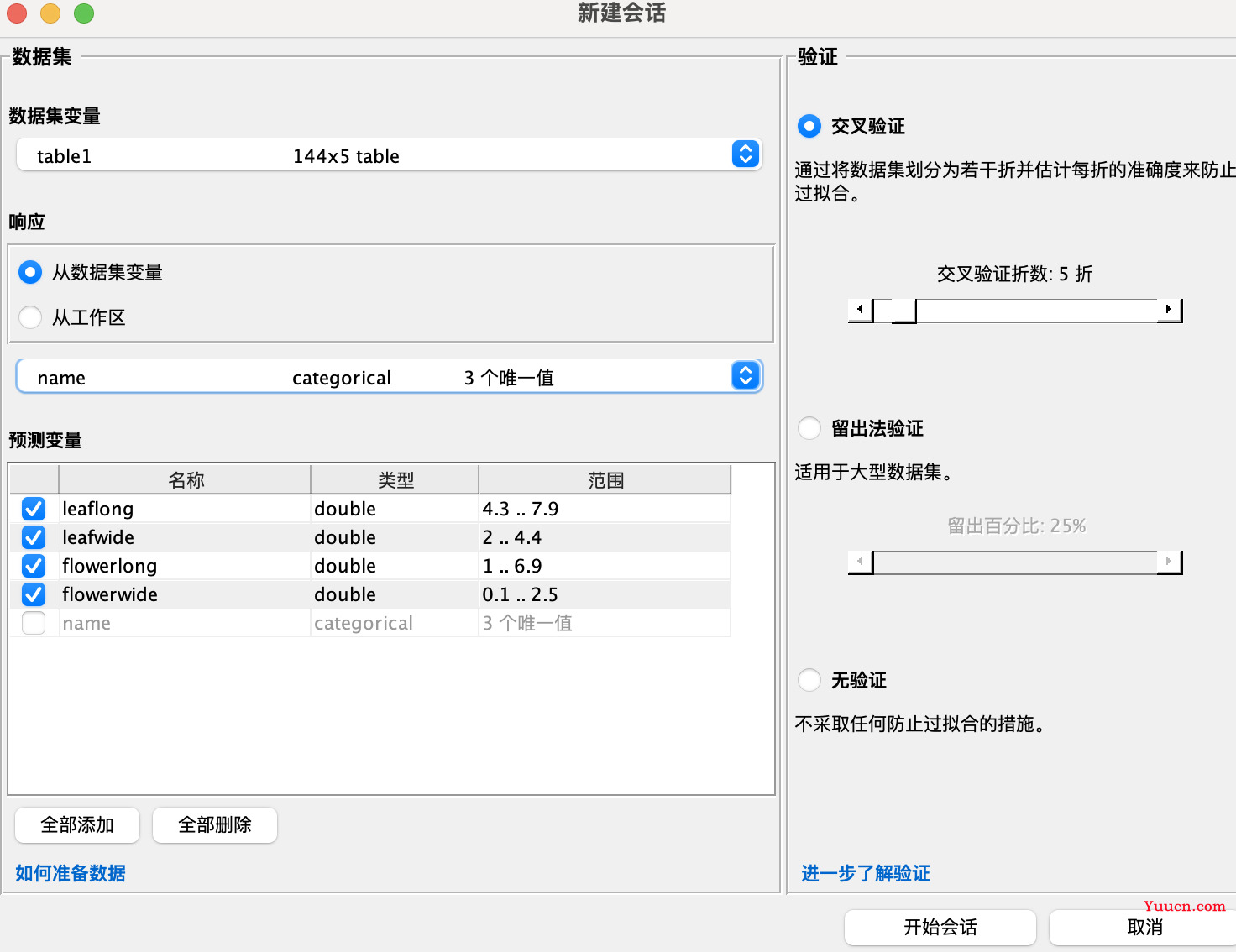
中间一条是要预测的变量
其他是自变量
如果不要也可以不勾选
验证
- 交叉验证
- 留出法验证
- 无验证
- 三者选一个

（3）选择模型进行训练，比较不同模型的好坏

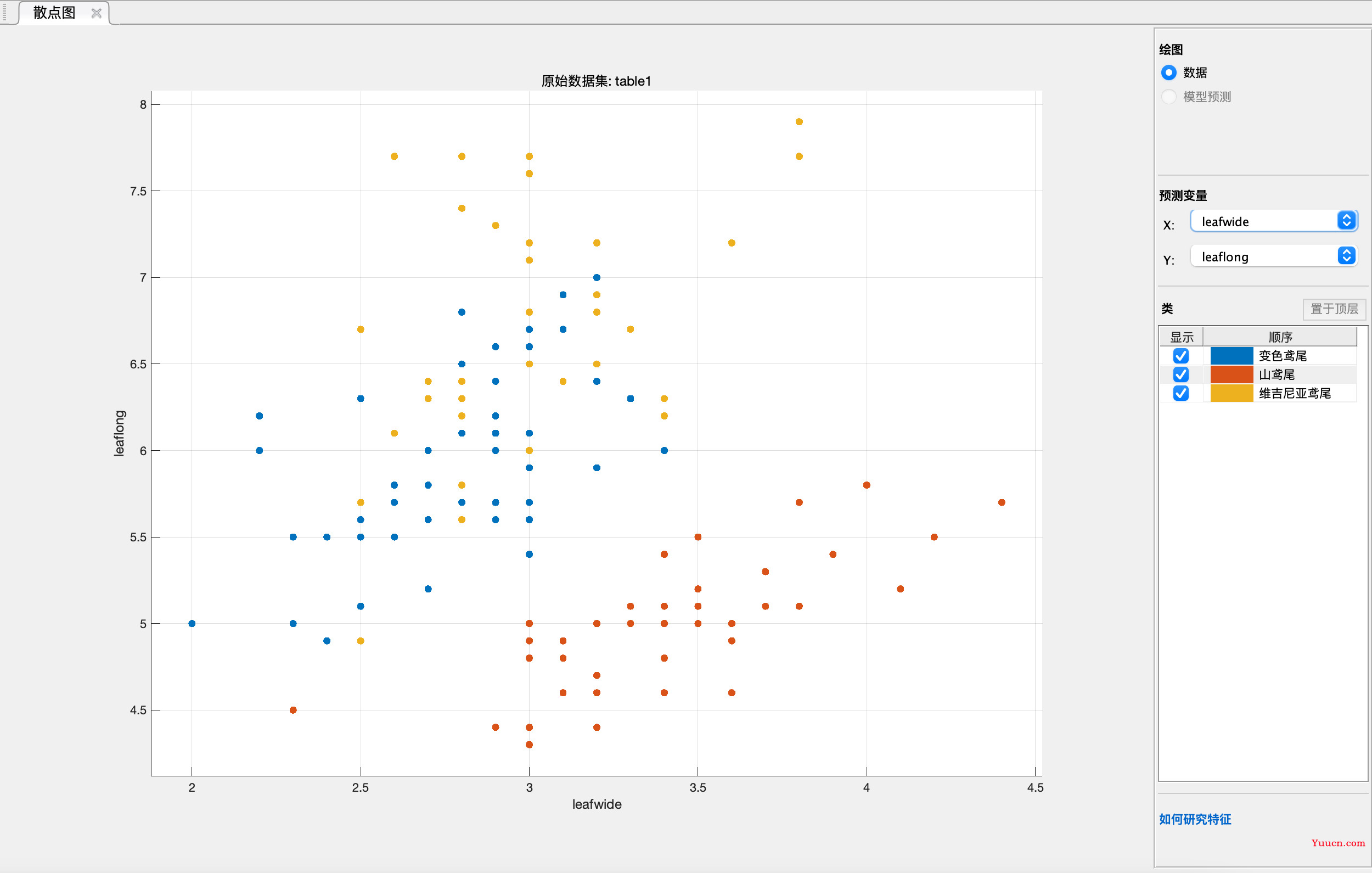
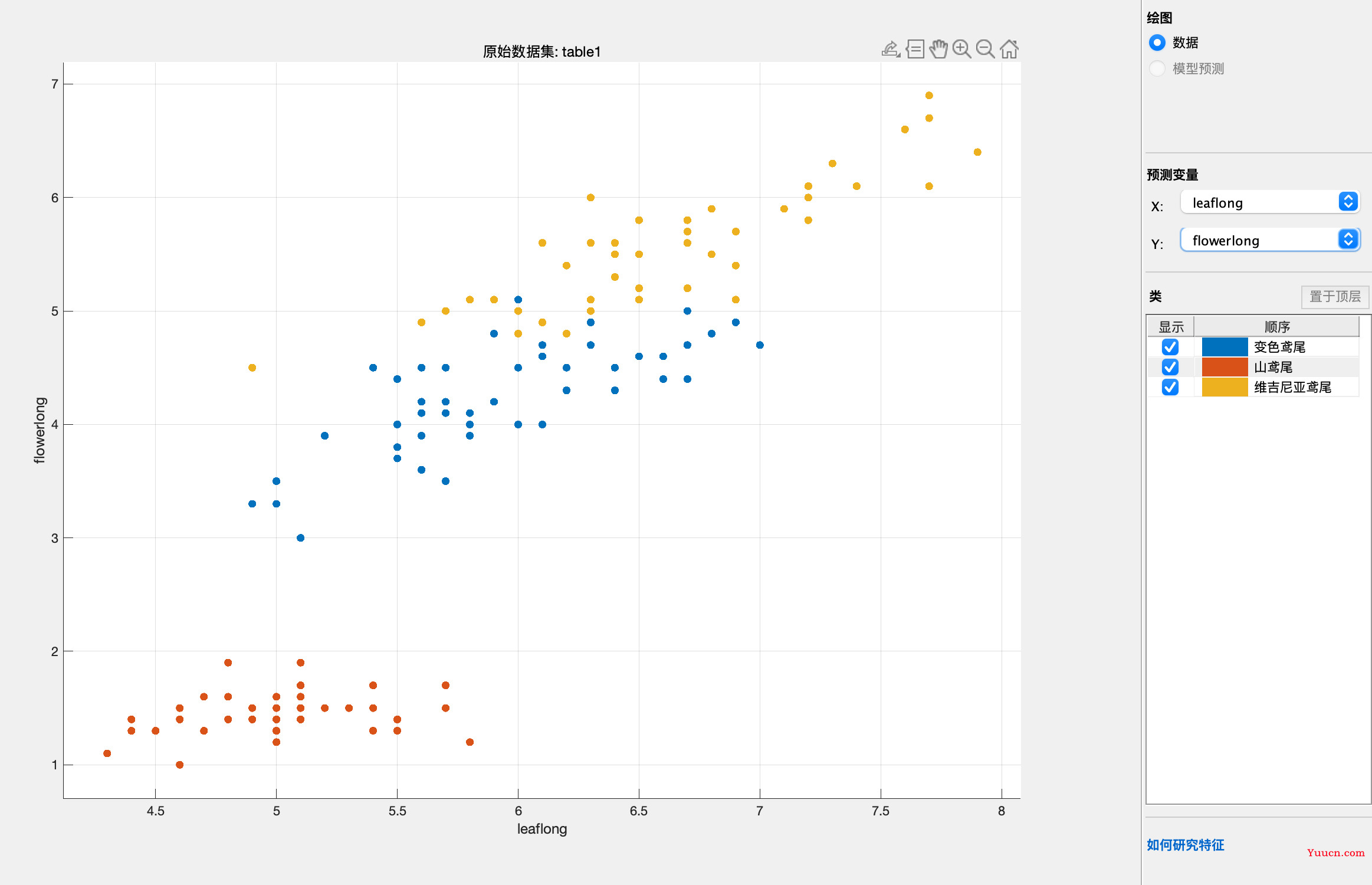
刚出来的结果是这样的，但是我们一般不用在意，除非区分的特别明显才可能用

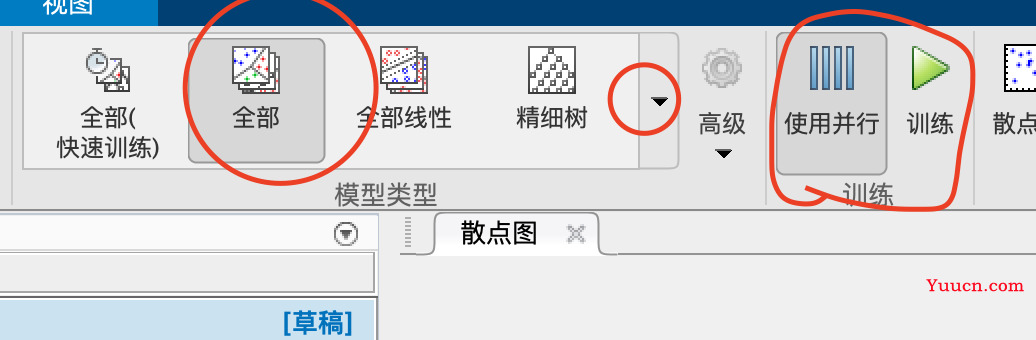
这里可以选择训练全部模型+使用并行+训练，可以快速使用多个模型

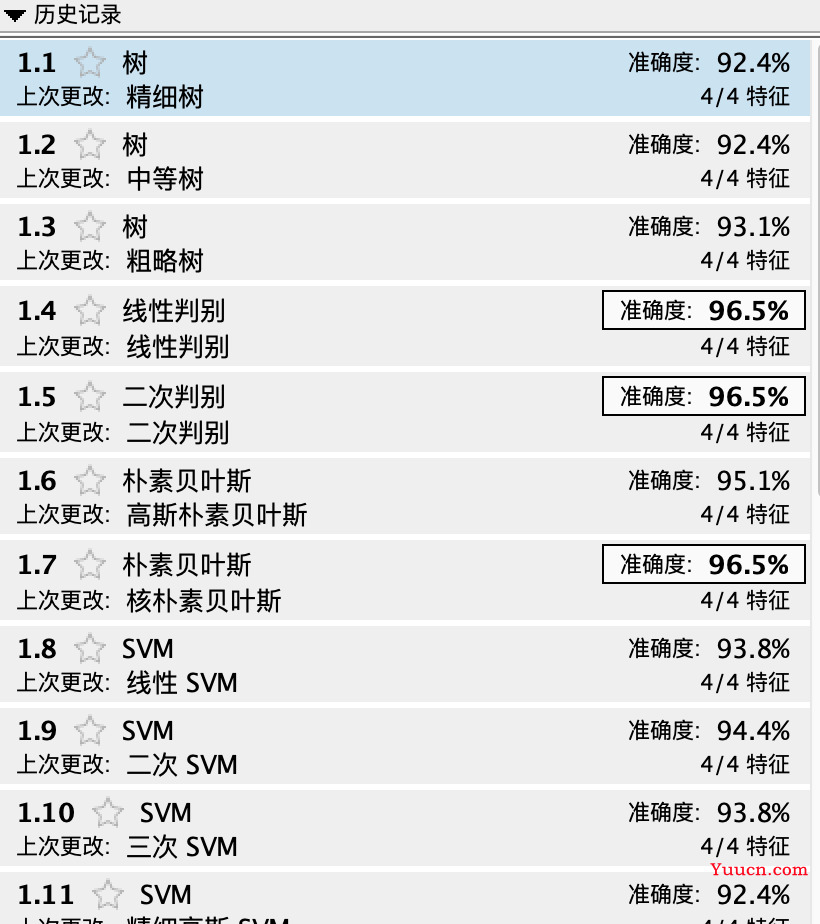
可以点每个模型看roc、混淆矩阵等，写入论文

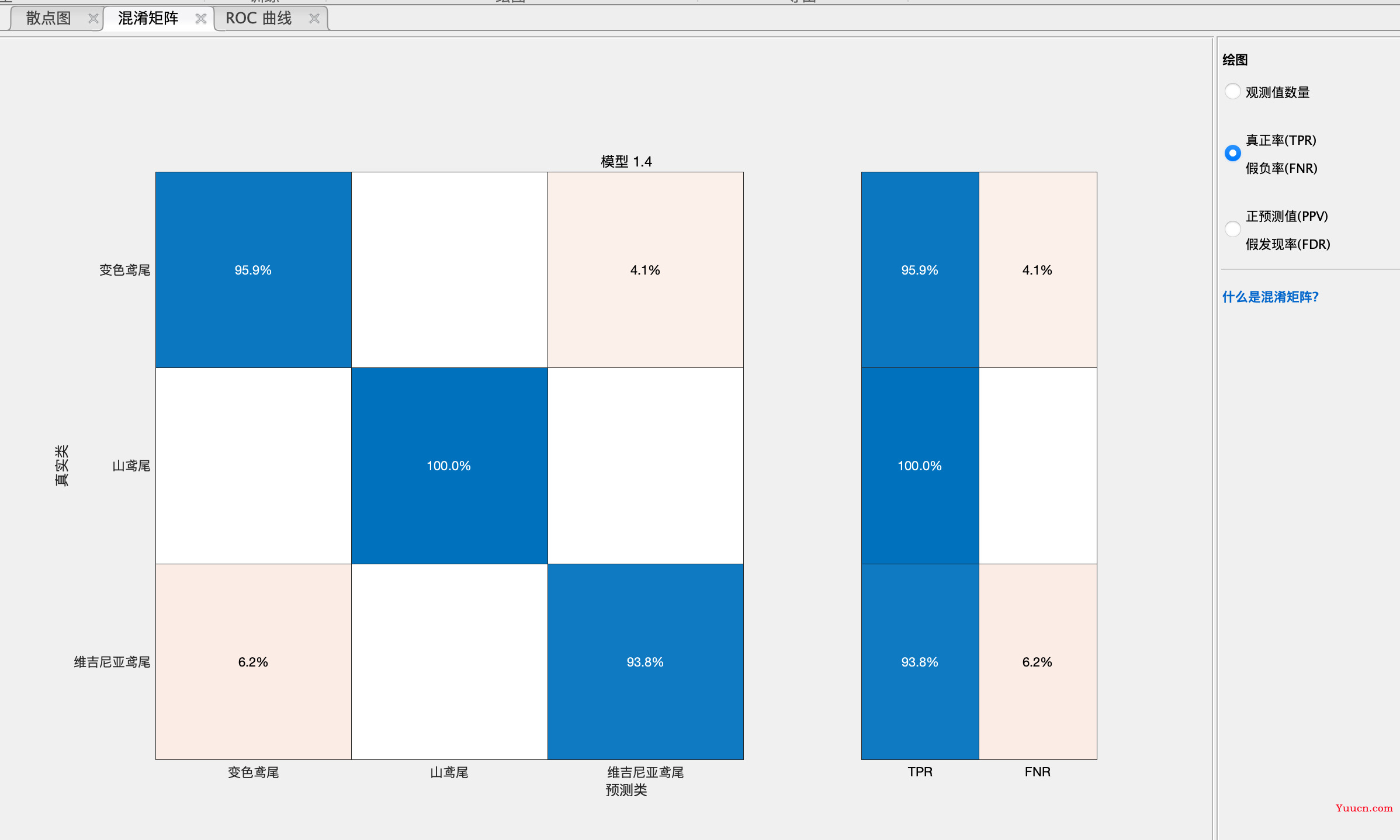
可以导出模型

Starting parallel pool (parpool) using the 'local' profile ...
Connected to the parallel pool (number of workers: 6).
变量已在基础工作区中创建。
从 Classification Learner 导出了结构体 'trainedModel'。
要对新表 T 进行预测: 
 yfit = trainedModel.predictFcn(T) 
有关详细信息，请参阅 How to predict using an exported model。

进行预测，导入需要预测的表

>>  yfit = trainedModel.predictFcn(table2)
yfit = 
  6×1 categorical 数组
     山鸢尾 
     维吉尼亚鸢尾 
     山鸢尾 
     变色鸢尾 
     维吉尼亚鸢尾 
     山鸢尾

导出代码进行预测

导出模型是比较简单傻瓜的办法，真正要调参的是需要导出代码进行修改的。

生成函数

第一行的函数声明不要

其他的复制进实时脚本中

比如

inputTable = trainingData;
predictorNames = {'VarName1', 'VarName2', 'VarName3', 'VarName4'};
predictors = inputTable(:, predictorNames);
response = inputTable.VarName5;
isCategoricalPredictor = [false, false, false, false];
% 训练分类器
% 以下代码指定所有分类器选项并训练分类器。
classificationTree = fitctree(...
    predictors, ...
    response, ...
    'SplitCriterion', 'gdi', ...
    'MaxNumSplits', 100, ...
    'Surrogate', 'off', ...
    'ClassNames', categorical({'变色鸢尾'; '山鸢尾'; '维吉尼亚鸢尾'}));
% 使用预测函数创建结果结构体
predictorExtractionFcn = @(t) t(:, predictorNames);
treePredictFcn = @(x) predict(classificationTree, x);
trainedClassifier.predictFcn = @(x) treePredictFcn(predictorExtractionFcn(x));
% 向结果结构体中添加字段
trainedClassifier.RequiredVariables = {'VarName1', 'VarName2', 'VarName3', 'VarName4'};
trainedClassifier.ClassificationTree = classificationTree;
trainedClassifier.About = '此结构体是从 Classification Learner R2020a 导出的训练模型。';
trainedClassifier.HowToPredict = sprintf('要对新表 T 进行预测，请使用: \n yfit = c.predictFcn(T) \n将 ''c'' 替换为作为此结构体的变量的名称，例如 ''trainedModel''。\n \n表 T 必须包含由以下内容返回的变量: \n c.RequiredVariables \n变量格式(例如矩阵/向量、数据类型)必须与原始训练数据匹配。\n忽略其他变量。\n \n有关详细信息，请参阅 <a href="matlab:helpview(fullfile(docroot, ''stats'', ''stats.map''), ''appclassification_exportmodeltoworkspace'')">How to predict using an exported model</a>。');
% 提取预测变量和响应
% 以下代码将数据处理为合适的形状以训练模型。
%
inputTable = trainingData;
predictorNames = {'VarName1', 'VarName2', 'VarName3', 'VarName4'};
predictors = inputTable(:, predictorNames);
response = inputTable.VarName5;
isCategoricalPredictor = [false, false, false, false];
% 执行交叉验证
partitionedModel = crossval(trainedClassifier.ClassificationTree, 'KFold', 5);
% 计算验证预测
[validationPredictions, validationScores] = kfoldPredict(partitionedModel);
% 计算验证准确度
validationAccuracy = 1 - kfoldLoss(partitionedModel, 'LossFun', 'ClassifError');

运行一下查看样本内预测结果：

使用模型进行对未知数据的预测
找到trainedClassifier.predictFcn
导入要预测的数据

trainedClassifier.predictFcn(data2)

补充：各个模型的中文

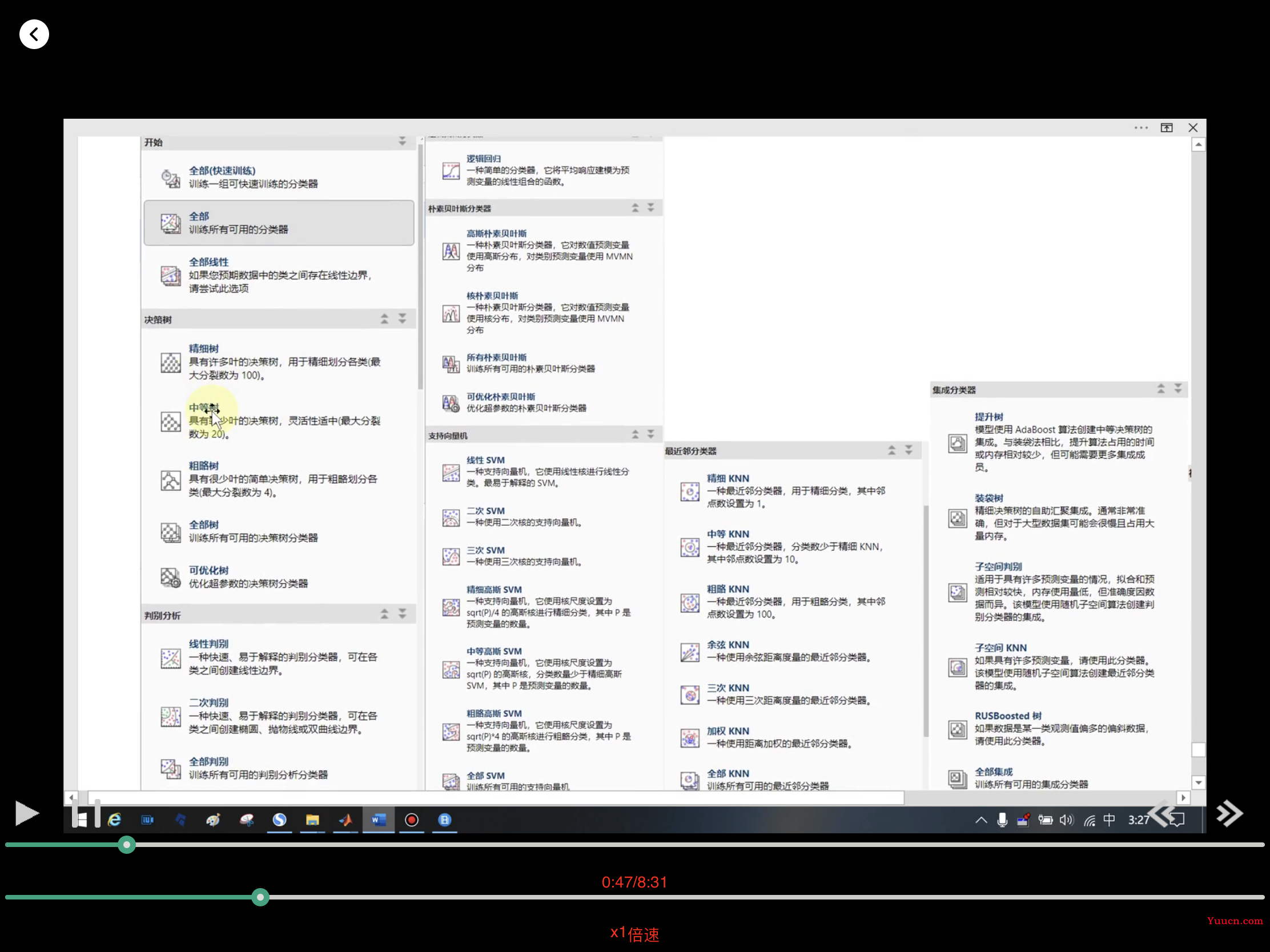
决策树预测和可视化

按上面的步骤，选用决策树模型，进行训练并导出代码

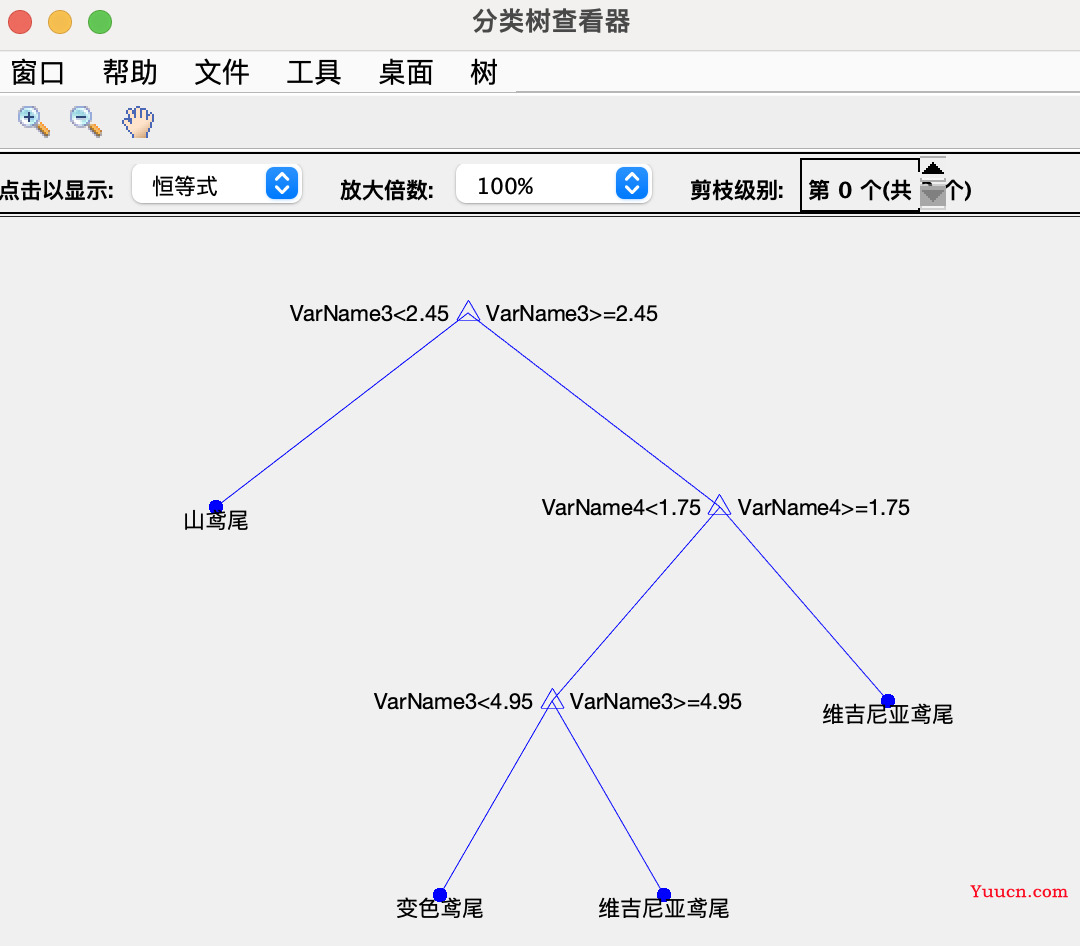
对于决策树模型，我们可以使用下面的代码将它可视化：

如果使用的导出模型：

view(trainedModel.ClassificationTree,'Mode','graph')

如果是生成函数：

view(trainedClassifier.ClassificationTree,'Mode','graph')

（如果图上节点太多，图会非常的丑，这时候就别放论文了）

trainedModel和trainedClassifier是默认的，会根据自己重新命名的名字而要重命名

交叉验证的测试集和随机数种子

学对于 K 折交叉验证

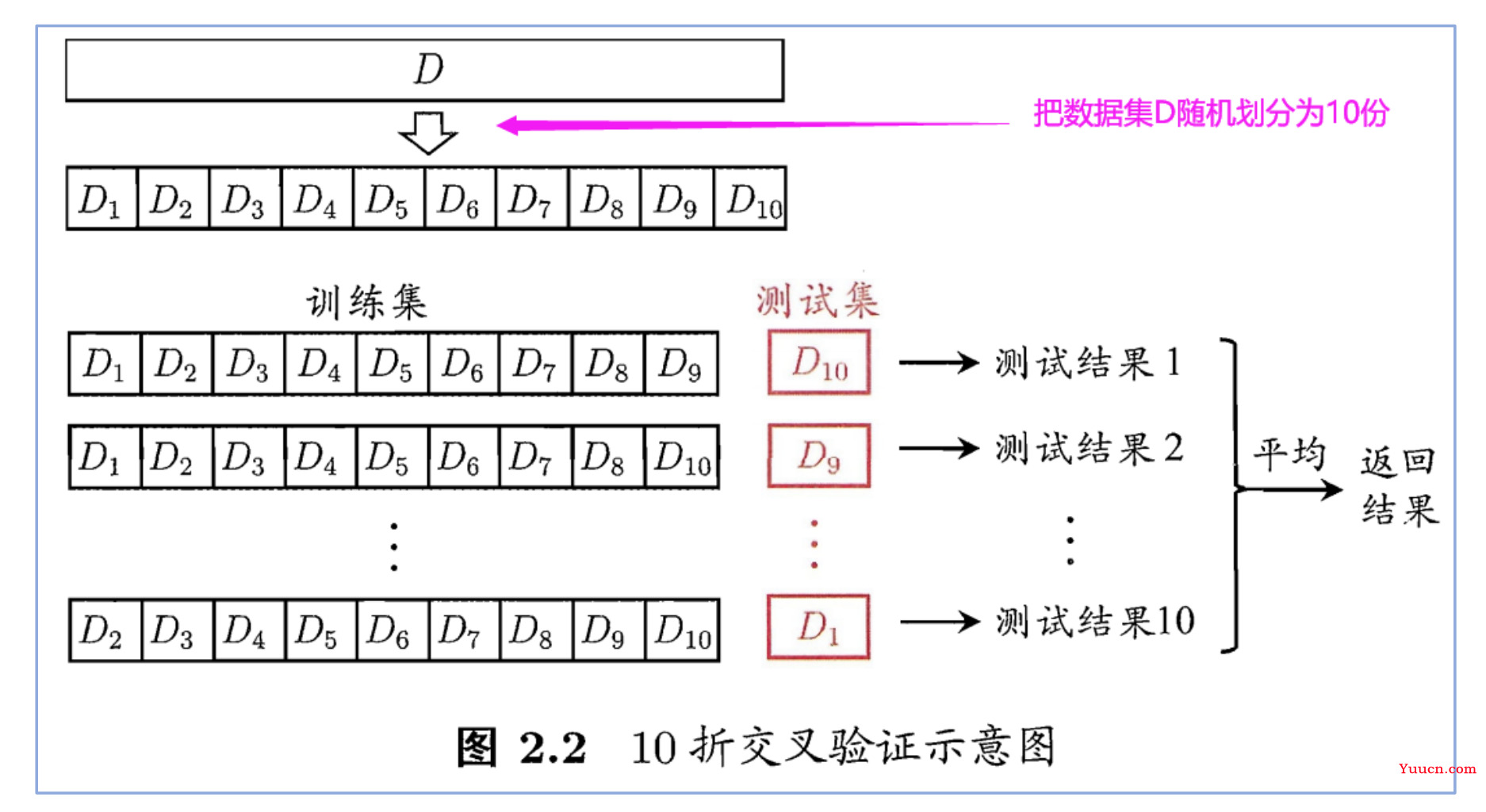
图上的“平均”两个字应该指的是对十次测试之后，对每次测试的参数求了均值，作为模型的参数。而不是把每次的结果平均。

我们进行交叉验证的目的是为了看我们的模型在测试集上的表现，即为了衡量模型的泛化能力。

在上面的 10 折交叉验证中，我们将这个模型训练了十次，每次的测试集都是新的，且每一个样本都会作为一次测试集，作为测试集时，MATLAB 会给我们返回它们的预测结果。

（每次测试集是全部的十分之一，十次训练完之后，刚好所有的样本都作为过测试集得到一次预测的结果，汇总起来刚好是完整的混淆矩阵）

因此经过交叉验证后，我们就能得到每个样本的预测结果，又由于我们知道每个样本它们的真实的结果，因此我们可以将所有样本预测的结果和真实的结果汇总成一个完整的混淆矩阵，然后通过这个混淆矩阵来计算我们所需要衡量的指标，例如分类准确率、f1 分数等。

代码中validationPredictions是测试集预测结果

response是真实结果

随机数种子

每次训练时，结果会不同。因为每次对训练集和测试集的划分，是随机的

此时可以用rng()固定随机数种子

比如将rng(100)写在最前面，就是将100最为随机数种子，无论多少次运行，对训练集和测试集的划分都是一样的

计算F1分数和AUC，绘制ROC曲线

多分类问题F1分数计算

二分类问题中的计算

F1是对查全率和查准率的调和平均数，属于是一个综合反应

多分类问题

多分类的 F1 分数分为两种，一种叫做 micro F1 **分数（**micro[ˈmaɪkroʊ]表示微观的），另一种叫做 macro F1 **分数（macro[ˈmækroʊ]**表示宏观的）。

和二分类的 F1 分数不同，micro F1 分数和 macro F1 分数不需要指定正类是什么，因为它们计算的是一个综合的分数。（二分类别用这两个 F1 分数，没见过有人在二分类用过它们）

micro F1 分数：
- 每个类别分别作为正类时，都可以算出来一组 TP、FP 和 FN 的值，我们把它们分别求和来计算所有样本的 TP、FP 和 FN，然后再套用 F1 分数的公式。
macro F1 分数，它有两种定义方法：
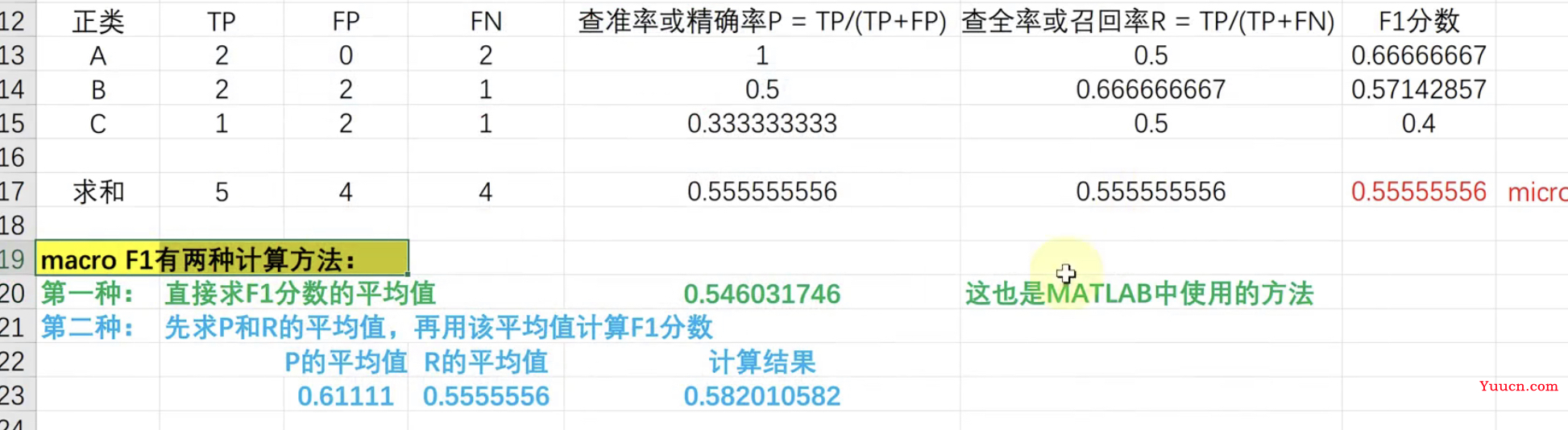
- **第一种：**先计算出每一类作为正类时的 F1 分数，然后对所有的 F1 分数求平均。（MATLAB和 Python 中用的都是这一种计算方法）
- **第二种：**先计算出每一类作为正类时的精确率 P 和召回率 R，然后分别计算 P 和 R 的平均值，再利用公式 $F_{1}=2\times\frac{P \times R}{P+R}$ 用该平均值计算 F1 分数。
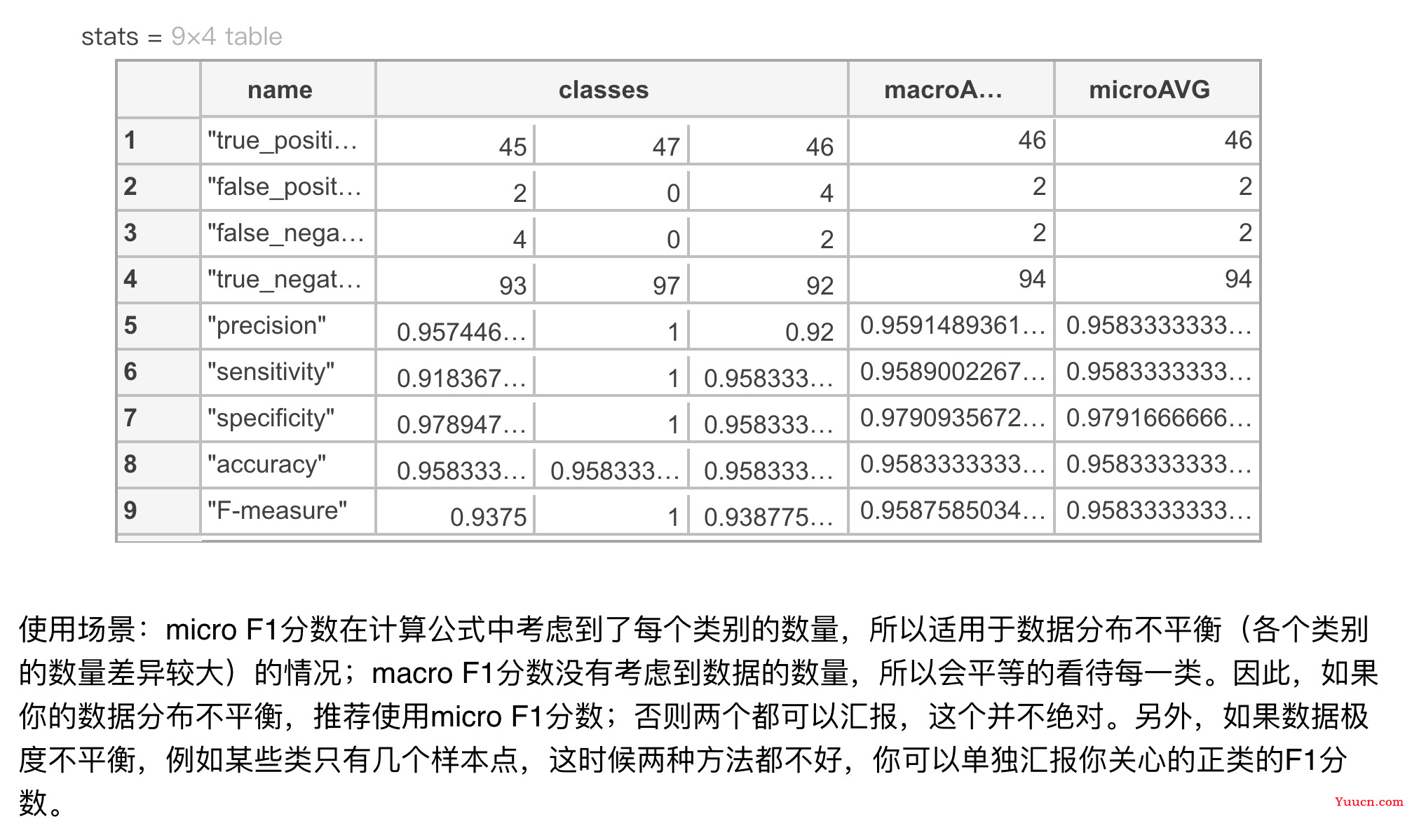
使用场景：
- micro F1 分数在计算公式中考虑到了每个类别的数量，所以适用于数据分布不平衡（各个类别的数量差异较大）的情况；macro F1 分数没有考虑到数据的数量，所以会平等的看待每一类。
- 因此，如果你的数据分布不平衡，推荐使用 micro F1 分数；否则两个都可以汇报，这个并不绝对。
- 另外，如果数据极度不平衡，例如某些类只有几个样本点，这时候两种方法都不好，你可以单独汇报你关心的正类的 F1 分数。
总结：样本不平衡用micro F1，平衡用macro F1。极度不平衡，只要计算关心的正类的F1即可

怎么看每一类的个数？ MATLAB 的 tabulate 函数可以帮你，具体可以看视频演示。

Matlab计算F1分数

function [stats] = statsOfMeasure(confusion)

资料中有这个函数，根据混淆矩阵可以计算一系列指标，比赛时直接用就行。

zs = {'A','A','A','A','B','B','B','C','C'}; % 真实的结果
yc = {'A','A','B','C','B','B','C','B','C'}; % 预测的结果
ClassNames = {'A','B','C'}; % 样本有几类
C = confusionmat(zs,yc,'Order',ClassNames) % 先计算混淆矩阵（order后面指定类的顺序）

出来的结果并不是很好看，所以可以用一个别人写的函数

% confusionchart(zs,yc)  % 混淆矩阵的可视化 R2018b版本才被引入

stats = statsOfMeasure(C)  % 调用我们下载的那个第三方的函数（函数要放到当前文件夹）

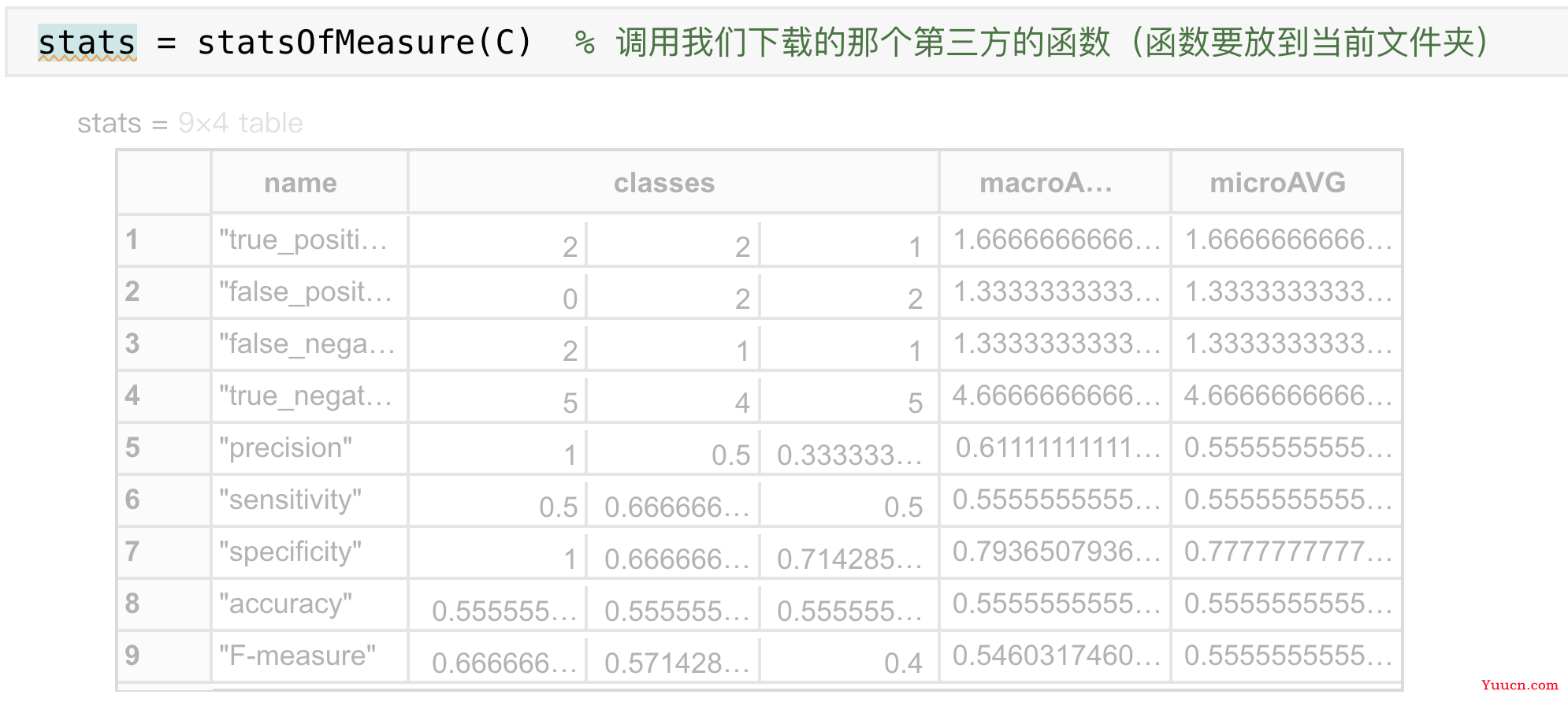
结果：最下面一行，分别是每一类的F1分数、宏观F1和微观F1

最左侧的name列从上到下分别是：

TP FP FN TN 查准率或精确率查全率或召回率特异性分类准确率 F1分数

最后两列分别是Macro F1和Micro F1，我们只用管它们最下面的那个元素，上面的元素可以忽略。

Macro F1 = 0.54603 ; Micro F1 = 0.55556

因为我们是三分类问题，所以classes下面有三列，分别表示当正类为ClassNames中的某个元素时，其对应的衡量指标。

关于这个第三方函数的使用：

先导出训练好的模型代码

开头改变训练的数据trainingData = data1;

下面就是利用交叉验证预测的结果和真实的结果来计算F1分数

提取出因变量中所有的分类

ClassNames = unique(response) % y中各类的名称

创建混淆矩阵，调用函数
混淆矩阵第一个参数是真实值，第二个是预测值（导出的代码中有），第三个参数是顺序，即规定的类别

group = response;  % y所在的那一列（真实的类别）
C = confusionmat(group,validationPredictions,'Order',ClassNames); % 先计算混淆矩阵
stats = statsOfMeasure(C)  % 调用我们下载的那个第三方的函数

调用描述性统计的函数，观察样本分布是否平均

tabulate(response)  % 查看每一类的样本量

需要提取表里面的宏观和微观F1分数

Macro_f1_score = stats.macroAVG(end) % macro:宏观

Macro_f1_score =

0.958758503401361

Micro_f1_score = stats.microAVG(end) % micro:微观

如果你关心某一类的F1分数，可以使用下面的代码得到它对应的F1分数

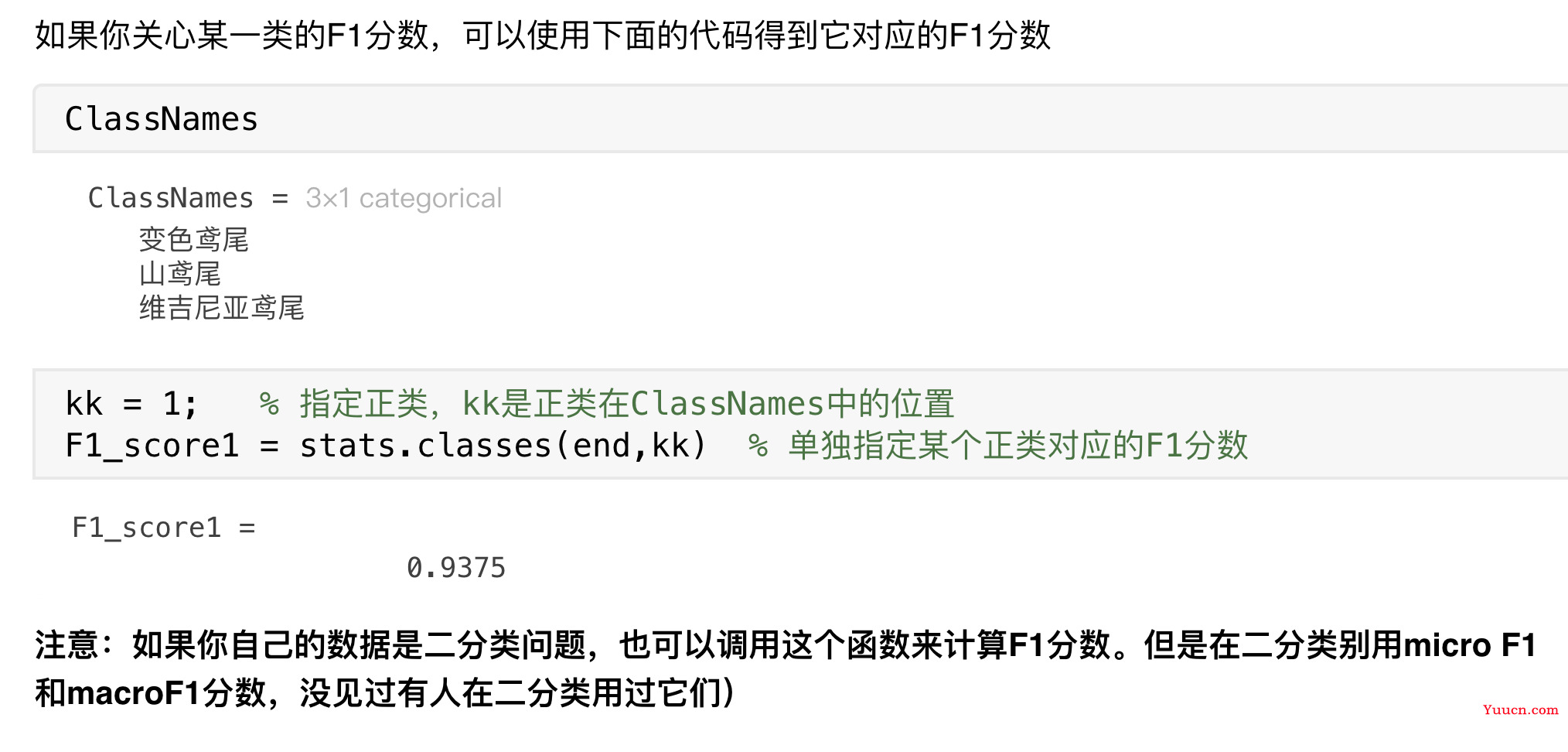
kk = 1;   % 指定正类，kk是正类在ClassNames中的位置
F1_score1 = stats.classes(end,kk)  % 单独指定某个正类对应的F1分数

注意：如果你自己的数据是二分类问题，也可以调用这个函数来计算F1分数。但是在二分类别用micro F1和macroF1分数，没见过有人在二分类用过它们）

ROC曲线与AUC曲线

ROC 曲线： 根据一系列不同的分类阈值，以真正类率(True Postive Rate, TPR)为纵坐标，假正类率（False Positive Rate, FPR）为横坐标绘制的曲线。（原理有兴趣的同学可以在 b 站搜索相关的视频）

ROC 曲线的用法： 将不同的模型的 ROC 曲线绘制在同一张图内，最靠近左上角的那条曲线代表的模型的分类效果最好。

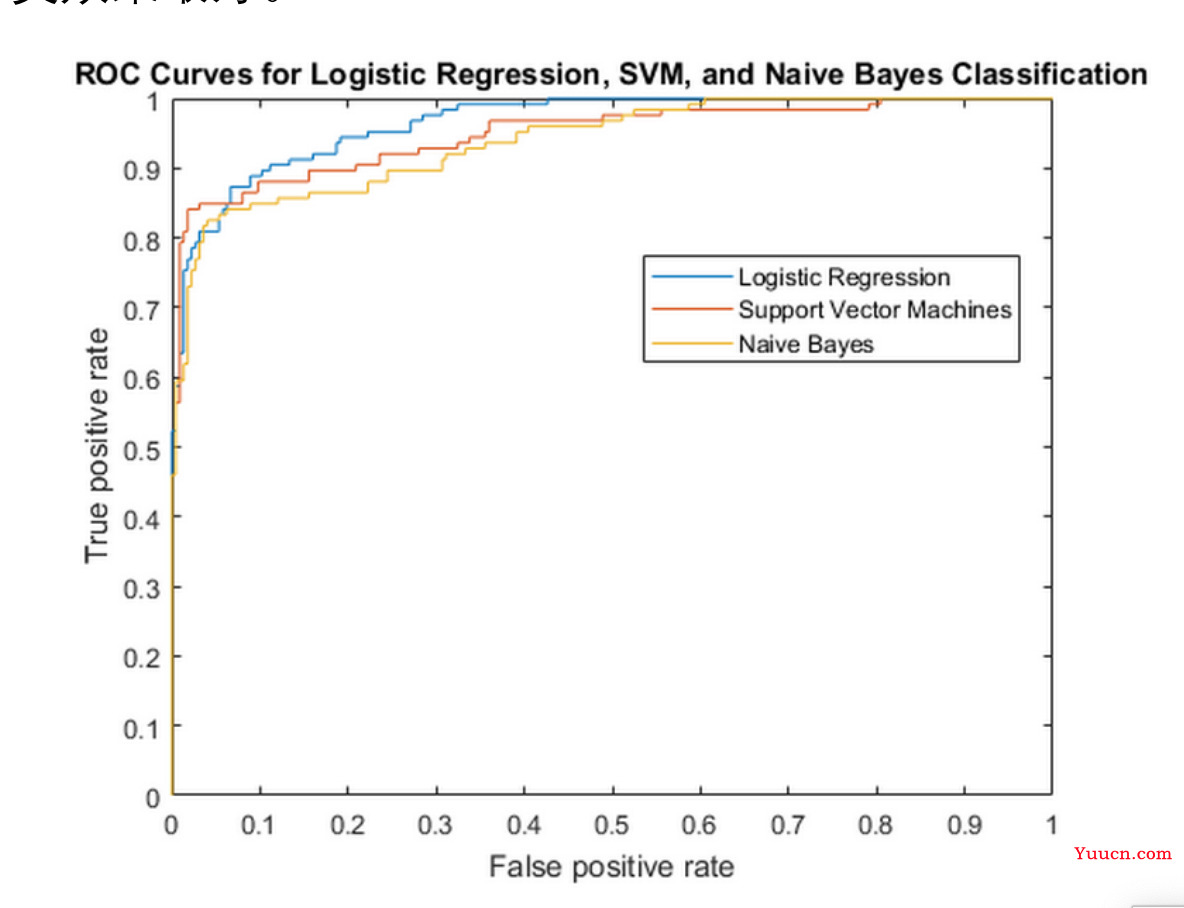
Tips:比较多个模型时，训练集和测试集的划分要一致，可以用 rng 函数固定随机数种子

缺点： 实际任务中，情况很复杂，如果两条 ROC 曲线发生了交叉，则很难一般性地断言谁优谁劣。

AUC： AUC 被定义为 ROC 曲线与下方的坐标轴围成的面积，AUC 的范围位于[0,1]之间，AUC 越大则模型的分类效果越好，如果 AUC 小于等于 0.5，则该模型是不能用的。通常AUC 大于 0.85 的模型就表现可以了。（当然这种标准不绝对，具体问题具体分析）

我们要选好正类是哪一个

注意，ROC 曲线和 AUC 不区分二分类和多分类问题，但我们需要选好正类是哪一个，不同的正类对应的 ROC 曲和 AUC 不同。在 matlab 中我们可以使用 perfcurve 函数进行计算，它的使用方法有点复杂，请看视频演示。

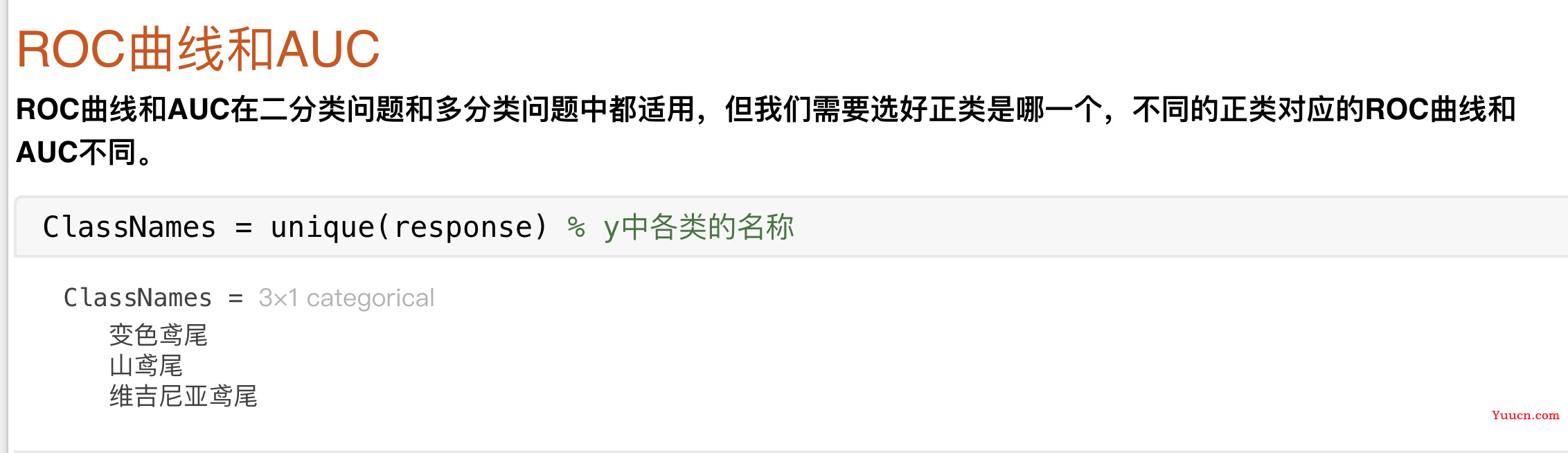
kk = 1;   % 指定正类，kk是正类在ClassNames中的位置
posclass = ClassNames(kk); % 正类的名称
group = response;  % y所在的那一列（真实的类别）
% validationScores是我们运行上面导出的代码得到的预测的分数（这个分数在不同的模型中代表的含义不同）
[x_roc,y_roc,~,auc] = perfcurve(group,validationScores(:,kk),posclass); % 第三个输出参数我们不需要，所以这里写成~
% ~是连接号的波浪线符号,在Tab键的上面  
figure(3)
plot(x_roc,y_roc)
xlabel('假正类率FPR'); ylabel('真正类率TPR');

[x_roc,y_roc,~,auc] = perfcurve(group,validationScores(:,kk),posclass);

group是真实的类别，y所在的那一列
validationScores(:,kk)是正类所在那一列的预测得分（这个分数在不同的模型中代表的含义不同）
posclass是正类名称
返回值
- x_roc横坐标
- y_roc纵坐标
- ~表示不需要第三个参数
- auc计算出来的auc值

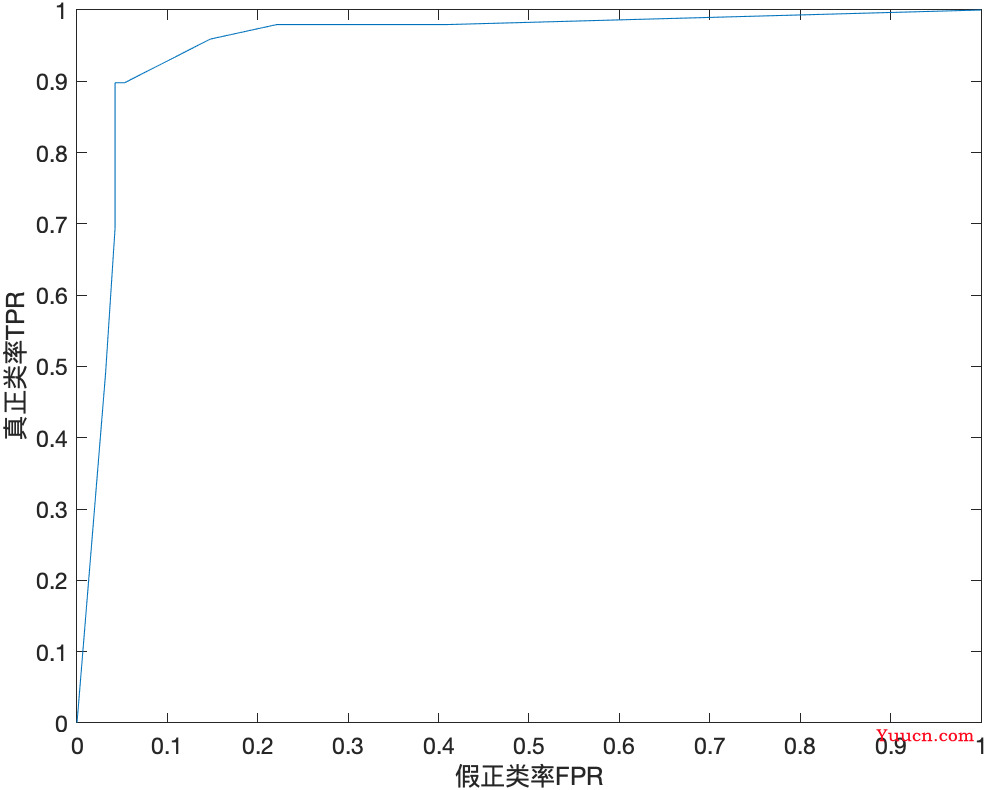
对同个数据使用不同模型得到的ROC曲线放同一个图片中

就是把不同模型的代码导出来，固定相同的随机数种子（保证测试集和预测集划分一致）。使用同样的数据进行训练，然后

ClassNames = unique(response) % y中各类的名称
kk = 1;   % 指定正类，kk是正类在ClassNames中的位置
posclass = ClassNames(kk); % 正类的名称
group = response; 
[x1,y1,~,auc1] = perfcurve(group,validationScores(:,kk),posclass);

获得画ROC曲线的横纵坐标以及AUC值，将其命名，以免跟后面重复。

然后我们可以选另一个模型，进行同样的训练操作。(仅展现最后步骤)

[x2,y2,~,auc2] = perfcurve(group,validationScores(:,kk),posclass); % 第三个输出参数我们不需要，所以这里写成~

画图

figure(4)
plot(x1,y1,'r','linewidth',2)  % 红色、线宽为2
hold on  % 继续在当前图上绘图
plot(x2,y2,'b','linewidth',2)   % 蓝色、线宽为2
xlabel('假正类率FPR'); 
ylabel('真正类率TPR');
text1 = ['决策树, AUC = ', num2str(round(auc1,4))];
text2 = ['SVM, AUC = ', num2str(round(auc2,4))]; % round是取小数点后四位，显示上好看一些
% "决策树, AUC = " + round(auc1,4); % MATLAB2017a版本才支持双引号的字符串
legend(text1,text2) % 加上图例

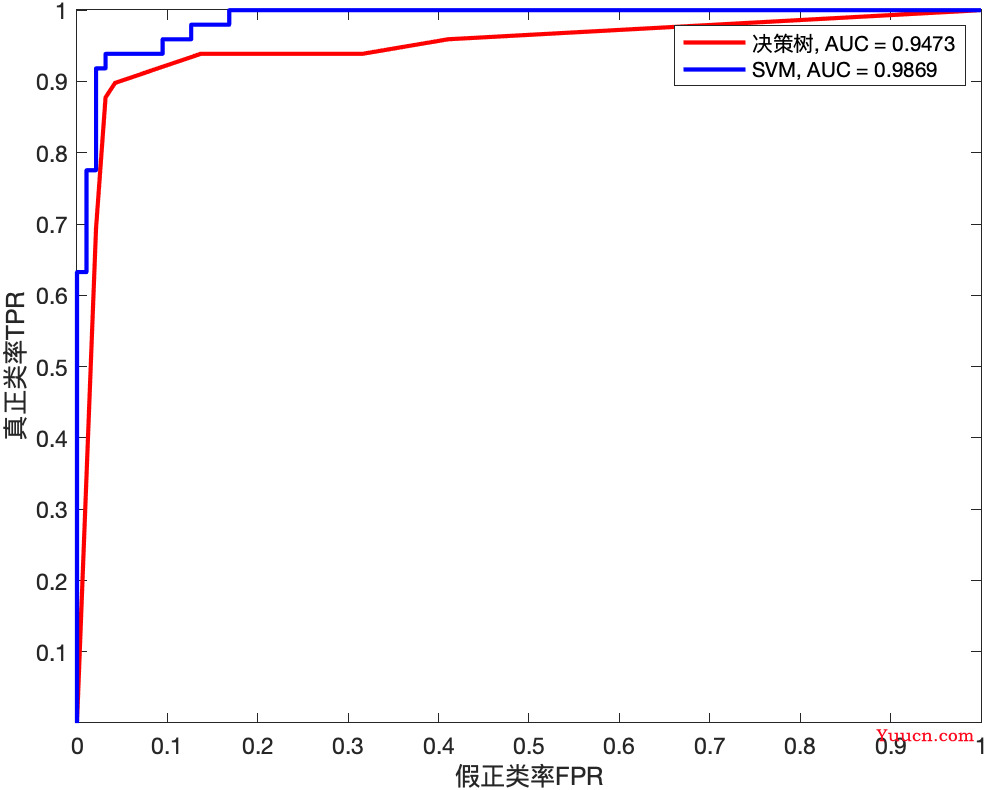
这里是将正类指定为变色鸢尾，如果将正类指定为山鸢尾，可能会得到相反的答案
所以说多分类问题我们最好用宏观/微观F1分数判断，省去指定正类的麻烦

网格搜索调参

关于调参

调参的定义

调参即对模型的参数进行相应的调整，以期获得更好的预测效果！

其中参数又分为：模型参数和模型超参数。

模型参数：
- 模型内部的配置变量，可以用数据估计模型参数的值。比如线性回归或逻辑回归中的系数。它们会在模型训练过程中自动被计算出来，因此我们不需要管。
模型超参数：
- 模型外部的配置，必须手动设置参数的值，其值不能从数据估计得到，比如K 近邻分析的 K，随机森林中决策树的个数。

总结：模型参数是在训练过程中从数据中自动估计的，而模型超参数是需要手动设置的。因此，调参调整的是模型中的超参数

调参的目的

调参调参，无非就是将模型的超参数调整到最佳的那个值，使得模型预测的效果最好。

怎么去衡量预测效果的好坏呢？我们可以指定一些可用来衡量模型的泛化能力的指标。例如，在分类问题中，我们可以使用 F1 分数或者 AUC 指标，我们要找到一组超参数使模型的在测试集上的 F1 分数或者 AUC 指标最高。

Matlab机器学习可以调的参数

以决策树为例

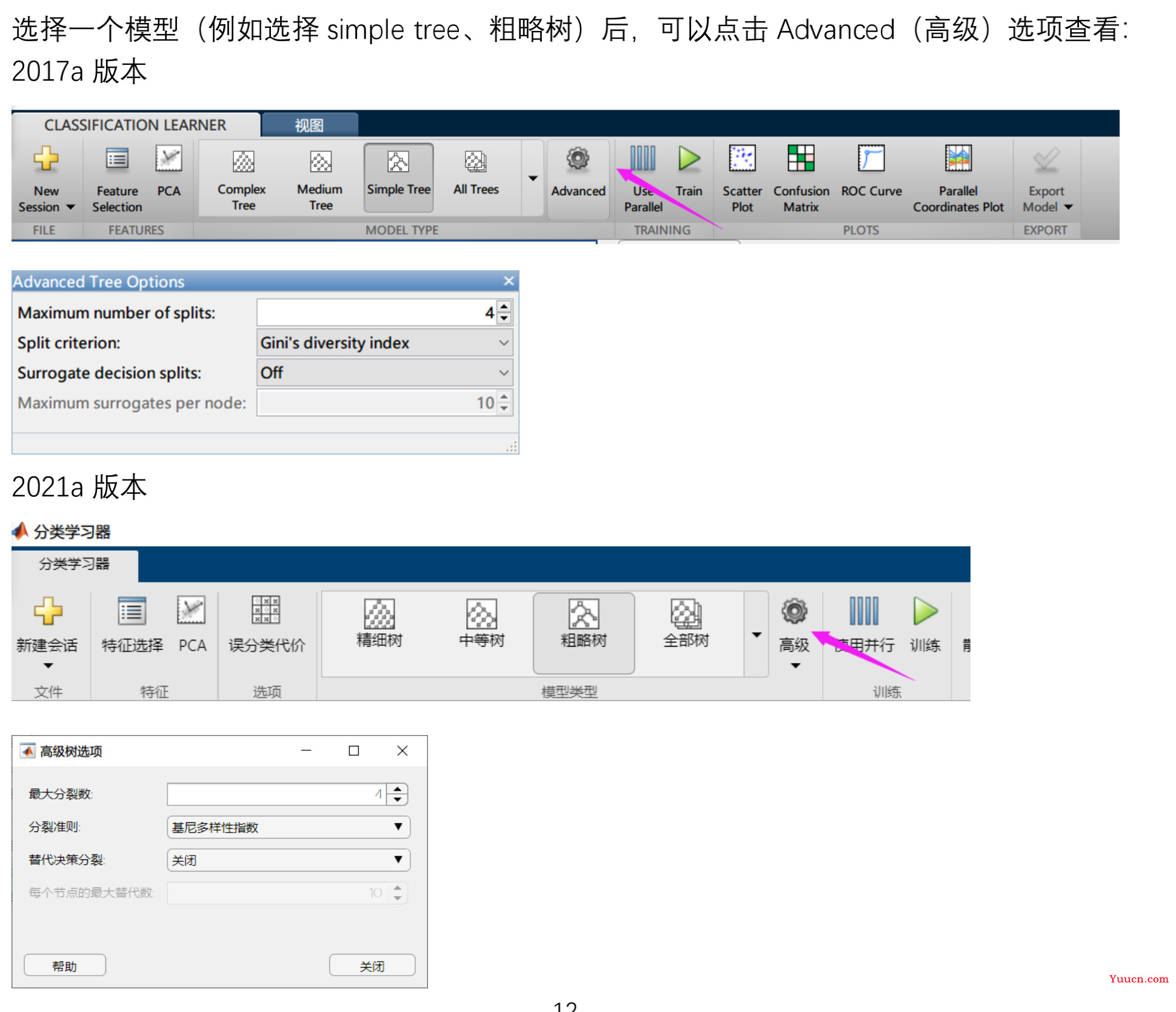
不同模型的超参数不同
要弄懂超参数的解释，必须要学习模型的理论推导

调参的方法

总的来说，常见的调参方法有下面三种：

网格搜索

在指定的参数范围内，遍历每一种可能的情况，看哪组参数能使得模型的效果最好。（类似于枚举法）

（1）有些参数只存在少数几种可能，例如下面决策树中的分裂准则中有三个选项可以选择。

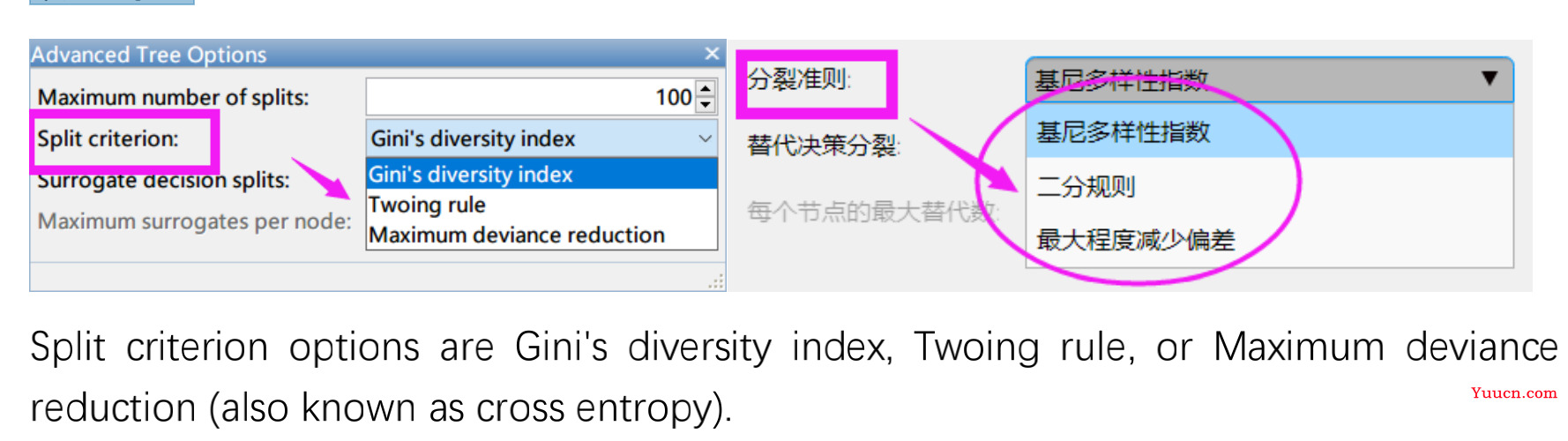
（2）有些参数存在的可能性非常多，甚至有无数种可能。例如最大分裂数，我们可以取任意一个正整数。

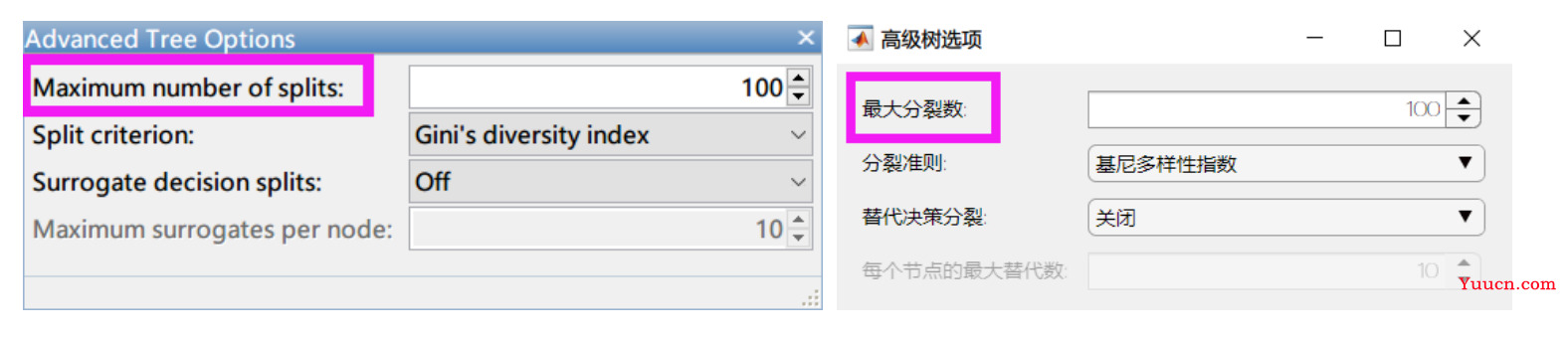
这种情况下我们可以根据经验给定一个指定的搜索范围，并指定一个搜索的步长。如果你学过决策树的理论，你就会知道决策树的最大分裂数不会超过样本个数。

假设现在样本个数为 500 的话，我们可以让最大分裂数从 1 开始取，每次增加 1（步长为 1），一直到 500 为止，这样会有 500 种不同的情况。

大家可以想一下，如果每次训练平均需要 1 分钟，那么调整这个参数需要训练 500 次，要等几个小时。。。如果你还需要同时考虑三种不同的分裂准则，那么需要训练3*500=1500 次。。。这种情况下我们可以减少要搜索的范围，例如给定一个较大的步长，将最大分裂数分别设置为[10 20 30 … 490 500]进行搜索。这样得到的模型可能会比上面差一点，但是时间却缩短到原来的 1/10.

思考：怎么编程实现网格搜索？（用循环，有几个参数要搜索就是几层循环）

**网格搜索的优点：**只要搜索的足够多，每种情况都尽量考虑到的话，我们有很大的可能性能找到最好的模型。
网格搜索的缺点：当要搜索的超参数比较多的时候，十分消耗计算资源和时间。

随机搜索

随机的在参数空间中进行采样（类似于蒙特卡罗模拟的思想）

Bergstra 和 Bengio 两位学者在他们 2012 年发表的文章中，表明随机搜索比网格搜索更高效。在牺牲一些预测的准确性后，可以大大缩短搜索的时间。

参考论文：Bergstra J, Bengio Y. Random search for hyper-parameter optimization[M].JMLR.org, 2012.

贝叶斯调参

一种启发式的调参策略（调参过程中用到了历史信息）

启发式：像模拟退火、遗传算法那样，用到了原来的信息

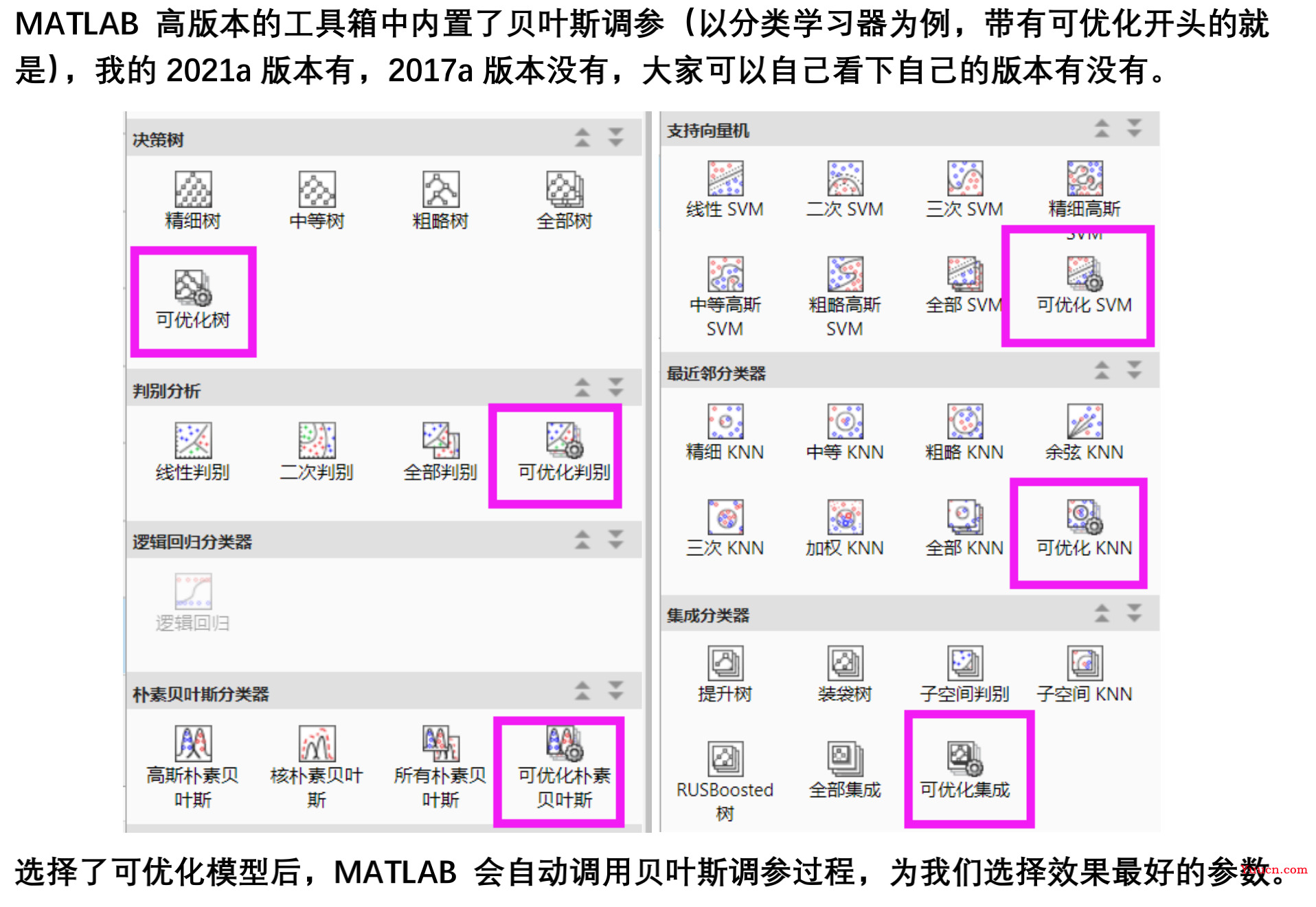
带**“可优化”**的模型，会自动调用贝叶斯搜索。

事实上，如果要调的参数不多的话，网格搜索仍然是用的最普遍的调参方法。

下面我们就以网格搜索为例，教大家对决策树进行调参，请看视频演示。

网格搜索调参演示

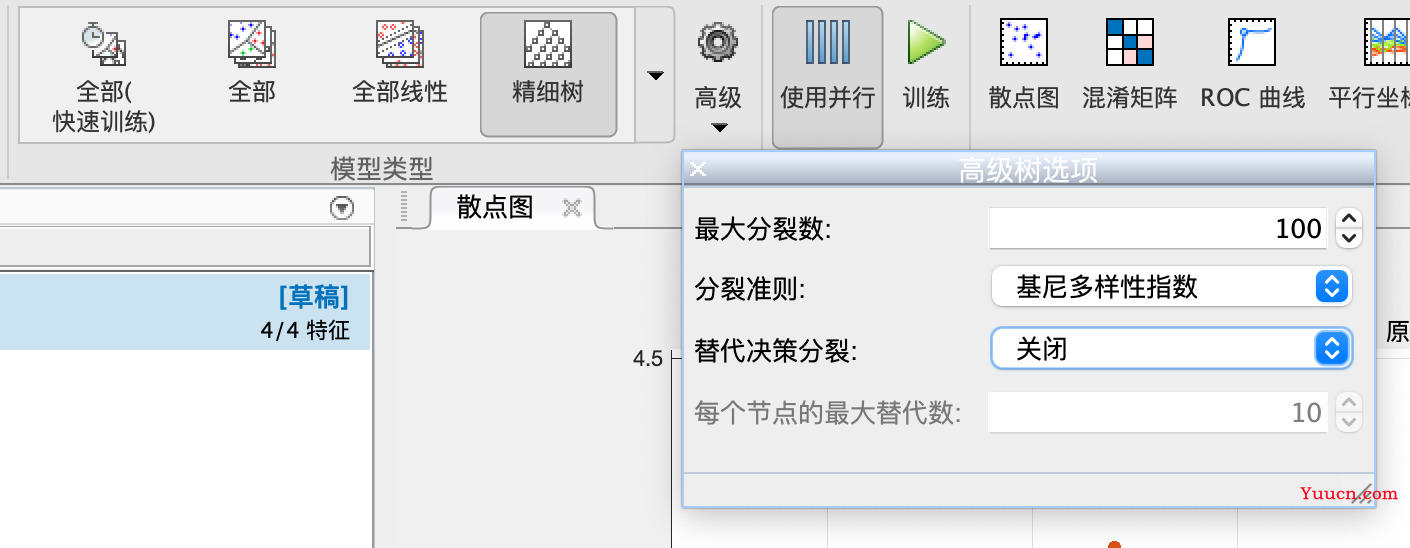
导入数据和打开一个决策树模型

我们这里只要调前两个参数，因为替代决策分类大概是对缺失值的处理，这里不需要调

开始操作

生成函数，将输入数据，改为我们自己的变量

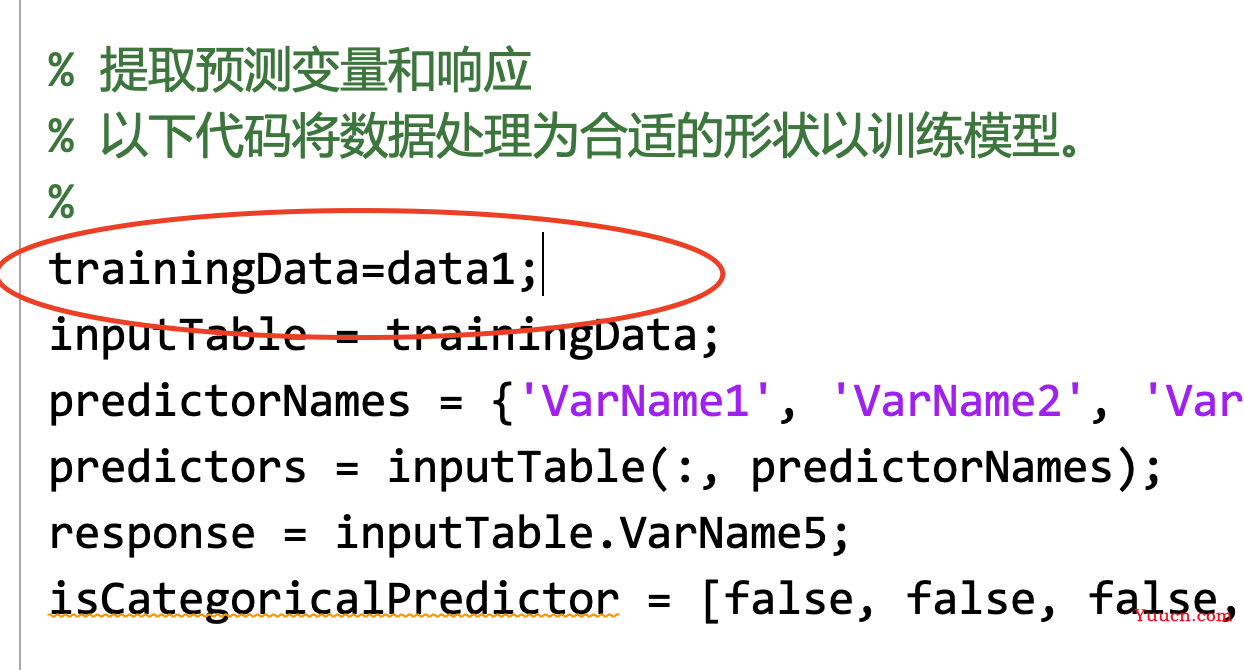
模型的参数在这里，我们要给出这些参数的范围

怎么找呢，我们先打开这个训练函数，如图中的fitctree，右键打开”fitctree“

ctrl/command+f，打开搜索，搜索参数名字，比如“SplitCriterion”。找到后发现这个参数有三种选择

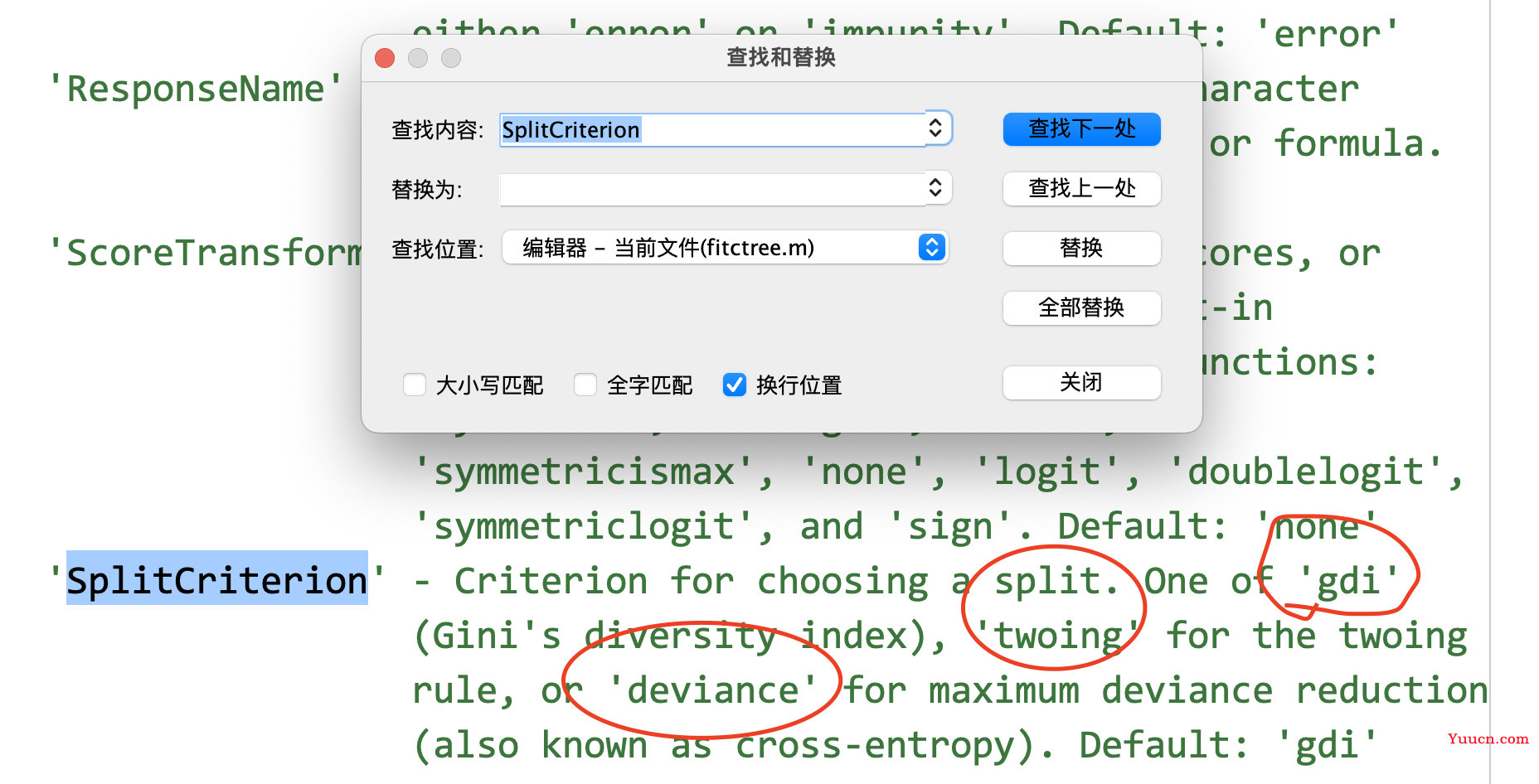
我们复制出来，用一个变量保存

SplitCriterion = {'gdi','twoing','deviance'}; %分裂准则有三个可以选的，这里用元胞数组保存

第二个参数，是一个数值型的，可以根据经验大致给一个范围
退出fitctree函数时不要保存，因为这是内部写好的
然后我们对代码写几层循环就行了

开头先设置一系列训练的数据

trainingData = data1;
inputTable = trainingData;
predictorNames = {'VarName1', 'VarName2', 'VarName3', 'VarName4'};
predictors = inputTable(:, predictorNames);
response = inputTable.VarName5;
isCategoricalPredictor = [false, false, false, false];
% 下面这两个变量在计算F1分数时会用到
ClassNames = unique(response); % y中各类的名称
group = response;  % y所在的那一列（真实的类别）

一个两重循环，一层循环是对一个参数的遍历

要固定随机数种子！！，每次训练集和测试集划分一样

存储每次循环的微观F1分数，用于确定最终的模型

（为了方便，这里添加了一个进度条）

SplitCriterion = {'gdi','twoing','deviance'}; %分裂准则有三个可以选的，这里用元胞数组保存
MaxNumSplits = 1:30;  % 最大分裂数（因为这个问题比较简单，我这里搜索设置的最大分裂数的上界是30）
num_i = length(SplitCriterion);  % 第一个超参数SplitCriterion的可能性有3种
num_j = length(MaxNumSplits);  % 第二个超参数MaxNumSplits的可能性有30种
MICRO_F1_SCORE = zeros(num_i,num_j); % 初始化最后得到的结果（初始化是为了加快代码运行速度）
mywaitbar = waitbar(0);   % 设置一个进度条
TOTAL_NUM = num_i*num_j;  % 总共要计算多少次
now_num = 0; % 已经计算了多少次
for i = 1:num_i
    for j = 1:num_j
        rng(520)  % 设定随机数种子，保证结果的可重复性(这里的520也可以换成其他的数字)
        %   注意，如果超参数是字符类型的话，它是被保存在元胞数组中的，取出时需要使用大括号才能得到字符型
        classificationTree = fitctree(...
            predictors, ...
            response, ...
            'SplitCriterion', SplitCriterion{i}, ...
            'MaxNumSplits', MaxNumSplits(j), ...
            'Surrogate', 'off', ...
            'ClassNames', categorical({'变色鸢尾'; '山鸢尾'; '维吉尼亚鸢尾'}));
        %% 中间时一系列模型的代码，直接复制即可，这里省略
     % 下面就是计算每一次循环得到的micro F1分数
        C = confusionmat(group,validationPredictions,'Order',ClassNames);
        stats = statsOfMeasure(C);
      MICRO_F1_SCORE(i,j) = stats.microAVG(end);
        % 更新进度条
        now_num = now_num+1;
        mystr=['计算中...',num2str(100*now_num/TOTAL_NUM),'%'];
        waitbar(now_num/TOTAL_NUM,mywaitbar,mystr);
    end
 end

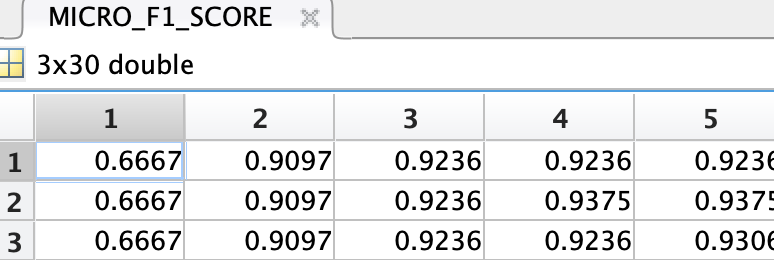
找最大的微观F1

best_micro_f1_score = max(MICRO_F1_SCORE(:))
[r,c] = find(MICRO_F1_SCORE == best_micro_f1_score,1); % 找到第一次出现最大值的行索引和列索引,根据索引找到最佳的参数
best_SplitCriterion = SplitCriterion{r} % 分裂准则，元胞数组用大括号取出元素
best_MaxNumSplits = MaxNumSplits(c)  % 决策树的最大分裂数

用热力图来实现可视化

figure(5)  % 画一个热力图
heatmap(MaxNumSplits,SplitCriterion,MICRO_F1_SCORE)

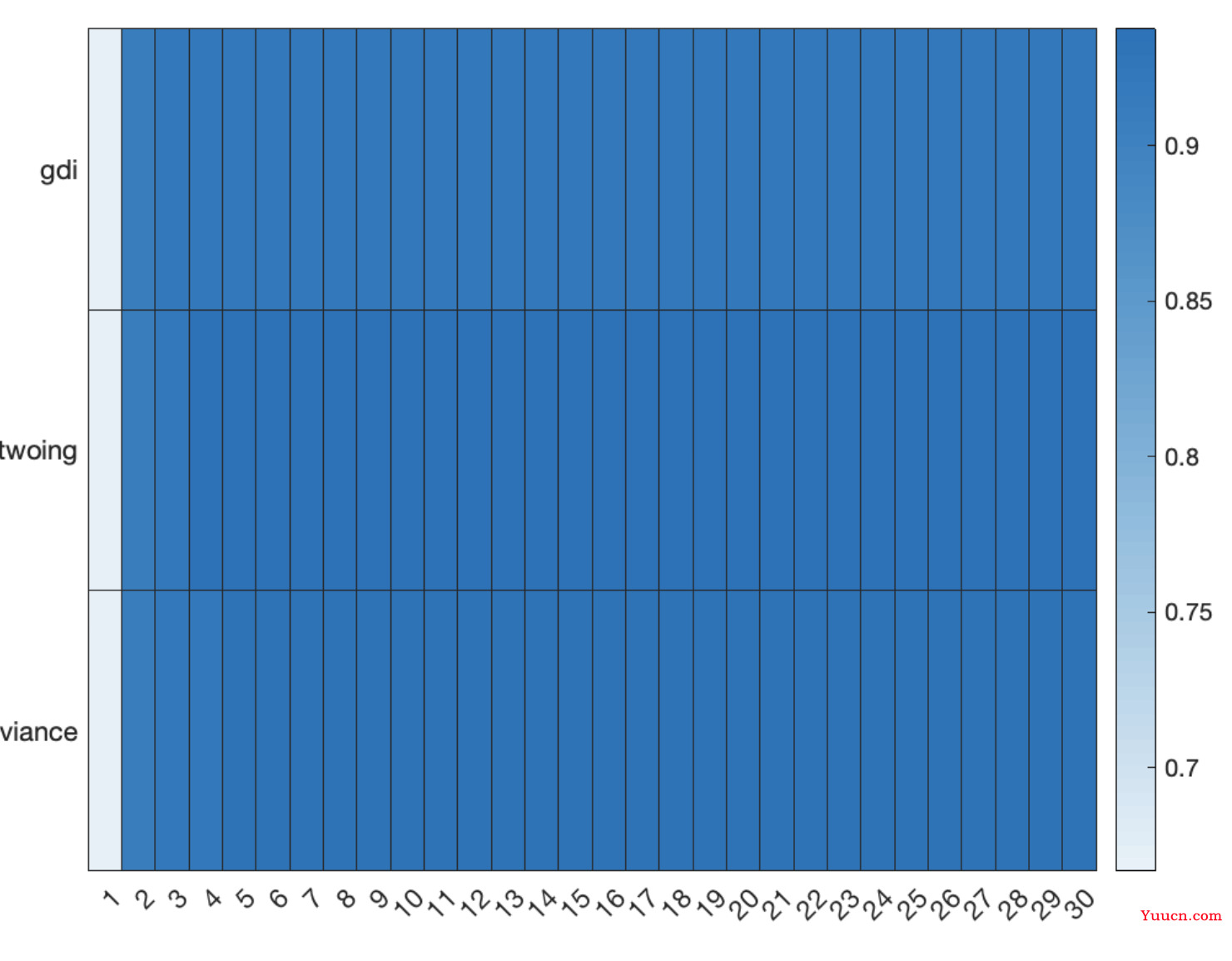
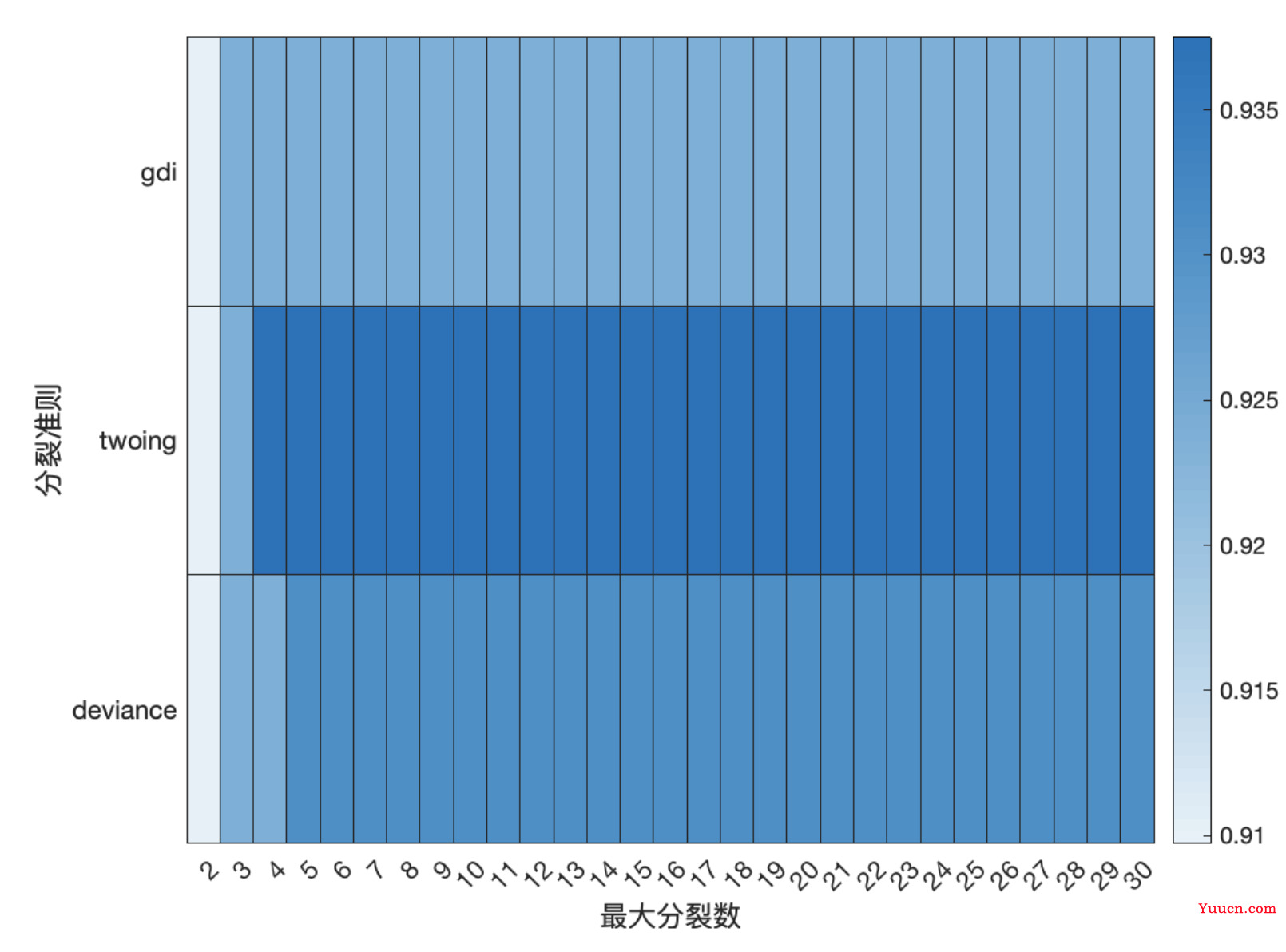
因为第一个变量列相比其他太小了，效果不好，所以去掉第一列

figure(6) % 第一列和其他相比太小了 去掉第一列重画
h_graph = heatmap(MaxNumSplits(2:end),SplitCriterion,MICRO_F1_SCORE(:,2:end));
h_graph.XLabel = '最大分裂数';
h_graph.YLabel = '分裂准则';

阶段性总结：模型选择的一般步骤

思路：通过交叉验证比较不同模型在测试集上的表现，选择效果最好的模型。

衡量的指标：

分类问题：AUC 、F1 分数、分类正确率等
回归问题：RMSE、MSE 等

不同模型有两层意思：

（1）模型完全不一样，例如 KNN、支持向量机、随机森林等

（2）模型名称相同，但是参数设置的不同。例如 KNN 中 K 取不同的值可以得到不同的模型。

因此我们选择最优的模型可以分成两步走：

（1）先单独对每个模型进行调参，得到使这个模型表现最好的那一组参数；

（2）比较在最优的参数下，这些模型在测试集上的表现。

这样做存在的问题：（1）将每个模型都调到最好的参数的时间会很长。（2）如果你在论文中将每个模型都介绍一遍的话，会显得内容太冗长了！

因此，在实际操作中，我们往往可以先使用 MATLAB 的机器学习工具箱把所有模型都尝试训练一次，缩小模型选择的范围，然后选择一至两个表现较好的模型进行调参。

这样我们得到的最终模型的表现效果也不会和上面的最优模型差的太大。

(事实上 MATLAB 训练所有的模型中，已经对部分模型设置了不同的超参数，只不过设置的有点粗糙而已)

另外，写论文的时候，重点介绍你最后选择的这个模型即可，其他的模型不要介绍的太详细，简单提一些就行了。

从参加数学建模比赛的角度来说，你还要想到评委老师是不是对这个模型熟悉。如果传统的模型表现也不错的话，尽量选择传统的模型，毕竟数学建模不是数据挖掘类型的比赛。

除非你使用这个机器学习的模型带来的结果准确率的提升非常大

如果大家真的要在数学建模论文中使用机器学习的模型的话，我推荐使用集成算法的模型，特别是使用随机森林。在写数模论文的时候，你要交代为什么你要用这个模型，

原因可以从下面几点考虑：（不要让别人看出来你是在乱套模型！）

（1）在我研究的这个问题中，有别的学者也用过随机森林来进行预测，效果还很好，可以在论文中列出相应的参考论文；

（2） 随机森林是集成学习算法，它通常比个体学习器表现的效果更好，因此你可以找一些基础的模型和他进行对比，例如线性判别分析、逻辑回归、knn 等；

（3） 随机森林可以给我们估计输入指标的重要性，可以帮助我们进行进行特征选择筛选出无关的特征，有些题目就需要我们做这样的事情。

意思就是，随机森林在用出来效果比较好的时候，和比如选影响更大的指标的时候，是可以用的。

从上面三点进行阐述

标签 AT, Matlab, 学习

MATLAB初步进行机器学习