文章目录
- 一、概述
-
- (一)二次规划标准形式
- (二)输入参数
- (三)输出参数
- 二、MATLAB基础语法
- 三、MATLAB典型求解样例
-
- (一)具有线性不等式约束的二次规划
- (二)具有线性等式约束的二次规划
- (三)具有线性约束和边界的二次规划
一、概述
二次规划是指约束为线性的二次优化问题。在Matlab中,quadprog是具有线性约束的二次目标函数求解器。
(一)二次规划标准形式
min
x
1
2
x
T
H
x
+
f
T
x
\mathop {\min }\limits_x \frac{1}{2}{{\bf{x}}^{\bf{T}}}{\bf{Hx}} + {{\bf{f}}^{\bf{T}}}{\bf{x}}
xmin21xTHx+fTx
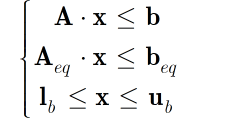 其实H是Hessian 阵,是n乘n的对称阵。
其实H是Hessian 阵,是n乘n的对称阵。
1、海森矩阵的正定性与函数最优性
- 如果 Hessian 矩阵是半正定的,则我们说该式是一个凸二次规划,在这种情况下该问题的困难程度类似于线性规划。如果有至少一个向量满足约束并且在 可行域 有下界,则凸二次规划问题就有一个全局最小值。
- 如果是正定的,则这类二次规划为严格的凸二次规划,那么全局最小值就是唯一的。
- 如果是一个 不定矩阵 ,则为非凸二次规划,这类二次规划更有挑战性,因为它们有多个平稳点和局部极小值点。
2、基本数学概念
- 基础概念:https://blog.csdn.net/jbb0523/article/details/50598523
- 凸 严格凸,举例:https://zhuanlan.zhihu.com/p/399549564
3、对称阵的正定性判断
- 正定矩阵:矩阵的所有特征值均大于0
- 半正定矩阵:矩阵的所有特征值均非负
- 负定矩阵:矩阵所有特征值均小于0
https://blog.csdn.net/Infinity_07/article/details/109569450

4、matlab正、半正、负定阵生成,与quadprog验证
(1)matlab判断正定性:
% 判断矩阵m是正定、半正定还是负定
m = [2 -1; -1 2];
if issymmetric(m) % 检查矩阵是否对称
% disp('矩阵对称');
d = eig(m); % 计算矩阵特征值
if all(d > 0)
disp('矩阵正定');
elseif all(d >= 0)
disp('矩阵半正定');
else
disp('矩阵负定');
end
else
disp('矩阵不对称');
end
(2)matlab产生正定阵的操作
https://blog.csdn.net/zhao523520704/article/details/52918376/
H_posi=diag([1,2,3]);
H_semi=diag([0,2,3]);
H_nega=diag([-1,-2,-3]);
(二)输入参数
| 符号 | 参数含义 |
|---|---|
| H | 二次目标矩阵 |
| f | 线性目标向量 |
| A | 线性不等式矩阵 |
| b | 线性不等式向量 |
| Aeq | 线性等式约束矩阵 |
| beq | 线性等式约束向量 |
| lb | 下界 |
| ub | 上界 |
(三)输出参数
| 符号 | 参数含义 |
|---|---|
| x | 解,以实数向量形式返回 |
| wsout | 解的热启动对象 |
| fval | 再解处的目标函数值 |
| exitflag | quadprog停止的原因 |
| output | 有关优化过程的信息,以结构体形式返回 |
| lambda | 解处的拉格朗日乘数 |
二、MATLAB基础语法
x = quadprog(H,f)
x = quadprog(H,f,A,b)
x = quadprog(H,f,A,b,Aeq,beq)
x = quadprog(H,f,A,b,Aeq,beq,lb,ub)
x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0)
x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options)
x = quadprog(problem)
[x,fval] = quadprog(___)
[x,fval,exitflag,output] = quadprog(___)
[x,fval,exitflag,output,lambda] = quadprog(___)
[wsout,fval,exitflag,output,lambda] = quadprog(H,f,A,b,Aeq,beq,lb,ub,ws)
三、MATLAB典型求解样例
(一)具有线性不等式约束的二次规划

H = [1 -1; -1 2];
f = [-2; -6];
A = [1 1; -1 2; 2 1];
b = [2; 2; 3];
[x,fval,exitflag,output,lambda] = quadprog(H,f,A,b);
x =
0.6667
1.3333
fval = -8.2222
exitflag =
1
(二)具有线性等式约束的二次规划

H = [1 -1; -1 2];
f = [-2; -6];
Aeq = [1 1];
beq = 0;
[x,fval,exitflag,output,lambda] = ...
quadprog(H,f,[],[],Aeq,beq)
x = -0.8000
0.8000
fval = -1.6000
exitflag =
1
(三)具有线性约束和边界的二次规划
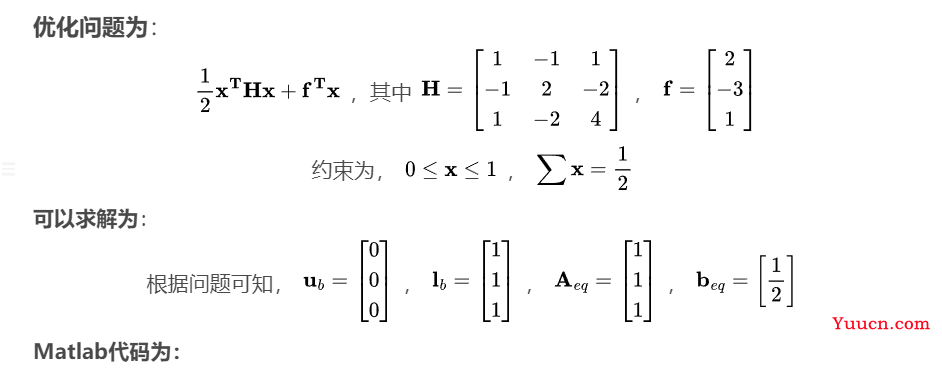
H = [1,-1,1
-1,2,-2
1,-2,4];
f = [2;-3;1];
lb = zeros(3,1);
ub = ones(size(lb));
Aeq = ones(1,3);
beq = 1/2;
x = quadprog(H,f,[],[],Aeq,beq,lb,ub);