文章目录
- 参考资料
- 1. 基本模型建立
-
- 平动
- 转动
- 2. 横向(y方向)受力计算
- 3. 横向动力学模型推导
-
- 补充——考虑路面坡度角
- 4. 纵向(x方向)受力计算
- 5. 动力学模型总结
参考资料
- 车辆数学模型
- 车辆模型-动力学模型(Dynamics Model)
1. 基本模型建立
我们作如下假设:
- 车辆所受的空气的力只会对车身坐标系x轴方向上的运动有影响,y轴方向和沿着z轴的旋转不会受到空气力的影响;
- 车辆运行在二维平面中,也就是z轴无速度。
- 车辆轮胎力运行在线性区间。
在运动学模型中,我们假设了单车模型中前后轮的速度矢量与轮子方向一致。当车辆速度很高时,单车模型中前后轮的速度矢量不再与轮子方向一致。此时运动学模型就不能准确地描述车辆的运动状态,这就需要使用动力学模型对车辆进行建模。
车辆单车模型中需要考虑两个维度的信息,这两个维度分别指代表车辆横向位置信息的
y
y
y和表示车辆偏航角信息的
ψ
\psi
ψ。他们可以大致分为两类: 纵向力(Longitudinal force) 和 横向力(Lateral force), 纵向力就是使车辆前后移动的力量,而横向力则促使车辆在横向移动,在力的相互作用过程中,轮胎起着决定性的作用(根据一定的物理常识,轮胎是车辆运动的一个重要的力的来源)。
之所以叫二自由度的车辆动力学模型,就是因为二自由度指的是横向上y轴的运动和绕z轴的转动,忽略了纵向x轴的运动。
建立如下坐标系,X,Y表示全局坐标系,x,y则表示车身坐标系,x轴方向沿车辆中轴方向向前,y轴方向朝右,其车辆中心在质心位置。车辆的状态信息表示为
(
x
,
y
,
ψ
,
v
)
(x,y,\psi,v)
(x,y,ψ,v),即
x
,
y
x,y
x,y方向上的位置,偏航角和速度。
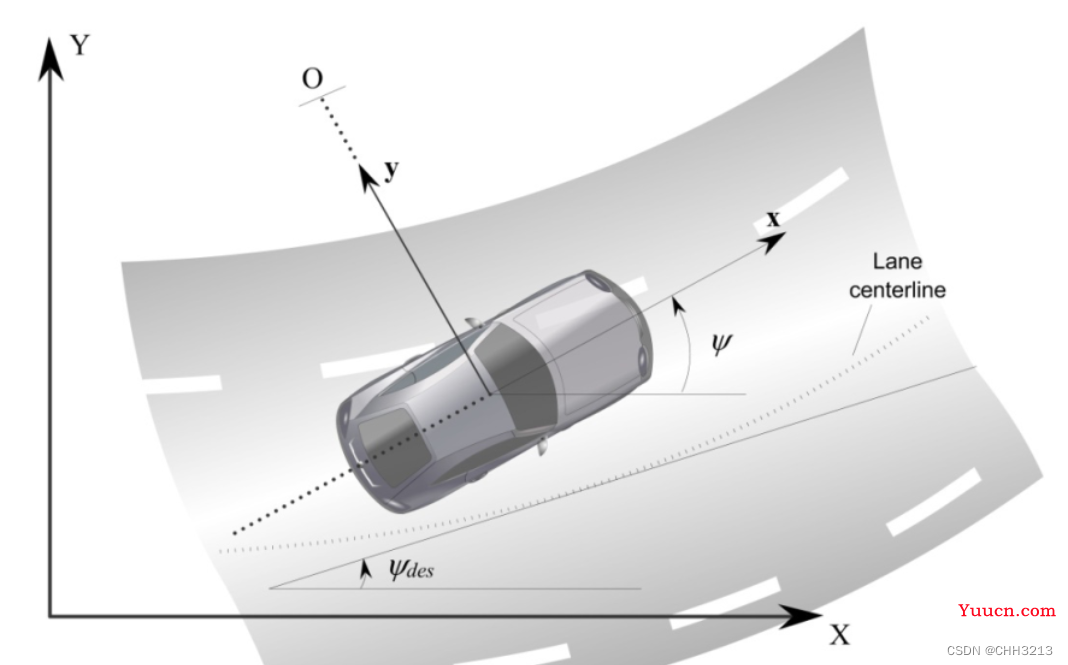
平动
首先假设车辆为一个质点,对该质点进行受力分析,并根据牛顿第二定律得
m
a
y
=
F
y
f
+
F
y
r
m
a
x
=
F
x
f
+
F
x
r
−
F
a
e
r
o
(1)
\tag{1} m a_{y}=F_{y f}+F_{y r}\\ ma_x=F_{xf}+F_{xr}-F_{aero}
may=Fyf+Fyrmax=Fxf+Fxr−Faero(1)
其中,
-
a
y
a_{y}
ay 为车辆重心处
y
y
y 轴方向的惯性加速度,满足
a
y
=
d
2
y
d
t
2
a_y=\frac{d^2y}{dt^2}
ay=dt2d2y -
F
y
f
F_{y f}
Fyf 和
F
y
r
F_{y r}
Fyr 分别表示车前轮和后轮所受到的力在y轴方向上的分量。 -
F
x
f
F_{x f}
Fxf 和
F
x
r
F_{x r}
Fxr分别表示车前轮和后轮所受到的力在x轴方向上的分量。 -
F
a
e
r
o
F_{aero}
Faero表示车在x轴方向受到的空气阻力。
平动过程中,有两 种力共同作用产生加速度
a
y
a_{y}
ay : 车辆延
y
y
y 轴产生的惯性加速度
y
¨
\ddot{y}
y¨ 和车辆绕旋转中心
O
O
O 旋转产生的向心加速度
a
c
=
v
x
2
R
=
v
x
ψ
˙
∘
a_{c}=\frac{{v_x}^2}{R}=v_{x} \dot{\psi}_{\circ}
ac=Rvx2=vxψ˙∘
a
y
=
y
¨
+
v
x
ψ
˙
(2)
\tag{2} a_{y}=\ddot{y}+v_{x} \dot{\psi}
ay=y¨+vxψ˙(2)
将公式(2)带入公式(1)得
m
(
y
¨
+
v
x
ψ
˙
)
=
F
y
f
+
F
y
r
(3)
\tag{3} m\left(\ddot{y}+v_{x} \dot{\psi}\right)=F_{y f}+F_{y r}
m(y¨+vxψ˙)=Fyf+Fyr(3)
同理,沿着x轴有
a
x
=
v
˙
x
−
v
y
ψ
˙
m
(
v
˙
x
−
v
y
ψ
˙
)
=
F
x
f
+
F
x
r
−
F
a
e
r
o
(3-2)
\tag{3-2} a_x=\dot{v}_x-v_y\dot{\psi}\\ m(\dot{v}_x-v_y\dot{\psi})=F_{xf}+F_{xr}-F_{aero}
ax=v˙x−vyψ˙m(v˙x−vyψ˙)=Fxf+Fxr−Faero(3-2)
其中,
v
x
˙
=
x
¨
v
y
˙
=
y
¨
\dot{v_x}=\ddot{x}\\ \dot{v_y}=\ddot{y}
vx˙=x¨vy˙=y¨
转动
假设车辆为刚体,刚体绕重心转动,该运动过程使用力矩和转动惯量进行描述。 车辆绕Z轴旋转产生的力矩平衡,对应的偏航动力学方程为
I
z
ψ
¨
=
l
f
F
y
f
−
l
r
F
y
r
(4)
\tag{4} I_{z} \ddot{\psi}=l_{f} F_{y f}-l_{r} F_{y r}
Izψ¨=lfFyf−lrFyr(4)
其中,
l
f
l_{f}
lf 和
l
r
l_{r}
lr 代表前后轮胎到重心的距离。
2. 横向(y方向)受力计算
车辆轮胎在y轴方向受到的力
F
y
f
F_{yf}
Fyf、
F
y
r
F_{yr}
Fyr实验结果表明,其大小正比于轮胎的侧滑角。其侧滑角如下图所示:
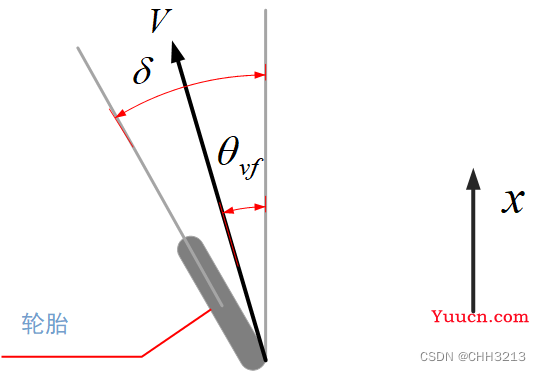
根据上图,前轮侧滑角为
α
f
=
δ
−
θ
v
f
(5)
\tag{5} \alpha_{f}=\delta-\theta_{v f}
αf=δ−θvf(5)
其中,
θ
v
f
\theta_{v f}
θvf 代表速度矢量与车辆纵轴的夹角,
δ
\delta
δ 代表前轮转向角。
同理,由于后轮转向角
δ
\delta
δ 为 0 ,故后轮侧滑角为
α
r
=
−
θ
v
r
(6)
\tag{6} \alpha_{r}=-\theta_{vr}
αr=−θvr(6)
车辆前轮的横向力可以表示为
F
y
f
=
2
C
α
f
(
δ
−
θ
v
f
)
(7)
\tag{7} F_{y f}=2 C_{\alpha f}\left(\delta-\theta_{v f}\right)
Fyf=2Cαf(δ−θvf)(7)
其中,比例常数
C
α
f
C_{\alpha f}
Cαf 代表每个前轮的转弯刚度(cornering stiffness)。
同理后轮的横向力可以写为
F
y
r
=
2
C
α
r
(
−
θ
v
r
)
(8)
\tag{8} F_{y r}=2 C_{\alpha r}\left(-\theta_{v r}\right)
Fyr=2Cαr(−θvr)(8)
其中,比例常数
C
α
r
C_{\alpha r}
Cαr 代表每个后轮的转弯刚度(cornering stiffness)。
3. 横向动力学模型推导
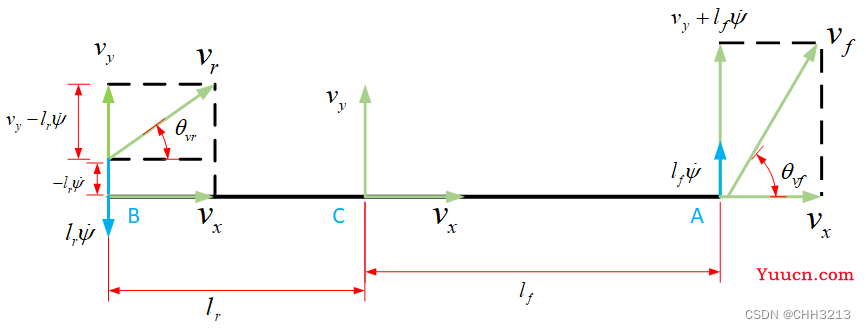
点 C 代表车辆的重心, A 点和 B点到重心的距离分别用
l
f
l_f
lf和
l
r
l_r
lr表示,轴距表示为
L
=
l
f
+
l
r
L = l_f + l_r
L=lf+lr。
车辆平动产生的速度分量
v
x
v_{x}
vx 和
v
y
v_{y}
vy ,以及绕点
C
C
C 转动产生的线速度
l
f
ψ
˙
l_{f} \dot{\psi}
lfψ˙ 和
l
r
ψ
˙
l_{r} \dot{\psi}
lrψ˙ (根据角速度与线速度的关系
ω
=
v
R
\omega=\frac{v}{R}
ω=Rv得到)组成。根据上图得
tan
(
θ
v
f
)
=
v
y
+
l
f
ψ
˙
v
x
(9)
\tag{9} \tan \left(\theta_{v f}\right)=\frac{v_{y}+l_{f} \dot{\psi}}{v_{x}}
tan(θvf)=vxvy+lfψ˙(9)
tan
(
θ
v
r
)
=
v
y
−
l
r
ψ
˙
v
x
(10)
\tag{10} \tan \left(\theta_{v r}\right)=\frac{v_{y}-l_{r} \dot{\psi}}{v_{x}}
tan(θvr)=vxvy−lrψ˙(10)
由于通常情况下速度矢量的夹角很小,可以使用小角度近似原理
tan
(
δ
)
≈
δ
\tan \left(\delta\right) \approx \delta
tan(δ)≈δ
得
θ
v
f
=
y
˙
+
l
f
ψ
˙
v
x
(11)
\tag{11} \theta_{v f}=\frac{\dot{y}+l_{f} \dot{\psi}}{v_{x}}
θvf=vxy˙+lfψ˙(11)
θ
v
r
=
y
˙
−
l
r
ψ
˙
v
x
(12)
\tag{12} \theta_{v r}=\frac{\dot{y}-l_{r} \dot{\psi}}{v_{x}}
θvr=vxy˙−lrψ˙(12)
将等式(7)、(8)、(11)和(12)代入等式(3)中得
m
(
y
¨
+
v
x
ψ
˙
)
=
2
C
α
f
(
δ
−
y
˙
+
l
f
ψ
˙
v
x
)
+
2
C
α
r
(
−
y
˙
−
l
r
ψ
˙
v
x
)
(13)
\tag{13} m\left(\ddot{y}+v_{x} \dot{\psi}\right)=2 C_{\alpha f}\left(\delta-\frac{\dot{y}+l_{f} \dot{\psi}}{v_{x}}\right)+2 C_{\alpha r}\left(-\frac{\dot{y}-l_{r} \dot{\psi}}{v_{x}}\right)
m(y¨+vxψ˙)=2Cαf(δ−vxy˙+lfψ˙)+2Cαr(−vxy˙−lrψ˙)(13)
等式(13)左右两边同时除以
m
m
m ,分别提取
y
¨
、
y
˙
、
ψ
˙
\ddot{y} 、 \dot{y} 、 \dot{\psi}
y¨、y˙、ψ˙ 和
δ
\delta
δ 项得
y
¨
=
−
2
C
α
f
+
2
C
α
r
m
v
x
y
˙
−
(
v
x
+
2
C
α
f
l
f
−
2
C
α
r
l
r
m
v
x
)
ψ
˙
+
2
C
α
f
m
δ
(14)
\tag{14} \ddot{y}=-\frac{2 C_{\alpha f}+2 C_{\alpha r}}{m v_{x}} \dot{y}-\left(v_{x}+\frac{2 C_{\alpha f} l_{f}-2 C_{\alpha r} l_{r}}{m v_{x}}\right) \dot{\psi}+\frac{2 C_{\alpha f}}{m} \delta
y¨=−mvx2Cαf+2Cαry˙−(vx+mvx2Cαflf−2Cαrlr)ψ˙+m2Cαfδ(14)
转化为矩阵形式如下
y
¨
=
[
−
2
C
α
f
+
2
C
α
r
m
V
x
−
(
v
x
+
2
C
α
f
l
f
−
2
C
α
r
l
r
m
v
x
)
]
[
y
y
˙
ψ
ψ
˙
]
+
2
C
α
f
m
δ
(15)
\tag{15} \ddot{y}=\left[\begin{array}{llll} 0 & -\frac{2 C_{\alpha f}+2 C_{\alpha r}}{m V_{x}} & 0 & -\left(v_{x}+\frac{2 C_{\alpha f} l_{f}-2 C_{\alpha r} l_{r}}{m v_{x}}\right) \end{array}\right]\left[\begin{array}{l} y \\ \dot{y} \\ \psi \\ \dot{\psi} \end{array}\right]+\frac{2 C_{\alpha f}}{m} \delta
y¨=[0−mVx2Cαf+2Cαr0−(vx+mvx2Cαflf−2Cαrlr)]⎣⎡yy˙ψψ˙⎦⎤+m2Cαfδ(15)
同理,将等式(7)、(8)、(11)和(12)代入等式(4)中得
I
z
ψ
¨
=
2
l
f
C
α
f
(
δ
−
y
˙
+
l
f
ψ
˙
v
x
)
−
2
l
r
C
α
r
(
−
y
˙
−
l
r
ψ
˙
v
x
)
(16)
\tag{16} I_{z} \ddot{\psi}=2 l_{f} C_{\alpha f}\left(\delta-\frac{\dot{y}+l_{f} \dot{\psi}}{v_{x}}\right)-2 l_{r} C_{\alpha r}\left(-\frac{\dot{y}-l_{r} \dot{\psi}}{v_{x}}\right)
Izψ¨=2lfCαf(δ−vxy˙+lfψ˙)−2lrCαr(−vxy˙−lrψ˙)(16)
等式(16)左右两边同时除以
I
z
I_{z}
Iz ,分别提取
y
˙
、
ψ
¨
、
ψ
˙
\dot{y} 、 \ddot{\psi} 、 \dot{\psi}
y˙、ψ¨、ψ˙ 和
δ
\delta
δ 项得
ψ
¨
=
−
2
l
f
C
α
f
−
2
l
r
C
α
r
I
z
v
x
y
˙
−
2
l
f
2
C
α
f
+
2
l
r
2
C
α
r
I
z
v
x
ψ
˙
+
2
l
f
C
α
f
I
z
δ
(17)
\tag{17} \ddot{\psi}=-\frac{2 l_{f} C_{\alpha f}-2 l_{r} C_{\alpha r}}{I_{z} v_{x}} \dot{y}-\frac{2 l_{f}{ }^{2} C_{\alpha f}+2 l_{r}{ }^{2} C_{\alpha r}}{I_{z} v_{x}} \dot{\psi}+\frac{2 l_{f} C_{\alpha f}}{I_{z}} \delta
ψ¨=−Izvx2lfCαf−2lrCαry˙−Izvx2lf2Cαf+2lr2Cαrψ˙+Iz2lfCαfδ(17)
等效的矩阵形式为
ψ
¨
=
[
−
2
l
f
C
α
f
−
2
l
r
C
α
r
I
z
v
x
−
2
l
f
2
C
α
f
+
2
l
r
2
C
α
r
I
z
v
x
]
[
y
y
˙
ψ
ψ
˙
]
+
2
l
f
C
α
f
I
z
δ
(18)
\tag{18} \ddot{\psi}=\left[\begin{array}{llll} 0 & -\frac{2 l_{f} C_{\alpha f}-2 l_{r} C_{\alpha r}}{I_{z} v_{x}} & 0 & -\frac{2 l_{f}{ }^{2} C_{\alpha f}+2 l_{r}{ }^{2} C_{\alpha r}}{I_{z} v_{x}} \end{array}\right]\left[\begin{array}{l} y \\ \dot{y} \\ \psi \\ \dot{\psi} \end{array}\right]+\frac{2 l_{f} C_{\alpha f}}{I_{z}} \delta
ψ¨=[0−Izvx2lfCαf−2lrCαr0−Izvx2lf2Cαf+2lr2Cαr]⎣⎡yy˙ψψ˙⎦⎤+Iz2lfCαfδ(18)
根据等式(15)和(18)得
[
y
˙
y
¨
ψ
˙
ψ
¨
]
=
[
1
−
2
C
α
f
+
2
C
α
r
m
V
x
−
(
V
x
+
2
C
α
f
l
f
−
2
C
α
r
l
r
m
V
x
)
1
−
2
l
f
C
α
f
−
2
l
r
C
α
r
I
z
V
x
−
2
l
f
2
C
α
f
+
2
l
r
2
C
α
r
I
z
V
x
]
[
y
y
˙
ψ
ψ
˙
]
+
[
2
C
α
f
m
2
l
f
C
α
f
I
z
]
δ
(19)
\tag{19} \begin{aligned} \left[\begin{array}{c} \dot{y} \\ \ddot{y} \\ \dot{\psi} \\ \ddot{\psi} \end{array}\right]=\left[\begin{array}{cccc} 0 & 1 & 0 & 0 \\ 0 & -\frac{2 C_{\alpha f}+2 C_{\alpha r}}{m V_{x}} & 0 & -\left(V_{x}+\frac{2 C_{\alpha f} l_{f}-2 C_{\alpha r} l_{r}}{m V_{x}}\right) \\ 0 & 0 & 0 & 1 \\ 0 & -\frac{2 l_{f} C_{\alpha f}-2 l_{r} C_{\alpha r}}{I_{z} V_{x}} & 0 & -\frac{2 l_{f}{ }^{2} C_{\alpha f}+2 l_{r}{ }^{2} C_{\alpha r}}{I_{z} V_{x}} \end{array}\right]\left[\begin{array}{c} y \\ \dot{y} \\ \psi \\ \dot{\psi} \end{array}\right] \\ +\left[\begin{array}{c} 0\\ \frac{2 C_{\alpha f}}{m} \\ 0 \\ \frac{2 l_{f} C_{\alpha f}}{I_{z}} \end{array}\right] \delta \end{aligned}
⎣⎡y˙y¨ψ˙ψ¨⎦⎤=⎣⎡00001−mVx2Cαf+2Cαr0−IzVx2lfCαf−2lrCαr00000−(Vx+mVx2Cαflf−2Cαrlr)1−IzVx2lf2Cαf+2lr2Cαr⎦⎤⎣⎡yy˙ψψ˙⎦⎤+⎣⎡0m2Cαf0Iz2lfCαf⎦⎤δ(19)
注意:上述动力学方程的推导建立在车辆侧滑角很小的情况下,这时的轮胎作用力与侧滑角可以近似为线性关系。当侧滑角很大时,轮胎作用力与侧滑角就不再是线性关系。
补充——考虑路面坡度角
如果还额外考虑路面坡度角(road bank angles)的影响,则公式(1)应写为
m
a
y
=
F
y
f
+
F
y
r
+
F
b
a
n
k
m a_{y}=F_{y f}+F_{y r}+F_{bank}
may=Fyf+Fyr+Fbank
式中
F
b
a
n
k
=
m
g
sin
ϕ
F_{bank} = mg\sin{\phi}
Fbank=mgsinϕ
ϕ
\phi
ϕ为路面坡度角,如下图所示
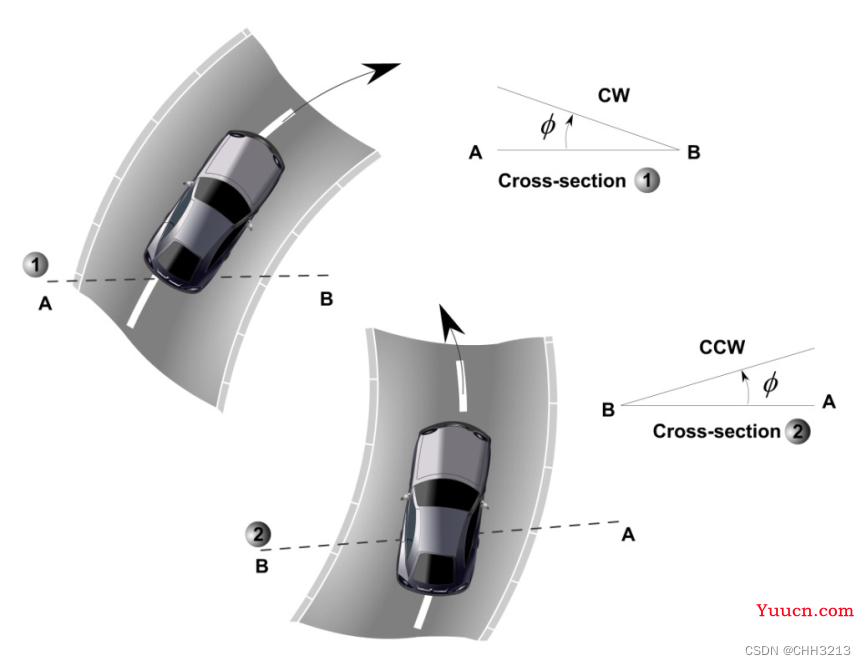
转动过程不受坡度角影响,即公式(4)不变。因此,其它按部就班推导即可。
4. 纵向(x方向)受力计算
车辆在
x
\mathrm{x}
x 轴方向的力
F
x
f
、
F
x
r
F_{x f} 、 F_{x r}
Fxf、Fxr 与轮胎的滑比
σ
x
\sigma_{x}
σx 成正比。其定义为:
{
σ
x
=
r
e
f
f
ω
w
−
v
x
v
x
——刹车时
σ
x
=
r
e
f
f
ω
w
−
v
x
r
e
f
f
ω
w
——加速时
(20)
\tag{20} \left\{\begin{array}{l} \sigma_{x}=\frac{r_{e f f} \omega_{w}-v_{x}}{v_{x}} \text { ——刹车时 } \\ \sigma_{x}=\frac{r_{e f f} \omega_{w}-v_{x}}{r_{e f f} \omega_{w}} \text { ——加速时 } \end{array}\right.
{σx=vxreffωw−vx ——刹车时 σx=reffωwreffωw−vx ——加速时 (20)
因此有:
F
x
f
=
2
C
σ
f
σ
x
f
(21)
\tag{21} F_{x f}=2 C_{\sigma f} \sigma_{x f}
Fxf=2Cσfσxf(21)
F
x
r
=
2
C
σ
r
σ
x
r
(22)
\tag{22} F_{x r}=2 C_{\sigma r} \sigma_{x r}
Fxr=2Cσrσxr(22)
其中
C
σ
r
C_{\sigma r}
Cσr 为纵向的轮胎刚性参数(tire stiffness parameters)。
对于空气阻力 :
F
aero
=
1
2
ρ
C
d
A
F
(
v
x
+
v
wind
)
2
(23)
\tag{23} F_{\text {aero }}=\frac{1}{2} \rho C_{d} A_{F}\left(v_{x}+v_{\text {wind }}\right)^{2}
Faero =21ρCdAF(vx+vwind )2(23)
另外在全局坐标系下:
{
X
˙
=
v
x
cos
(
ψ
)
−
v
y
sin
(
ψ
)
Y
˙
=
v
x
sin
(
ψ
)
+
v
y
cos
(
ψ
)
(24)
\tag{24} \left\{\begin{array}{l} \dot{X}=v_{x} \cos (\psi)-v_{y} \sin (\psi) \\ \dot{Y}=v_{x} \sin (\psi)+v_{y} \cos (\psi) \end{array}\right.
{X˙=vxcos(ψ)−vysin(ψ)Y˙=vxsin(ψ)+vycos(ψ)(24)
联立等式(3-2),(21),(22),(23),得
v
˙
x
=
2
C
σ
r
σ
x
r
+
2
C
σ
f
σ
x
f
−
1
2
ρ
C
d
A
F
(
v
x
+
v
w
i
n
d
)
2
m
+
v
y
ψ
˙
(25)
\tag{25} \dot{v}_{x}=\frac{2 C_{\sigma r} \sigma_{x r}+2 C_{\sigma f} \sigma_{x f}-\frac{1}{2} \rho C_{d} A_{F}\left(v_{x}+v_{w i n d}\right)^{2}}{m}+v_{y} {\dot{\psi}}
v˙x=m2Cσrσxr+2Cσfσxf−21ρCdAF(vx+vwind)2+vyψ˙(25)
5. 动力学模型总结
联立等式(14),(17),(24),(25)得
{
X
˙
=
v
x
cos
(
ψ
)
−
v
y
sin
(
ψ
)
Y
˙
=
v
x
sin
(
ψ
)
+
v
y
cos
(
ψ
)
x
˙
=
v
x
y
˙
=
v
y
v
˙
x
=
2
C
σ
r
σ
x
r
+
2
C
σ
f
σ
x
f
−
1
2
ρ
C
d
A
F
(
v
x
+
v
w
i
n
d
)
2
m
+
v
y
ψ
˙
v
˙
y
=
−
2
C
α
f
+
2
C
α
r
m
v
x
y
˙
−
(
v
x
+
2
C
α
f
l
f
−
2
C
α
r
l
r
m
v
x
)
ψ
˙
+
2
C
α
f
m
δ
ψ
¨
=
−
2
l
f
C
α
f
−
2
l
r
C
α
r
I
z
v
x
y
˙
−
2
l
f
2
C
α
f
+
2
l
r
2
C
α
r
I
z
v
x
ψ
˙
+
2
l
f
C
α
f
I
z
δ
(26)
\tag{26} \left\{\begin{array}{l} \dot{X}=v_{x} \cos (\psi)-v_{y} \sin (\psi) \\ \dot{Y}=v_{x} \sin (\psi)+v_{y} \cos (\psi)\\ \dot{x}=v_x\\ \dot{y}=v_y\\ \dot{v}_{x}=\frac{2 C_{\sigma r} \sigma_{x r}+2 C_{\sigma f} \sigma_{x f}-\frac{1}{2} \rho C_{d} A_{F}\left(v_{x}+v_{w i n d}\right)^{2}}{m}+v_{y} {\dot{\psi}}\\ \dot{v}_y=-\frac{2 C_{\alpha f}+2 C_{\alpha r}}{m v_{x}} \dot{y}-\left(v_{x}+\frac{2 C_{\alpha f} l_{f}-2 C_{\alpha r} l_{r}}{m v_{x}}\right) \dot{\psi}+\frac{2 C_{\alpha f}}{m} \delta\\ \ddot{\psi}=-\frac{2 l_{f} C_{\alpha f}-2 l_{r} C_{\alpha r}}{I_{z} v_{x}} \dot{y}-\frac{2 l_{f}{ }^{2} C_{\alpha f}+2 l_{r}{ }^{2} C_{\alpha r}}{I_{z} v_{x}} \dot{\psi}+\frac{2 l_{f} C_{\alpha f}}{I_{z}} \delta \end{array}\right.
⎩⎨⎧X˙=vxcos(ψ)−vysin(ψ)Y˙=vxsin(ψ)+vycos(ψ)x˙=vxy˙=vyv˙x=m2Cσrσxr+2Cσfσxf−21ρCdAF(vx+vwind)2+vyψ˙v˙y=−mvx2Cαf+2Cαry˙−(vx+mvx2Cαflf−2Cαrlr)ψ˙+m2Cαfδψ¨=−Izvx2lfCαf−2lrCαry˙−Izvx2lf2Cαf+2lr2Cαrψ˙+Iz2lfCαfδ(26)