1. 题目

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

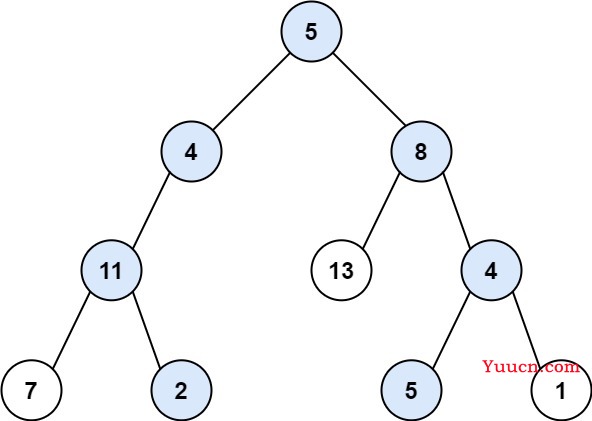
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

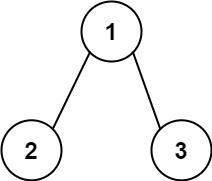
输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：
输入：root = [1,2], targetSum = 0
输出：[]

提示：

树中节点总数在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/5dy6pt/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

2. 解题思路

首先能够想到的是用二叉树递归的方式来查找路径，每次递归都需要修改target的值，在这种做法中有一个问题：如何设置返回值，从而返回路径列表，且在程序中如何修改路径列表？

在官方题解中，在类的定义中适用result、path两个公共变量，可以让不同的函数均基于这块公共区域加以修改。

遍历使用的是先序遍历。

• 如果需要继续遍历，将当前结点放入path路径中；
• 如果已经遍历到叶子结点，且路径之和等于target的值，将当前的路径整体放入结果列表中；
• 当某一层遍历结束之后，需要将当前结点弹出路径列表中，实现二叉遍历

需要注意的是，由于list.add()使用的是浅拷贝，如果每次将path添加到结果列表中使用的是result.add(path)，这样写忽略了list.add()是进行浅拷贝的，即每个路径结果path都指向同一个内存地址，后续在此内存地址上的操作将会改变前期的结果。最终出现[[x,y,z][x,y,z][x,y,z]]三个子列表相同的情况。因此，每次写入result列表应该新建一个path对象。

3. 数据类型功能函数总结

//LinkedList
LinkedList<E> listname=new LinkedList<E>();//初始化
LinkedList<E> listname=new LinkedList<E>(oldlist);//将oldlist的元素复制一份给listname，且是深拷贝
LinkedList.add(elment);//在链表尾部添加元素
LinkedList.removeFirst();//取出链表头部元素

4. java代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
 // 考虑迭代，左右子树再找某个目标值的路径。
class Solution {
    LinkedList<List<Integer>> result=new LinkedList<List<Integer>>();
    LinkedList<Integer> path=new LinkedList<Integer>();
    public List<List<Integer>> pathSum(TreeNode root, int target) {
        recur(root,target);
        return result;
    }
    void recur(TreeNode root, int target) {
        if(root!=null){
            path.add(root.val);
            target-=root.val;
            if(target==0&&root.left==null&&root.right==null){//遍历到叶节点且目标值正好等于路径之和
                LinkedList<Integer> path_temp=new LinkedList<Integer>(path);
                result.add(path_temp);
            }
            recur(root.left,target);
            recur(root.right,target);
            path.removeLast();//回退时将当前元素出栈
        }
    }
}