树状数组介绍
树状数组,顾名思义,就是树状的一维数组。
二叉树同样也可以用一维数组存储。我们以二叉树进行类比。
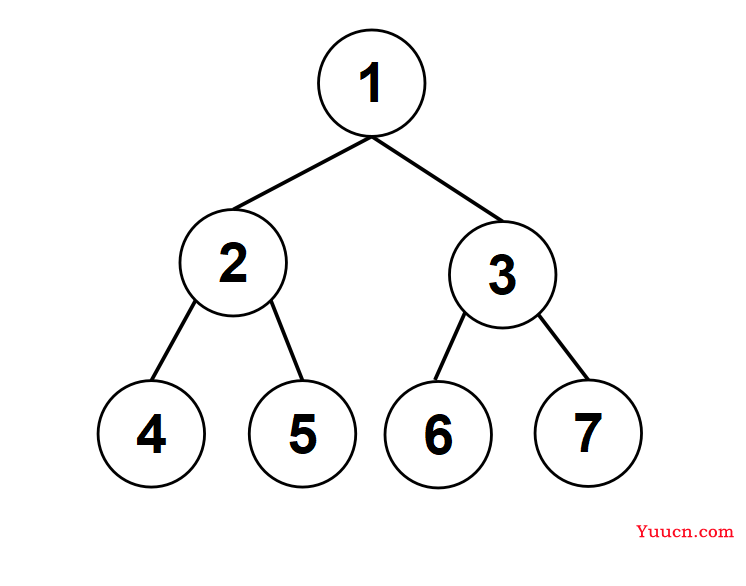
如图所示,图中节点的序号就是存在数组中的下标。
记父节点序号为 \(p\),子节点序号为 \(s\)。
则有:
\(p\) \(=\) \(s\) \(/\) \(2\) (向下取整)。
左子节点 \(s_{left}\) \(=\) \(p\) \(* 2\) 。
右子节点 \(s_{right}\) \(=\) \(p\) \(*2+1\) 。
综上可知,二叉树能用一维数组存,是由于其父子节点间存在一定关系,以至于不需要用额外的变量来表示信息。
那类比到树状数组中,可以发现:
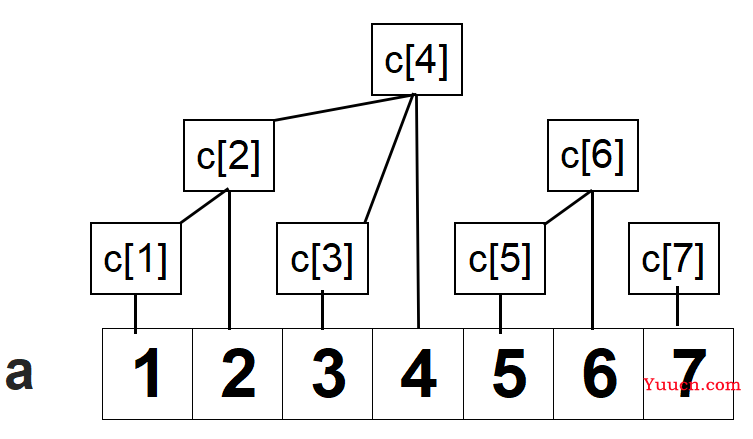
\(c\)数组即为树状数组。\(c_i\) 表示区间\(a\)\([i-lowbit(i),i]\) 的和。
ps:点我了解lowbit运算是什么
同样记父节点下标为 \(p\) ,子节点下标为 \(s\)。
则有:
\(p\) \(=\) \(s\) \(+\) \(lowbit(s)\)。
由这条公式亦可反推出:
\(s\) \(=\) \(p\) \(-\) \(2^i\)(\(0 \le i < p_{last}\))
这里的 \(p_{last}\) 指的是 \(p\) 二进制表示下最后一位 \(1\) 所在的位数。
例如:\(6\) 的二进制数表示为 \(110\),则它的 \(p_{last}\) 为 \(1\)。(这里的位数从右往左从\(0\)开始记)。
因为公式 \(1\) 由 \(s\) 加上自身 \(lowbit(s)\) 得到 \(p\) 其过程一定会产生进位。且 \(lowbit(s)\) 一定小于 \(lowbit(p)\) ,所以可以倒推得到子节点。
由于以上关系,树状数组不仅可以用一维数组存。而且还衍生出了一系列用途。
树状数组功能
单点增加
Q:给序列中的一个数 \(a[x]\) 加上 \(y\) 。此时如何维护树状数组?
A:将所有包含 \(a[x]\) 的节点加上 \(y\) 即可,也就是 \(c[x]\) 和它所有的祖先节点。
ps:初始化时亦可运用此操作。
点击查看代码
void add(int x,int y){
for (; x <= N;x += x&-x) c[x] += y;
return ;
}
动态维护前缀和
之所以说动态维护,因为用树状数组维护前缀和只需要 \(\log N\) 的时间复杂度。更为优秀。
Q:求 \(a\) 数组 \(a_i \sim a_x\) 的和。
A:将数 \(x\) 分成若干个区间。
区间共同特点:若区间结尾为 \(R\),则区间长度就等于 \(lowbit(R)\),即 \(R\) 二进制分解下最小的整数次幂。
举例:当 \(x\) = \(7\) 时
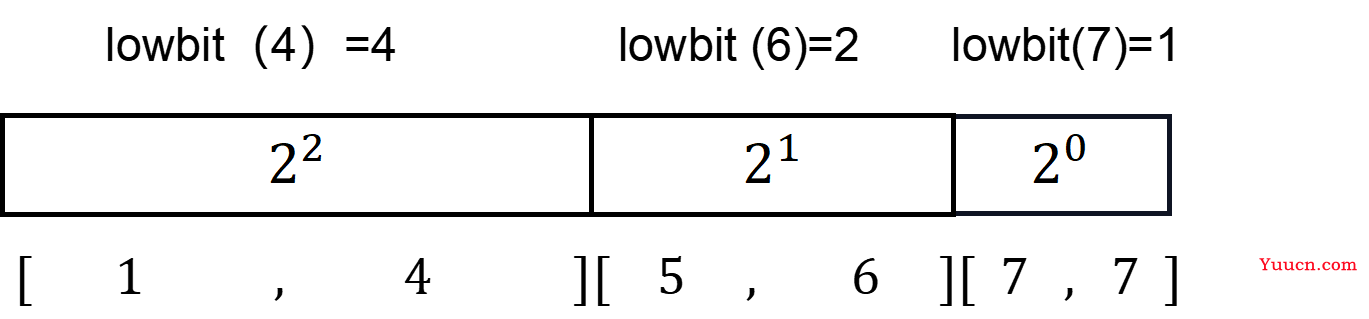
如图所示。
区间划分方式与树状数组相同。前面又提到“\(c\)数组即为树状数组。\(c_i\) 表示区间\(a\)\([i-lowbit(i),i]\) 的和。”
因此只需要将这几个区间所对应的 \(c_i\) 相加。即可得到前缀和。
点击查看代码
int ask(int x){
int ans = 0;
for (; x ; x -= x & -x) ans += c[x];
return ans;
}
例题【具体应用】
主要利用树状数组可以快速求前缀和的优势,以数据范围为下标,快速统计区间内的个数(或所需要的信息),适用于数据范围适中(一般为 \(0 \le x \le 10^6\))且需要多次求前缀和的题目。
【例题1】 三元上升子序列
【题目分析】
对于一个数 \(x\) ,计算其作为 \(j\) 时,位置在它前面比它小的数 \(x_{min}\)、位置在它后面比它大的数 \(x_{max}\),运用乘法原理的知识可知,将\(x_{min} \times x_{max}\),即可得到 \(x\) 作为 \(j\) 时的方案数 ,枚举所有 \(x\) ,即可得到总方案数。
【树状数组作用】
统计 \(x_{min}\) 和 \(x_{max}\) 时,即可将数 \(x\) 的范围作为树状数组的下标。
此时两种操作所代表的意思分别为:
\(add(x,1)\) 表示数值为 \(x\) 的数的个数 \(+1\)。
\(sum(y)\) 表示在已经扫描过的区间内,数值为从 \(1 \sim y\) 的所有数的个数。
顺序扫描序列,对于数 \(x\) ,统计两个信息。
\(r_{i,0}\) 表示位置在数 \(x\) 前面,且比它小的数。
\(r_{i,1}\) 表示位置在数 \(x\) 前面,且比它大的数。
位置在数 \(x\) 后面,且比数 \(x\) 大的数就等于:
\(所有数 - 所有位置在 x 前面比 x 小的数 - r{i,1}\)。
【code】
点击查看代码
#include<iostream>
#include<cstdio>
#include<cmath>
#define ll long long
using namespace std;
ll tree[100005],n,num;
ll r[40005][2],a[100005];
void add(ll x,ll y){
for(;x<=100005;x+=(x&-x)) tree[x]+=y;
}
ll sum(ll x){
ll ans=0;
for(;x;x-=(x&-x)) ans+=tree[x];
return ans;
}
int main(){
scanf("%lld",&n);
for(int i=1;i<=n;i++){
ll x;
scanf("%lld",&x);
a[i]=x;
num=max(num,x);
add(x,1);
r[i][0]=sum(x-1);
r[i][1]=sum(num)-sum(x);
}
ll ans=0;
for(int i=1;i<=n;i++)
ans+=r[i][0]*(sum(num)-sum(a[i])-r[i][1]);
cout<<ans<<endl;
return 0;
}
【summary】
此题算是初步认识了以数值范围为下标的树状数组的用法。下一大点求逆序对的思想与此相同。
【例题2】 [USACO04OPEN] MooFest G 加强版
【题目分析】
将奶牛按照音量从小到大进行排序,保证当前奶牛的音量一定最大,然后分类讨论所有比当前奶牛音量小的奶牛与当前奶牛的距离(坐标比当前奶牛大的和坐标比当前奶牛小的)。两者相加,乘上当前奶牛音量,枚举每个奶牛,即可得到答案。
【树状数组作用】
定义两个树状数组,都是以距离的范围作为下标, \(c\) 数组用于统计对应距离的个数,\(t\) 数组用于表示对应距离 \(\times\) 对应 距离个数的总数,通过二者,即可快速计算距离差。
【code】
计算过程的解释已在代码中注释出来。
点击查看代码
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define ll long long
using namespace std;
ll n,t[50005],c[50005];
struct A{
ll v,x;
}a[50005];
bool cmp(A xx,A yy){
if(xx.v==yy.v) return xx.x<yy.x;
return xx.v<yy.v;
}
void addc(ll x,ll y){
for(;x<=50000;x+=(x&-x)) c[x]+=y;
}
void addt(ll x,ll y){
for(;x<=50000;x+=(x&-x)) t[x]+=y;
}
ll sumc(ll x){
ll sum=0;
for(;x;x-=(x&-x)) sum+=c[x];
return sum;
}
ll sumt(ll x){
ll sum=0;
for(;x;x-=(x&-x)) sum+=t[x];
return sum;
}
int main(){
scanf("%lld",&n);
for(int i=1;i<=n;i++) scanf("%lld%lld",&a[i].v,&a[i].x);
sort(a+1,a+n+1,cmp);
ll ans=0,max_num=0;
for(int i=1;i<=n;i++){
max_num=max(max_num,a[i].x);
//以下距离之间的比较限于所有音量比当前奶牛小的奶牛。
//a[i].x*sumc(a[i].x-1) 表示当前奶牛的距离*距离比当前奶牛小的奶牛个数。
//sumt(a[i].x-1) 表示所有距离比当前奶牛小的奶牛的距离和。
//sumt(max_num)-sumt(a[i].x) 表示所有距离比当前奶牛大的奶牛的距离之和。
//sumc(max_num)-sumc(a[i].x))*a[i].x 表示当前奶牛距离 * 距离比当前奶牛大的奶牛个数
ans+=a[i].v*(a[i].x*sumc(a[i].x-1)-sumt(a[i].x-1)+(sumt(max_num)-sumt(a[i].x))-(sumc(max_num)-sumc(a[i].x))*a[i].x) ;
addc(a[i].x,1);
addt(a[i].x,a[i].x);
}
cout<<ans<<endl;
return 0;
}
【summary】
这一题的重点给到题目中树状数组 \(t\)。主要收获为:以数值范围为下标的树状数组,能够处理的信息不仅限于个数。
【例题3】P1972 [SDOI2009] HH的项链
【题意分析】
本题核心:如何判断一个区间内的贝壳是否重复?
当右端点 \(r\) 固定时,不论 \(l\) 取何值,对于任意一组重复的贝壳,都可以只统计最右端的贝壳。
原因:设一组重复贝壳中最右端的贝壳所在的位置为 \(pos_r\),那么当 \(pos_r < l\) 时,其他贝壳也不可能算进统计中,当 $pos_r \ge l $时,无论其他贝壳是否被包括,对于区间的贡献都只有 \(1\),因此,只计算最右端的贝壳即可。
因此,只需要将所有询问区间按 \(r\) 从小到大排序,计算答案即可。
【树状数组作用】
以位置为下标,每遇到一个新的数 \(num(num \le r)\),判断它是否重复,如果重复,那么将上一个相同的数的贡献值 \(-1\),将当前数的贡献值 \(+1\)。
对于一段区间 \([l,r]\),答案为 \(sum(r)-sum(l-1)\)。
【code】
点击查看代码
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
int n,m,ask_r,prev,pos;
int vis[1000005],a[1000005],t[1000005],ans[1000005];
struct A{
int l,r,num;
}ask[1000005];
bool cmp(A x,A y){
return x.r<y.r;
}
int find(int pos){
ask_r=ask[pos++].r;
while(ask_r==ask[pos].r) pos++;
return pos-1;
}
void add(int x,int y){
for(;x<=n;x+=(x&-x)) t[x]+=y;
return;
}
int sum(int x){
int su=0;
for(;x;x-=(x&-x)) su+=t[x];
return su;
}
void replace(){
for(int i=ask[prev].r+1;i<=ask_r;i++){
if(vis[a[i]]!=0) add(vis[a[i]],-1);
add(i,1);
vis[a[i]]=i;
}
for(int i=prev+1;i<=pos;i++) ans[ask[i].num]=sum(ask[i].r)-sum(ask[i].l-1);
return;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
scanf("%d",&m);
for(int i=1;i<=m;i++) scanf("%d%d",&ask[i].l,&ask[i].r),ask[i].num=i;
sort(ask+1,ask+m+1,cmp);
while(1){
if(pos==m) break;
prev=pos;
pos=find(pos+1);
replace();
}
for(int i=1;i<=m;i++) cout<<ans[i]<<endl;
return 0;
}
【\(summary\)】
此题不再以数据范围为下标,而是以位置为下标。对于树状数组的应用更加灵活。在想到以最右端的贝壳为有价值的贡献时,对应到树状数组的操作就可以是上一个重复的数的贡献值 \(-1\),当前数的贡献值 \(+1\)。然后用前缀和统计区间内的个数。算进一步的开阔思维。
求逆序对
本质上也是通过树状数组单点增加和区间求和的操作进行计算。作为一个专题单独列出来。
桶排+树状数组:
1.桶排部分:
对于一个序列 \(a\) , 我们建立一个 \(cnt\) 数组,\(cnt[x]\) 表示 \(x\) 在序列 \(a\) 中出现过的次数。当 \(a_i=val\) 时,\(cnt[val]++\)。
2.树状数组部分:
倒序扫描序列 \(a\),对于新加入的数 \(a_i\),查询 \(cnt[1~a_i-1]\) 的前缀和,并将返回的前缀和加入答案。前缀和部分就可以用树状数组来维护。
操作简单粗暴,但相当好用。
点击查看代码
for ( int i = n; i; i --) {
ans += ask (a[i] - 1);
add (a[i] , 1 );
}
【例题】
接下来通过两道题进一步了解一下逆序对的考法。(不做一下真没想到还能这样考。)
【例题1】P2448 无尽的生命
【题意简述】
看到题目显而易见是求逆序对个数。
【思路分析】
看到数据范围 \(x_i,y_i \le 2^{31}-1\),\(k \le 10^5\)。数据值域大但是个数少,且与数据之间的大小关系有关,因此考虑离散化。
离散化简单介绍
离散化实际就是一种映射,当数据值域过大而个数有限时,可以尝试离散化。
具体过程以此题为例。假设给出这么一组数据
2
123456789 123456
987654321 123456
首先将所有出现过的数收集起来,存进 \(a\) 数组,并进行排序,然后再去重保存进 \(pos\) 数组当中。

接下来就可以建立映射关系。将数值大的数在 \(num\) 数组中用数值小的数代替,但各个数之间的大小关系不变,接下来交换操作先用二分答案在 \(pos\) 数组中检索,然后通过映射在 \(num\) 数组中进行交换。

最终被交换过的数之间的逆序对在 \(num\) 数组中求即可。
被交换的数与未被交换的数之间的逆序对
考虑每个被交换的数对答案的贡献。
设 \(x<y\),当 \(x\) 和 \(y\) 交换后。
对于 \(x\) 来说, \(x \sim y\) 之间所有未被交换的数都比 \(x\) 大,形成逆序对。
对于 \(y\) 来说,\(x \sim y\) 之间所有未被交换的数都比 \(y\) 小,形成逆序对。
逆序对个数都为\(x \sim y\) 之间所有未被交换的数。
温馨提示:以下主要为代码实现讲解,本质思想同上。
对于交换过后的 \(num\) 数组,\(num_i\) 表示的是位置 \(pos_i\) 上当前所在的数在 \(num\) 数组中对应的数。记数 \(x\) 为位置 \(pos_i\) 上当前所在的数。
\(pos_{num_i}\) 表示数 \(x\) 现在所在的位置。
\(pos_i\) 表示数 \(x\) 原来在的位置。
\(\left\vert pos_i-pos_{num_i}-1\right\vert\) 表示两个位置间所有的数。
\(\left\vert num_i-i-1\right\vert\) 表示两个位置间所有被交换过的数。
因此所有未被交换的数就为 \(\left\vert pos_i-pos_{num_i}-1\right\vert - \left\vert num_i-i-1\right\vert\)。
【code】
点击查看代码
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
struct A{
int x,y;
}a[100005];
int k,pos[200005],num[200005],cnt,len;
int t[100005];
void add(int x){
for(;x<=len;x+=(x&-x)) t[x]+=1;
}
long long sum(int x){
long long ans=0;
for(;x;x-=(x&-x)) ans+=t[x];
return ans;
}
int find(int x){
int l=1,r=len;
while(l<r){
int mid=(l+r)>>1;
if(pos[mid]<x) l=mid+1;
else if(pos[mid]>x) r=mid-1;
else return mid;
}
}
int main(){
scanf("%d",&k);
for(int i=1;i<=k;i++){
scanf("%d%d",&a[i].x,&a[i].y);
num[++cnt]=a[i].x;
num[++cnt]=a[i].y;
}
sort(num+1,num+cnt+1);
for(int i=1;i<=cnt;i++){
if(num[i]==num[i-1]) continue;
pos[++len]=num[i];
}
for(int i=1;i<=len;i++) num[i]=i;
for(int i=1;i<=k;i++){
int pos1=find(a[i].x);
int pos2=find(a[i].y);
swap(num[pos1],num[pos2]);
}
long long ans=0;
for(int i=len;i>=1;i--){
add(num[i]);
ans+=sum(num[i]-1);
ans+=abs(pos[num[i]]-pos[i]-1)-abs(num[i]-i-1);
}
cout<<ans<<endl;
return 0;
}
【summary】
重点在于与未交换的数之间的求解。题目中序列的长度可以长到一个数组都存不下,但却可以用公式求呢。
【例题2】P3531 [POI2012]LIT-Letters
【题目描述】
该题的重点在于如何从题面描述转到求 \(逆序对\)。抓到重点:
-
交换 \(a\) 中相邻两个字符,求最少的交换次数。
-
\(a,b\) 中只含大写字母,且数据保证 \(a\) 可以变成 \(b\)。
对 \(b\) 串中的字符进行顺序编号(假设此时 \(b\) 中并没有重复的字母),并对应到 \(a\) 串中。
例如:
3
ABC
BCA
对 \(BCA\) 进行顺序编号,对应到 \(ABC\) 就是 \(312\)。
当序列 \(a\) 中存在数 \(a , b\),满足 $pos_a < pos_b $ , \(a > b\)。也就是形成逆序对。
而对于我们的目标,将 \(a\) 串变成 \(b\) 串,需满足任意数 \(a , b\),都有 \(pos_a < pos_b\) , \(a < b\)。
显然我们需要通过一定操作,令逆序对都消失,以达到目标。
由于题目中的交换为交换相邻的数,因此只要 \(a\) 与 \(b\) 不交换,它们之间的相对位置就不会变,也就不能达成目标。
综上所述,最少的交换次数就是逆序对的个数。
当字母重复时,我们要如何让编号对应到 \(a\) 呢?
显然逆序对个数越少越好,因此对于相同的字母,按出现的顺序进行顺序编号。代码中用单向链表实现。
【code】
点击查看代码
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#define ll long long
using namespace std;
int now[30],prev[30],nex[1000005];
char s[1000005],ss[1000005];
int a[1000005],t[1000005],lens;
void add(int x,int y){
for(;x<=lens;x+=(x&-x)) t[x]+=y;
return;
}
ll sum(int x){
ll ans=0;
for(;x;x-=(x&-x)) ans+=t[x];
return ans;
}
int main(){
scanf("%d",&lens);
cin>>(s+1);
cin>>(ss+1);
for(int i=1;i<=lens;i++){
int ch=s[i]-'A';
if(now[ch]==0) now[ch]=i;
nex[prev[ch]]=i;
prev[ch]=i;
}
for(int i=1;i<=lens;i++){
int ch=ss[i]-'A';
a[now[ch]]=i;
now[ch]=nex[now[ch]];
}
ll ans=0;
for(int i=lens;i>=1;i--){
add(a[i],1);
ans+=sum(a[i]-1);
}
cout<<ans<<endl;
return 0;
}
区间增加,单点查询
【模板】树状数组2
思路剖析
相信经过上面的头脑风暴,再来看这题已经相当简单了。
此时主要运用到差分的思想,差分是前缀和的逆运算。
当要在区间 \([x,y]\) 加上 \(k\) 时,我们进行以下操作:
\(add(x,k) , add(y+1,-k)\)
此时对于区间求前缀和对于 \(x \sim y\),它的前缀和都为 \(k\),而到 \(y+1\) ,又变成 \(0\)。此时的前缀和正好是区间增加的数,且不会对其它数产生影响。
因此,当查询第 \(x\) 个数时,只需要输出:
\(a_x(第 x 个数原本的数值) + sum(x)(变化的值)\)。
即可。
code
点击查看代码
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int a[500005],c[500005],n,m;
void add(int x,int k){
for(;x<=n;x+=x&-x) c[x]+=k;
return;
}
int q(int x){
int sum=0;
for(;x;x-=x&-x) sum+=c[x];
return sum;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=m;i++){
int type;
scanf("%d",&type);
if(type==1){
int x,y,k;
scanf("%d%d%d",&x,&y,&k);
add(x,k);
add(y+1,-k);
}
else{
int x;
scanf("%d",&x);
cout<<a[x]+q(x)<<endl;
}
}
return 0;
}